《数字信号处理》课程教学资源（习题解答）ch4 IIR数字滤波器设计

4.5MATLAB实现滤波器设计14.6习题4-1.若Butterworth滤波器的阶数由式(4-24)确定，试证明按式(4-27)确定o.的Butterworth滤波器在通带和阻带均满足技术指标。证：记p00≤03≤0Oel02(10014, -1)/2N(100.14, 1)/2NA(0;0)=101gH(j0) =101g(1+(0 /0.)2N)由上式可知，A(の;0)是关于变量/o.的单调递增函数。由课文中的推导过程可知，A(の;0)满足A(0p,0e)=Ap,A(0,0)≥As,A(0p,0)<ApA(0s,02)=As由于≤，所以0/0≤0/0el由A(;0）的单调递增特性及A(p;0el)=A,可得A(0p,0)<A,由于≤02，所以0/ 02≤ 0/ 0e3由A(0;0）的单调递增特性及A(00)=A,可得A(0,0)≥A,4-2.试利用Butterworth滤波器，设计一个满足下列条件的模拟低通滤波器。0.8≤|H(j)/≤10≤0≤5[H(jo)| ≤0.1≥10解：由题所给条件得11+(5/0, = 0.64 —→(5/0. ) * = 0.562511(10/0, ) = 0.01 —→(10/0, )* = 99N≥I(99/0.562)=3.7,取 N421g2将N=4代入由通带方程得，Q。=5/(0.5625)1/8=5.3728将N=4代入由阻带方程得，①=10/(99)/8=5.6305

4.5 MATLAB 实现滤波器设计 1 4.6 习题 4-1. 若 Butterworth 滤波器的阶数由式(4-24)确定，试证明按式(4-27)确定wc的 Butterworth 滤波器在通带和阻带均满足技术指标。 证: 记 0.1 A 1/ 2 N p c1 (10 1) p - = w w , A N s 0.1 s 1/ 2 c2 (10 -1) = w w ,wc1 £wc3 £wc2 ( ) N A H 2 c 2 c (w;w ) =10lg (jw) =10lg 1+ (w /w ) 由上式可知，A(w ;wc )是关于变量w /wc的单调递增函数。由课文中的推导过程可知，A(w ;wc ) 满足 A(wp ;wc1)=Ap，A(ws ;wc1)³ As，A(wp ;wc2)£Ap，A(ws ;wc2)= As 由于wc1£ wc3，所以 wp / wc3£ wp / wc1 由 A(w ;wc ) 的单调递增特性及 A(wp ;wc1)=Ap可得 A(wp ;wc3)£Ap 由于wc3£ wc2，所以 ws / wc2£ ws / wc3 由 A(w ;wc ) 的单调递增特性及 A(ws ;wc2)=As可得 A(ws ;wc3)³As 4-2. 试利用 Butterworth 滤波器，设计一个满足下列条件的模拟低通滤波器。 0.8 £ H(jw) £ 1 0 £ w £ 5 H(jw) £ 0.1 w ³ 10 解： 由题所给条件得 0.64 1 (5/ ) 1 2 = + N wc (5/ ) 0.5625 2 ¾® = N wc 0.01 1 (10 / ) 1 2 = + N wc (10 / ) 99 2 ¾® = N wc 3.7 2lg 2 lg(99 / 0.5625) N ³ = , 取 N=4; 将 N=4 代入由通带方程得， 5/(0.5625) 5.3728 1/ 8 wc = = 将 N=4 代入由阻带方程得， 10 /(99) 5.6305 1/ 8 wc = =

H(s) =((s/@)2+0.7654(s/@)+1)(s/@)2+1.8478(s/o)+1)由0=5.3728得出的系统为833.3025H(s) =(s2+4.1123s + 28.867)(s2 + 9.9279s+28.867)由@。=5.6305得出的系统为1005.1H(s)=(s2 + 4.3096s + 31.7025)(s +10.404s +31.7025)4-3.试用ChebyshevI型滤波器，重做题4-2。解：由题所给条件得1 /1/0.01-1)arccosh(c0。=5,=V1/0.82-1=0.75N~2.5arccosh(10/5)取 N=3; β= sinh"(/e) =0.3662,N元元, =-sinh(β)sin -=-0.1872, O, =-cosh(β)cos--0.92742N2N(o, +0))sinh(β)H(s) =(s/5)+sinh(β) ~ (s/5)2-2o,(s/5)+(α +0)41.666741.6667(s +1.8722)(s2 +1.8722s +22.2552)s3+3.7444s2+25.7604s+41.66674-4.已知H(s)为CBI型低通滤波器，且N=3,0=3,0=10,8=0.01该滤波器在阻带正好满足指标。试确定用实系数有理多项式表示的H(s)。解：(1)由通带截频の,确定の0,=0,=3(2)由阻带波动确定s由-821+"cosha(N arccosh(o, /o,))得

(( / ) 0.7654( / ) 1)(( / ) 1.8478( / ) 1) 1 ( ) 2 2 + + + + = c c c c s s s s H s w w w w 由 = 5.3728 wc 得出的系统为 ( 4.1123 28.867)( 9.9279 28.867) 833.3025 ( ) 2 2 + + + + = s s s s H s 由 = 5.6305 wc 得出的系统为 ( 4.3096 31.7025)( 10.404 31.7025) 1005.1 ( ) 2 2 + + + + = s s s s H s 4-3. 试用 Chebyshev I 型滤波器，重做题4-2。 解： 由题所给条件得 = 5 wc , 1/ 0.8 1 0.75 2 e = - = , 2.5 arccosh(10 / 5) 1/ 0.01 1) 1 arccosh( » - = e N , 取 N=3; 0.3662 sinh (1/ ) 1 = = - N e b , 0.1872 2 sinh( )sin 1 = - = - N p s b , 0.9274 2 cosh( ) cos 1 = - = - N p w b ( / 5) 2 ( / 5) ( ) ( ) ( / 5) sinh( ) sinh( ) ( ) 2 2 2 2 2 k k k k k s s s H s s s w s w b b - + + + ´ + = ( 1.8722)( 1.8722 22.2552) 41.6667 2 + + + = s s s 3.7444 25.7604 41.6667 41.6667 3 2 + + + = s s s 4-4. 已知 H(s)为 CB I 型低通滤波器，且 N=3，wp=3，ws=10，ds=0.01 该滤波器在阻带正好满足指标。试确定用实系数有理多项式表示的 H(s)。 解： (1)由通带截频wp确定wc wc =wp=3 (2)由阻带波动确定e 由 2 s p 2 2 1 cosh ( arccosh( / )) 1 s N d e w w = + 得

4.5MATLAB实现滤波器设计3/1/82-1=0.72386cosh(Narccosh(, /o,)(3)(o° +0)o sinh(β)H(s)=s+0 sinh(β)s?-20,0.s+0.(o) +0,)(2k -1)p@, =-cosh(B)cos(2k-1)Parcsinh(1/)B=o,=-sinh(β)sinN2N2N9.3255H(s)=s3+2.3078s2+9.4131s+9.32558=0.8101,8=0.01,4-5.已知二阶CBIⅡI型低通滤波器的参数ε=0.1，且HG1)=0。试求用实系数有理多项式表示的 H(s)。gC,(o. /0)解：由H(jo)"=C,(x)=2x2-1,得：0,=1//21+°c2(0 /0), β=arcsinh(1/e)S, =0, + jo, 0, =-sinh(β)sin ",, 0, =-cosh(β)cos",N1p, =1/ s,=0.2993 +j0.3308, =, = j/cos(p/4)=+ j 1.4142( /(s?+)0.0995(s2+1)H(s)=(s2-2@.Relp,/s+@2/p/)s2+0.4233s+0.09954-6.试利用Butterworth滤波器设计一个通带3dB截频の=5rad/s的三阶模拟高通滤波器。解：变换Hp(s)= Hμp(3) =1/ s要求的低通滤波器的3dB截频为可=1/o=1/53dB截频为の，=1/5的3阶巴特沃思滤波器为1Hμ(s) =(5s + 1)(25s2 + 5s +1)高通滤波器为s3Hp(s) =(s+5)(s2 +5s+25)

4.5 MATLAB 实现滤波器设计 3 cosh( arccosh( / )) 1/ 1 s p 2 s w w d e N - = =0.7238 (3) 2 ( ) ( ) sinh( ) sinh( ) ( ) 2 1 2 1 2 1 c c 2 2 1 2 1 c 3 c s w w s w s w w b w b - + + + ´ + = s s s H s N k k 2 (2 1)p sinh( )sin - s = - b , N k k 2 (2 1)p cosh( ) cos - w = - b , N arcsin h(1/ e ) b = 2.3078 9.4131 9.3255 9.3255 ( ) 3 2 + + + = s s s H s ds=0.8101, ds=0.01, 4-5. 已知二阶 CB II 型低通滤波器的参数e=0.1，且 H(j1)=0。试求用实系数有理多项式 表示的 H(s)。 解：由 1 ( / ) ( / ) (j ) c 2 2 2 c 2 2 2 2 e w w e w w w C C H + = , ( ) 2 1 2 C2 x = x - , 得: =1/ 2 wc 1 1 1 s = s + jw , 4 sinh( )sin 1 p s = - b , 4 cosh( ) cos 1 p w = - b , N arcsin h(1/ e ) b = 1 1 p =1/s = -0.2993 + j0.3308, j/ cos(p/4) z1 = = + j 1.4142 ( 2 Re{ } ) ( )( ) ( ) 2 2 c c 2 2 2 c 2 2 2 k k k k k s p s p p z s z H s w w w - + + = 0.4233 0.0995 0.0995( 1) 2 2 + + + = s s s 4-6. 试利用 Butterworth 滤波器设计一个通带 3dB 截频wp = 5 rad/s 的三阶模拟高通滤波 器。 解：变换 H s H s s s HP LP ( ) = ( ) = 1/ 要求的低通滤波器的 3dB 截频为 = 1/ = 1/ 5 wp wp 3dB 截频为 = 1/ 5 w p 的 3 阶巴特沃思滤波器为 (5 1)(25 5 1) 1 ( ) 2 + + + = s s s H s LP 高通滤波器为 ( 5)( 5 25) ( ) 2 3 + + + = s s s s H s HP

直接计算幅度响应的模方，证明4-7.BsHep(s) =$?+Bs+0是一个中心频率为の(Hβ(jo。)=1)，通带3dB带宽为B的带通滤波器。B"o?解：[H p(jo)" =(0*-0)+B?由上式知HBp(jo)≤1。在の)=±の。时HBp(jo)达到最大值1。所以HBp(jo.)=1。由HBp(jo)=1/2得(0 -0)) = B'0?0-Bo-0. =0当>0,00时B?B1所以02=号++0,0>0,00,0>0时02-Bo-0, =0B2B 所以+00p2=420>0,0 <0.时0?+B0-0,=0

4-7. 直接计算幅度响应的模方，证明 2 0 BP 2 ( ) + +w = s Bs Bs H s 是一个中心频率为w0 ( (j ) 1 HBP w0 = )，通带 3dB 带宽为 B 的带通滤波器。 解： 2 2 2 2 0 2 2 2 2 ( ) ( ) w w w w w B B H j BP - + = 由上式知 ( ) 1 2 HBP jw £ 。 在 w = ±w0 时 2 H ( jw) BP 达到最大值 1 。 所 以 ( ) 1 HBP jw0 = 。 由 ( ) 1/ 2 2 HBP jw = 得 2 2 2 2 0 2 (w -w ) = B w 当 0 w > 0,w > w 时 0 2 0 2 w - Bw -w = 所以 2 0 2 2 2 4 w = + +w B B p 0 w > 0,w 0,w > w 时 0 2 0 2 w - Bw -w = 所以 2 0 2 2 2 4 w = + +w B B p 0 w > 0,w < w 时 0 2 0 2 w + Bw -w =

4.5MATLAB实现滤波器设计5B2B+0?OpI=2V4所以A03=0p2-0=B4-9.已知一模拟低通滤波器的技术指标为：f=2.1kHz,f=8kHz,A,=0.5dB,A,=30dB试分别确定用Butterworth滤波器和CBI型滤波器实现该指标所需的阶数。解：(1)Butterworth滤波器由式(4-24)可得100.14,Ig(100.14N≥~3.3721g(0./0,)取Ngw=4。(2)CBI型滤波器由式(4-38)得= /100-14, -1=0.3493由式(4-39)得arccosh(- /10014 -1)8N≥=2.58arccosh(o,/o,)取NcB=3。4-10.利用二阶归一化Butterworth低通滤波器，设计一个中心频率为の。=20rad/s，通带3dB带宽为B=4rad/s的模拟带通滤波器。解：(1)变换中的参数为B=4，の。=20(2）2阶归一巴特沃思低通滤波器为1Hto(s)=s2 + /2s+1B"s?s?+0.(3) Hμp(s) = Hr(3)s :Bs(s? +0.)* + ~/2Bs(s? +0)+(Bs)B°s?s*+V2Bs+(20+B2)s2+/2B0s+0

4.5 MATLAB 实现滤波器设计 5 2 0 2 1 2 4 w = - + +w B B p 所以 Dw3dB =wp 2 -wp1 = B 4-9. 已知一模拟低通滤波器的技术指标为： fp=2.1 kHz，fs=8 kHz, Ap=0.5 dB, As=30 dB 试分别确定用 Butterworth 滤波器和 CB I 型滤波器实现该指标所需的阶数。 解： (1) Butterworth 滤波器 由式(4-24)可得 3.37 2lg( / ) ) 10 1 10 1 lg( p s 0.1 0.1 s p » - - ³ w w A A N 取NBW=4。 (2) CB I型滤波器 由式(4-38)得 10 1 p 0.1 = - A e =0.3493 由式(4-39)得 2.58 arccosh( / ) 10 1) 1 arccosh( s p 0.1 s » - ³ w w e A N 取NCB=3。 4-10. 利用二阶归一化 Butterworth 低通滤波器，设计一个中心频率为 20 w0 = rad/s，通带 3dB 带宽为 B=4 rad/s 的模拟带通滤波器。 解： (1)变换中的参数为 B = 4， 20 w0 = (2) 2 阶归一巴特沃思低通滤波器为 2 1 1 ( ) 2 0 + + = s s H s L (3) Bs s H s H s s BP L 2 0 2 0 ( ) ( ) +w = = 2 2 0 2 2 2 0 2 2 2 (s ) 2Bs(s ) (Bs) B s + + + + = w w 4 0 2 0 2 2 2 0 4 3 2 2 + 2 + (2w + ) + 2 w +w = s Bs B s B s B s

16s2s*+5.6569s+816s2+2262.7s+1600004-11.有人提出了以下一种设计模拟带阻滤波器的方法：(1)由B=p2-p，=p确定变换参数。(2)原型低通滤波器的阻带截频の为,=minoBos!BOs2其中0=-0.,+0.-02+0.(3)设计通带截频为1(rad/s)、阻带截频为の、通带衰减为Ap、阻带衰减为A,的原型低通滤波器H.(3)。(4）由式(4-74)获得带阻滤波器用上述步骤重做例4-17，画滤波器的幅度响应曲线。分析和讨论所出现的问题。A,=1dB,A,=10 dB,0pr=6 rad/s,Op2=13 rad/s,0=9rad/s,=11 rad/s解：(1)带阻变换中的参数为B=Op2-Op=7,0=/oplOp2=8.8318(2)由Bos!Bo,2-21，可1.79070=-01 +0.-0,2 +0?得=min=1.7907(3)由[N,wc]=buttord(l,ws bar,Ap,As,'s');[num,den]=butter(N,wc,"s);得原型低通滤波器的分子多项式系数num与分母多项式系数den分别为000num =[03.4274]den=[1.00003.55556.32086.58243.4274](4)由[numt,dent] = Ip2bs(num,den,w0,B);得带阻滤波器分子多项式系数numt与分母多项式系数dent分别为numt-[1.0000e+0001.7830e-0143.1200e+0023.6258e-0123.6504e+0042.3634e-0101.8982e+0064.6565e-0093.7015e+007]3.5016e+00335.1302e+004dent=[1.0000e+0001.3444e+0014.0237e+0022.7313e+0052.4480e+0066.3797e+0063.7015e+007]下画出了该滤波器的增益响应响应曲线。由图可知，所设计的滤波器也满足设计指标。但该方法存在以下不足：

5.6569 816 2262.7 160000 16 4 3 2 2 + + + + = s s s s s 4-11. 有人提出了以下一种设计模拟带阻滤波器的方法： (1)由 B = wp2 -wp1， p1 p2 2 w0 = w w 确定变换参数。 (2)原型低通滤波器的阻带截频ws 为 min{ , } ws = ws1 ws2 其中 2 0 2 s1 s1 1 w w w w - + = B s ， 2 0 2 s 2 s 2 2 w w w w - + = B s (3)设计通带截频为 1 (rad/s)、阻带截频为ws 、通带衰减为 Ap、阻带衰减为 As的原 型低通滤波器 ( ) L H s 。 (4) 由式(4-74)获得带阻滤波器. 用上述步骤重做例 4-17，画滤波器的幅度响应曲线。分析和讨论所出现的问题。 Ap=1dB，As=10 dB，wp1=6 rad/s，wp2=13 rad/s，ws1=9 rad/s，ws2=11 rad/s 解： (1)带阻变换中的参数为 7 B =wp 2 -wp1 = ， 8.8318 w0 = wp1wp 2 = (2)由 21 2 0 2 s1 s1 1 = - - + = w w w w B s ， 1.7907 2 0 2 s 2 s 2 2 = - - + = w w w w B s 得 min{ , } 1.7907 ws = ws1 ws2 = (3)由 [N,wc]=buttord(1,ws bar,Ap,As,'s'); [num,den]=butter(N,wc,'s'); 得原型低通滤波器的分子多项式系数 num 与分母多项式系数 den 分别为 num =[0 0 0 0 3.4274] den =[1.0000 3.5555 6.3208 6.5824 3.4274] (4)由 [numt,dent] = lp2bs(num,den,w0,B); 得带阻滤波器分子多项式系数 numt 与分母多项式系数 dent 分别为 numt=[1.0000e+000 1.7830e-014 3.1200e+002 3.6258e-012 3.6504e+004 2.3634e-010 1.8982e+006 4.6565e-009 3.7015e+007] dent=[1.0000e+000 1.3444e+001 4.0237e+002 3.5016e+003 5.1302e+004 2.7313e+005 2.4480e+006 6.3797e+006 3.7015e+007] 下画出了该滤波器的增益响应响应曲线。由图可知，所设计的滤波器也满足设计指标。 但该方法存在以下不足：

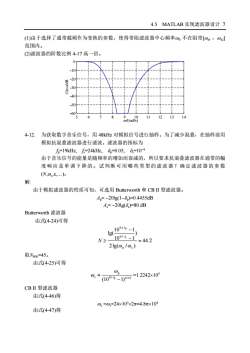
4.5MATLAB实现滤波器设计7(1)由于选择了通带截频作为变换的参数，使得带阻滤波器中心频率0。不在阻带[01，0]范围内。(2)滤波器的阶数比例4-17高一倍。0-1020-30050-6078111314569/radl)12为获取数字音乐信号，用48kHz对模拟信号进行抽样。为了减少混叠，在抽样前用4-12.模拟抗混叠滤波器进行滤波。滤波器的指标为f=19kHz，=24kHz,8=0.05，8=10-由于音乐信号的能量是随频率的增加而衰减的，所以要求抗混叠滤波器在通带的幅度响应是单调下降的。试判断可用哪些类型的滤波器？确定滤波器的参数(N,.,6,..).解:由于模拟滤波器的性质可知，可选用Butterworth和CBII型滤波器。A,=-201g(1-8,)=0.4455dBA,=-20lg(8)=80 dBButterworth滤波器由式(4-24)可得100.1Ig(100.14,N≥44.221g(0, /0,)取Ngw=45。由式(4-25)可得op=1.2242×1050(100.14, 1)/2NCBII型滤波器由式(4-46)得0。=0,=24×103×2元=4.8元×104由式(4-47)得

4.5 MATLAB 实现滤波器设计 7 (1)由于选择了通带截频作为变换的参数，使得带阻滤波器中心频率w0 不在阻带[ws1 ，ws2] 范围内。 (2)滤波器的阶数比例 4-17 高一倍。 5 6 7 8 9 10 11 12 13 14 -60 -50 -40 -30 -20 -10 0 w/(rad/s) G(w)/dB 4-12. 为获取数字音乐信号，用 48kHz 对模拟信号进行抽样。为了减少混叠，在抽样前用 模拟抗混叠滤波器进行滤波。滤波器的指标为 fp=19kHz, fs=24kHz, dp=0.05, ds=10-4 由于音乐信号的能量是随频率的增加而衰减的，所以要求抗混叠滤波器在通带的幅 度响应是单调下降的。试判断可用哪些类型的滤波器？确定滤波器的参数 (N,wc ,e,¼)。 解: 由于模拟滤波器的性质可知，可选用 Butterworth 和 CB II 型滤波器。 Ap= -20lg(1-dp )=0.4455dB As= -20lg(ds )=80 dB Butterworth 滤波器 由式(4-24)可得 44.2 2lg( / ) ) 10 1 10 1 lg( p s 0.1 0.1 s p » - - ³ w w A A N 取NBW=45。 由式(4-25)可得 0.1A 1/ 2N p c (10 1) p - = w w =1.2242´105 CB II 型滤波器 由式(4-46)得 wc =ws=24´103´2p=4.8p´104 由式(4-47)得

-10-2V100.14-1由式(4-48)得1arccosh(V10014,-可得N≥~15.5arccosh(o, /o,)取NcB=16。4-13.利用脉冲响应不变法，将下列模拟滤波器转换为数字滤波器。2(I) H,(s) =(s+ β)~ + 22s+β(2) H, (s) =(s + β)* + 22Cs + D(3) H,(s) =(s + β)* + 22解：入1(1)(s + β) + 22s+β-jas+β+ja2i1Te-T sin(2T)z-I1TH,(=)=2j(1-e-(β+ja)T_-I1-e-(B-ja)r12e-T cos(2T)-l +e-2Pr _-211s+β1(2)(s + β)2 + 2221s+β-jas+β+jaT[1-e-B cos(aT)-111H.(z)e-(β+ja)T_-I1-e-(β-ju)T.1-2e-BT cos(^T)=" +e-2βT_-22C(s+β)+(D-βC)H,(s)=(3)(s + β)? + 22H,(2) =CH,(z)+[(D- βC) / 2JH,(2)TC+Te-βBr (D-βC)/a ]sin(aT)-Ccos(aT))=-1-2e-BTcos(αT)=-l +e-2B=-24-14.利用脉冲响应不变法，将下列模拟滤波器转换为数字滤波器。设T=1sS+2(1) H,(s) =(s + I)(s + 3)$+1(2) H,(s) =(s +0.1)* + 9

10 1 1 s 0.1 - = A e =10-4 由式(4-48)得 可得 15.5 arccosh( / ) ) 10 1 1 arccosh( s p 0.1 p » - ³ w w e A N 取NCB=16。 4-13. 利用脉冲响应不变法，将下列模拟滤波器转换为数字滤波器。 (1) 1 2 2 ( ) ( ) b l l + + = s H s (2) 2 2 2 ( ) ( ) b l b + + + = s s H s (3) 3 2 2 ( ) ( ) + b + l + = s Cs D H s 解： (1) ÷ ÷ ø ö ç ç è æ + + - + - = + b + l b l b l l s j s j s j 1 1 2 1 ( ) 2 2 ÷ ÷ ø ö ç ç è æ - - - = -( + ) -1 -( - ) -1 1 1 1 1 1 2 ( ) j e z e z T H z b jl T b jl T 1 2 2 1 1 2 cos( ) sin( ) - - - - - - - + = e T z e z Te T z T T T b b b l l (2) ÷ ÷ ø ö ç ç è æ + + + + - = + + + b l b l b l b s s j s j s 1 1 2 1 ( ) 2 2 ÷ ÷ ø ö ç ç è æ - + - = -( + ) -1 -( - ) -1 2 1 1 1 1 2 ( ) e z e z T H z b jl T b jl T [ ] 1 2 2 1 1 2 cos( ) 1 cos( ) - - - - - - - + - = e T z e z T e T z T T T b b b l l (3) 3 2 2 ( ) ( ) ( ) ( ) b l b b + + + + - = s C s D C H s ( ) ( ) [( )/ ] ( ) 3 2 1 H z = CH z + D - bC l H z {[ ] } 1 2 2 1 1 2e cos( ) e e ( ) / sin( ) cos( ) - - - - - - - + + - - = T z z TC T D C T C T z T T T b b b l b l l l 4-14. 利用脉冲响应不变法，将下列模拟滤波器转换为数字滤波器。设 T=1s。 (1) ( 1)( 3) 2 ( ) 1 + + + = s s s H s (2) ( 0.1) 9 1 ( ) 2 2 + + + = s s H s

4.5MATLAB实现滤波器设计93s2 + 4(3) H,(s) =(s+2)(s2 +s+5/4)解：0.50.5H,(s)=(1)S+3S + 10.50.51-0.2088--H,(2)=1-e-l_-l1-e-3_-110.4177=- +0.0183--2(2)由题4-13(2)结论可得1 + 0.9341z-1 + e-0 (0.3 sin(3) cos(3)) =-1H,(=)=1 2e-01 cos(3)-- + e-0.2,-21+1.79162- +0.81872-2(3)64/13(-25/13)s-14/1364/13(-25/13)s-14/13H,(s)=$? +s+5/4$+2$+2(s+1/2)° +1由题4-13(3)结论可得64/13(-25/13)+e-0.5 (-3/26)|sin(1)+(25/13)cos(1))=-1H,(=)=1-e---1-2e-0.5 cos(1)--l +e_-24.9231-1.9231+0.5713210.6554z +0.36792-21-0.1353z-3-2.3951-+1.7338=-210.7908- +0.4566z20.0498≥34-15.利用模拟Butterworth低通滤波器和脉冲响应不变法，设计一个满足下列条件的数字滤波器。1/ /2 ≤|H(ej0)|≤10≤Q≤0.2p[H(ein)≤0.20.6元≤Q≤p解：取T=11)则模拟滤波器指标为0,=0.2元，0,=0.6元2)设计模拟滤波器的由于，是3db截频，所以の。=0。=0.2元。由阻带指标得11+(0.6 /0.2 ) = 0.04 ~ (3)* = 24 ± ≥1:(24)/21g3=1.45取N=2，所以

4.5 MATLAB 实现滤波器设计 9 (3) ( 2)( 5/ 4) 3 4 ( ) 2 2 3 + + + + = s s s s H s 解： (1) 3 0.5 1 0.5 ( ) 1 + + + = s s H s 1 1 3 1 1 1 e 0.5 1 e 0.5 ( ) - - - - - + - = z z H z 1 2 1 1 0.4177 0.0183 1 0.2088 - - - - + - = z z z (2)由题 4-13(2)结论可得 0.1 1 0.2 2 0.1 1 2 1 2e cos(3) e 1 e {0.3sin(3) cos(3)} ( ) - - - - - - - + + - = z z z H z 1 2 1 1 1.7916 0.8187 1 0.9341 - - - + + + = z z z (3) 5/ 4 ( 25/13) 14 /13 2 64 /13 ( ) 2 3 + + - - + + = s s s s H s ( 1/ 2) 1 ( 25/13) 14 /13 2 64 /13 2 + + - - + + = s s s 由题 4-13(3)结论可得 {[ ] } 0.5 1 1 2 0.5 1 2 1 3 1 2e cos(1) e ( 25/13) e ( 3/ 26) sin(1) (25/13) cos(1) 1 e 64 /13 ( ) - - - - - - - - - + - + - + + - = z z z z H z 1 2 1 1 1 0.6554 0.3679 1.9231 0.5713 1 0.1353 4.9231 - - - - - + - + + - = z z z z 1 2 3 1 2 1 0.7908 0.4566 0.0498 3 2.3951 1.7338 - - - - - - + - - + = z z z z z 4-15. 利用模拟 Butterworth 低通滤波器和脉冲响应不变法，设计一个满足下列条件的数 字滤波器。 1/ 2 (e ) 1 0 0.2p j £ £ £ W £ W H (e ) 0.2 0.6 p j £ p £ W £ W H 解：取 T=1 1)则模拟滤波器指标为 w p = 0.2p ，ws = 0.6p 2)设计模拟滤波器的 由于wp 是 3db 截频，所以wc = wp = 0.2p 。由阻带指标得 0.04 1 (0.6 / 0.2 ) 1 2 = + N p p (3) 24 2 ® = N N ³ lg(24)/ 2lg3 =1.45 取 N=2，所以

10.39480.4443H(s) :=0.8886(s + 0.4443)* + 0.44432(s/@)2+/2(s/@)+1s2+0.8886s+0.39483）将模拟滤波器转换为数字滤波器由题4-13(1)的结果得0.2449z~1e-0443 sin(0.4443)--lH()=0.888611.1580-- +0.41122-212e-.443 co(0.4443)- +e-08864-16.利用Chebvshevl型滤波器，重做题4-15。解：取7=1(1)则模拟滤波器指标为0，=0.2元，0，=0.6元(2)由通带截频,确定。0。=0,=0.2元(3)确定81由1+22可得=1(3)阻带指标确定N由1=831+cosh(Narccosh(o,/0,)可得/1/82-1)arccosh(-N≥arccosh(o,/o.)N=1.2887，取N=2(4)设计AFβ= aresinh(/a) =0.407NS, =-sinh(β)sin(p/4)- jcosh(β)cos(/4)=-0.3218-j0.77690.s10.1974H(s)=1+82 52-20,0.s+0-1s.]?s2+0.4044s+0.27920.1594z~1(5) H(=)=11.44312 + 0.6674=-2

0.8886 0.3948 0.3948 ( / ) 2( / ) 1 1 ( ) 2 2 + + = + + = s s s s H s wc wc 2 2 ( 0.4443) 0.4443 0.4443 0.8886 + + = s 3) 将模拟滤波器转换为数字滤波器 由题 4-13(1)的结果得 0.4443 1 0.8886 2 0.4443 1 1 2 cos(0.4443) sin(0.4443) ( ) 0.8886 - - - - - - - + = e z e z e z H z 1 2 1 1 1.1580 0.4112 0.2449 - - - - + = z z z 4-16. 利用 ChebyshevI 型滤波器，重做题4-15。 解：取 T=1 (1)则模拟滤波器指标为 w p = 0.2p ，ws = 0.6p (2)由通带截频wp确定wc wc =wp=0.2p (3)确定e 由 2 1 1 1 2 = + e 可得 e = 1 (3)阻带指标确定 N 由 2 s p 2 2 1 cosh ( arccosh( / )) 1 s N d e w w = + 可得 arccosh( / ) 1/ 1) 1 arccosh( s p 2 w w d e - ³ s N N=1.2887, 取 N=2 (4)设计 AF 0.4407 arcsinh(1/ ) = = N e b sinh( )sin(p/4) jcosh( )cos( /4) 0.3218 j0.7769 s1 = - b - b p = - - 2 1 2 1 c c 2 2 1 2 c 2 1 2 1 ( ) s s s s H s s w w w + e - + = 0.4044 0.2792 0.1974 2 + + = s s (5) 1 2 1 1 1.4431 0.6674 0.1594 ( ) - - - - + = z z z H z