《数字信号处理》课程教学课件（PPT讲稿）ch2_2 DFT性质

离散傅里叶变换的性质1.线性DFT (ax,[k] + bx2[k]}= aDFT (x[k]})+ bDFT (x2[k])需将较短序列补零后，再按长序列的点数做DFT2.循环位移（Circularshiftof a sequence）循环位移定义为y[k] = x[(k +n)~]R[k]

离散傅里叶变换的性质 1. 线性 DFTax1 [k]+ bx2 [k]= aDFTx1 [k]+ bDFTx2 [k] 需将较短序列补零后，再按长序列的点数做DFT 2. 循环位移(Circular shift of a sequence) y[k] x[(k n) ]R [k] = + N N 循环位移定义为

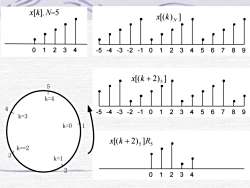
x[K], N=5x[(k)n ]32402856720295.3-1475k=445678O230k=3k=0x[(k + 2)s]Rk==2k=102732

x[k], N=5 0 1 2 3 4 [( ) ] N x k -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 [( 2) ] + 5 x k -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 5 5 x[(k + 2) ]R 0 1 2 3 4 1 5 4 3 2 k=0 k==2 k=1 k=4 k=3

DFT时域循环位移特性·DFS(x[k + n]} = W-mn X[m]DFT(x[(k +n)]R[K])= Wmn X[m]DFT频域循环位移特性. DFS(Wkx[k] = X[m + ]]DFT(wkx[K]= X[(m+ 1) JR[m]

[ ] ~ [ ]} ~ DFS{x k n W X m mn N − • + = DFTx[(k n) ]R [k] W X[m] mn N N N − + = [ ] ~ [ ]} ~ DFS{W x k X m l lk • N = + DFTW x[k] X[(m l) ]R [m] N N l k N = + DFT时域循环位移特性 DFT频域循环位移特性

3.对称性（symmetry）周期共轭对称(Periodic conjugate symmetry)定义为x[k] = x*[(-k)~]R~[k] = x*[N -k]周期共轭反对称(Periodic conjugate antisymmetry)定义为x[k] = -x*[(-k)~]R[k] = -x *[N - k]当序列x[K为实序列时，周期偶对称序列满足x[k] = x[N -k]当序列x[K为实序列时，周期奇对称序列满足x[k] =-x[N -k]

3. 对称性(symmetry) 周期共轭对称(Periodic conjugate symmetry)定义为 周期共轭反对称(Periodic conjugate antisymmetry)定义为 x[k] x*[( k) ]R [k] x*[N k] = − N N = − x[k] x*[( k) ]R [k] x*[N k] = − − N N = − − 当序列x[k]为实序列时，周期偶对称序列满足 x[k] = x[N − k] 当序列x[k]为实序列时，周期奇对称序列满足 x[k] = −x[N − k]

对称特性·DFS(x*[k]} = X*[-m]1DFT(x*[k]} = X*[(-m)]R[m]·DFS[x*[-k]} = X*[m]1DFT(x*[(-k)]R~[k]} = X*[m]当x[k]是实序列时X[m] = X*[(-m) ]R[k]

对称特性 [ ] ~ [ ]} ~ • DFS{x k = X −m   [ ] ~ [ ]} ~ DFS{x k X m   • − = [ ] ~ DFT{x [( k) N ]RN [k]} X m   − = DFT{x [k]} X [( m) ]R [m] = − N N   当x[k]是实序列时 X[m] X [( m) ]R [k] = − N N 

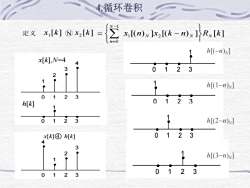
4.循环卷积2定义 x,[k] x,[]x,[(n)n]x2[(k - n)n1|Rn[k]n=0h[(-n)N]1x[k],N=4401233211h[(1-n)N]r02312301h[k]1T11o231h[(2-n)N]0123x[K]④ h[k]4312h[(3-n)N]1?03210231

4.循环卷积 定义 [ ] 1 x k N [ ] 2 x k [( ) ] [( ) ] [ ] 1 2 1 0 x n x k n R k N N N N n       =  − − = x[k],N=4 0 1 2 3 1 2 3 4 h[k] 0 1 2 3 1 0 1 2 3 1 0 1 2 3 1 0 1 2 3 1 0 1 2 3 1 x[k] 4 h[k] 0 1 2 3 4 1 2 3 h[(−n)N ] h[(1−n)N] h[(2−n)N ] h[(3−n)N]

卷积定理DFT (x[k]x2[k]}= X[m]X,[m]DFT(x,[k]x[k]]= 一 X,[m] X,[m]N

卷积定理 DFT [ ] [ ] [ ] [ ] x1 k N x2 k = X1 m X2 m   [ ] [ ] 1 DFT [ ] [ ] 1 2 X1 m N X2 m N x k x k =

序列DFT与Z变换的关系N-12元N-1kmZ2Nx[k]zX[m] = X(zx[k]e一= 2元mmNk=0z=ek=0-=ex[K]的 X[m]等于其z变换X(2)在单位圆上等间隔取样jIm(z)Z平面元2元mN211Re(z)12元(N-1)N单位圆

序列DFT与z变换的关系 Re(z) jIm(z) N 2 m N 2 0 z平面 ( 1) 2 N − N  单位圆 -1 1 j -j m N j z e m N j k N z e k X m X z x k z   2 2 [ ] ( ) [ ] | 1 0 = − − = = = =  km N N k x k e 2 -j 1 0  [ ] − = = x[k]的 X[m]等于其z变换X(z)在单位圆上等间隔取样

设序列x/kl的长度为NN-1X()-2x[k]w.mX[m] =2x[k]z-kk=0k=0X[m] = X(z)2元 . ;m = 0,1...N - 1Nz=eZ变换IDFT→ X(z)X[m]x[k]AYX[m](1- zX(z)（内插公式）7-z-lWrmNm=(

设序列x[k]的长度为N k N k X z x k z − − = ( ) =  [ ] 1 0 km N N k X[m] x[k]W 1 0  − = = [ ] = ( ) 2 ; = 0,1 −1 = X m X z m N m N j z e   X[m] ⎯IDFT ⎯⎯→ x[k] ⎯Z⎯变换⎯→ X (z) m N N m N z W X m N z X z − − − = − − − =  1 1 0 1 (1 ) [ ] ( ) (内插公式)