《数字信号处理》课程教学课件（PPT讲稿）ch1_3 DTFT

离散时间Fourier变换(DTFT)·DTFT的定义·DTFT性质·DTFT的频域抽样用MATLAB计算DTFT

•DTFT的定义 •DTFT性质 •DTFT的频域抽样 •用MATLAB计算DTFT 离散时间Fourier变换(DTFT)

DTFT的定义80x[k]e-jkDTFT:X(ej°)=k=-00特点：1)X(e J?)是连续的2)X(e j2)是周期为2元的周期函数IDTFT:X(ej")ejk?d?x[k] 2元2元ojd(22)) = Xr(ej?)+ jX,(ej°)X(ej°)=d(②) 的主值(principal value)一元<(2)<≤元

DTFT的定义 特点：1)X(e jW )是连续的 2)X(e jW )是周期为2p的周期函数 IDTFT: W p W W p x k X e e d j jk ( ) 2 1 [ ] 2  = ( ) ( ) ( ) ( ) W W (W) W jW I j R j j j X e = X e e = X e + j X e (W) 的主值(principal value) -p(W)p j k k j X e x k e W - W  =- DTFT: ( ) =  [ ]

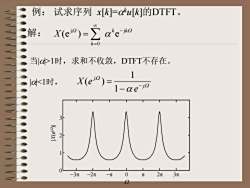
例：试求序列 x[K]=αtu[K]的DTFT。X(ei°)= αhe-ik?解：k=0当|α>1时，求和不收敛，DTFT不存在。1X(ej")[α<1时,l-αe-j?3EM0-3元-2元2元3元元一元2

例： 试求序列 x[k]=aku[k]的DTFT。 W W a k k k X j 0 j (e ) e -  = = 当|a|>1时，求和不收敛，DTFT不存在。 |a|<1时， W W a j j e X e - - = 1 1 ( ) 0 3p 0 1 2 3 -3p -2p -p p 2p |X(ejW )| W 解：

DTFT的收敛性x[k]e-j2k定义X(eig)的部分和 X(ej)=k=-N若Z [x[k]Λ8k则 lim|X(ej°)-X(ei°) =0N-00Z [x[k]若<8则 lim " X(ei°)-X(ej°) d2=0N-00

DTFT的收敛性 定义X(ejW)的部分和 k N k N N X x k jW jW (e ) [ ]e - =- =   x[k]   k 若 lim (e ) (e ) 0 j j - = → W W N N 则 X X    2 x[k] k 若 lim (e ) (e ) d 0 2 j j - = → - W W W p p N N 则 X X

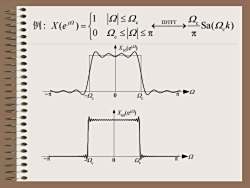
[2|≤20IDTFTSa(例：1-2.≤2|≤元元0元0

     p  = W W W W W c c 0 1 ： ( ) j 例 X e Sa( ) c IDTFT c W k W p ⎯⎯→ X10(ejW ) -p p W Wc -Wc  X60(ejW ) -p p W Wc -Wc 

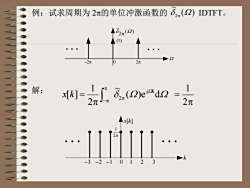
例：试求周期为2元的单位冲激函数的S（2）IDTFT。8(1)-2元2元0解：-(2)ej5kkd2K2元2元-元x[k]2013-2-1-3

例：试求周期为 2p的单位冲激函数的 ( ) IDTFT。 ~  2p W -p 0 p W  ( ) 2 ~  Wp  W W W ( )e d ~ 2 1 [ ] j 2 k x k p p p -p = p = 2 1 x[k] k -2 -1 0 1 2 2p 1 -3 3 解：

DTFT性质lejo(2) = Xr(ej°)+ jX,(ej°)X(ej?)=(ejs

DTFT性质 ( ) ( ) ( ) ( ) W W (W) W jW I j R j j j X e = X e e = X e + j X e

1. DTFT(x*[k]}= X *(e-j?)证: DTFT(x*[k]]Z三3x[k]ek当 x[]是实序列时：X(61)=*(6-1)Xr(ej°)=Xr(e-j°)X,(ej°)=-X(e-j?)

1. DTFT{ *[ ]} *( ) jW x k X e - = 证：DTFT{x *[k]}        =  j k k x k e W [ ] *( ) jW X e - = 当 x[k]是实序列时: ( ) *( ) jW jW X e X e - = ( ) ( ) W jW R j R X e X e - = ( ) ( ) W jW I j I X e X e - = -

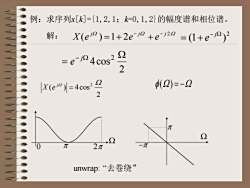
例：求序列x[k]={1,2,1；k=0,1,2] 的幅度谱和相位谱解：X(ej°)=1+2e-j +e-j2° =(l+e-j°)2.2Q= e-j? 4cos2(2)=-QX(e°) = 4cos? 2Q5一元元02元unwrap:“去卷绕

2 (1 ) - W = + j e 2 ( ) 4cos W 2 W = j X e (W) = -W unwrap: “去卷绕” 2 4cos2 W = - jW e 例：求序列x[k]={1,2,1；k=0,1,2}的幅度谱和相位谱。 0 p p W p -p W W W 2W ( ) 1 2 j j j X e e e - - 解： = + +

2. DTFT(x*[-k]}= X *(ej?)x[]实偶对称:X(ej°)= X*(ej?)X(ej°)是实偶的x[K]实奇对称：X(ej?)=-X*(ej?)X(e j2)是虚的,虚部是奇函数

2. DTFT{ *[ ]} *( ) jW x -k = X e x [k]实偶对称: ( ) *( ) jW jW X e = X e X(e jW )是实偶的 x [k]实奇对称： ( ) *( ) jW jW X e = -X e X(e jW)是虚的, 虚部是奇函数