《数字信号处理》课程教学资源（习题解答）ch7 数字滤波器的结构

7.6习题7-1.已知某数字系统的系统函数为23H(-)=(z-0.4)(-2-0.6z+0.25)试分别画出直接型、级联型、并联型结构框图。解：将H(-)表示为1H(=)=1 =~l + 0.49≥2 0.1=-3由此可画出系统的直接型结构框图，如下图(a)所示。由于系统有一单实数极点和一对共轭复数极点，故将H=)表示实系数一阶、二阶子系统的乘积，即11H(=)=1 0.4" 1 0.62l + 0.252~2由此可画出系统的级联型结构框图，如下图(b)所示。故将H(=)表示实系数一阶、二阶子系统之和0.0588 +0.5882z-10.9412H(=)=10.62-" +0.25--210.4z-l由此可画出系统的并联型结构框图，如下图(c)所示。x[K]-1x[k]y[k]0.490.60.0.10.25(a)直接型结构(b）级联型结构

7.6 习题 7-1. 已知某数字系统的系统函数为 ( 0.4)( 0.6 0.25) ( ) 2 3 − − + = z z z z H z 试分别画出直接型、级联型、并联型结构框图。 解： 将 H(z)表示为 1 2 3 1 0.49 0.1 1 ( ) − − − − + − = z z z H z 由此可画出系统的直接型结构框图，如下图(a)所示。由于系统有一单实数极点和一对共轭 复数极点，故将 H(z)表示实系数一阶、二阶子系统的乘积，即 1 1 2 1 0.6 0.25 1 1 0.4 1 ( ) − − − − − + = z z z H z 由此可画出系统的级联型结构框图，如下图(b)所示。故将 H(z)表示实系数一阶、二阶子系 统之和 1 2 1 1 1 0.6 0.25 0.0588 0.5882 1 0.4 0.9412 ( ) − − − − − + + + − = z z z z H z 由此可画出系统的并联型结构框图，如下图(c)所示。 x[k] y[k] 0.1 z −1 z −1 z −1 −0.49 x[k] y[k] z −1 z −1 −0.25 0.6 z −1 0.4 (a) 直接型结构 (b) 级联型结构

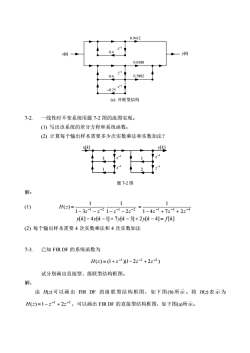
0.94121x[]0.05880.58820.60.25(c）并联型结构7-2.一线性时不变系统用题7-2图的流图实现。（1）写出该系统的差分方程和系统函数；(2）计算每个输出样本需要多少次实数乘法和实数加法？K]JA]题7-2图解：111(1)H(=):1 3-- - 2-2 1- --1 - 2--21 4=-l + 7=-3 + 2=-4[k]-4y[k-]]+7y[k-3]+2[k-4]= f[k](2）每个输出样本需要4次实数乘法和4次实数加法7-3.已知FIRDF的系统函数为H(=) = (1+ =-l )(1 2=-l + 22-2 )试分别画出直接型、级联型结构框图。解：由H()可以画出FIRDF的级联型结构框图，如下图(b)所示。将H(a)表示为H(=)=1-2-+2=-3，可以画出FIRDF的直接型结构框图，如下图(a)所示

x[k] y[k] z −1 z −1 −0.25 0.6 z −1 0.4 0.9412 0.0588 0.5882 (c) 并联型结构 7-2. 一线性时不变系统用题 7-2 图的流图实现。 (1) 写出该系统的差分方程和系统函数； (2) 计算每个输出样本需要多少次实数乘法和实数加法？ 2 3 1 −1 z x[k] y[k] −1 z −1 z −1 z 1 题 7-2 图 解： (1) 1 2 1 2 1 2 1 1 3 1 ( ) − − − − − − − − = z z z z H z 1 3 4 1 4 7 2 1 − − − − + + = z z z y[k] − 4y[k −1] + 7y[k − 3] + 2y[k − 4] = f[k] (2) 每个输出样本需要 4 次实数乘法和 4 次实数加法 7-3. 已知 FIR DF 的系统函数为 ( ) (1 )(1 2 2 ) −1 −1 −2 H z = + z − z + z 试分别画出直接型、级联型结构框图。 解： 由 H(z) 可以画出 FIR DF 的级联型结构框图，如下图(b) 所示。将 H(z) 表示为 1 3 ( ) 1 2 − − H z = − z + z ，可以画出 FIR DF 的直接型结构框图，如下图(a)所示

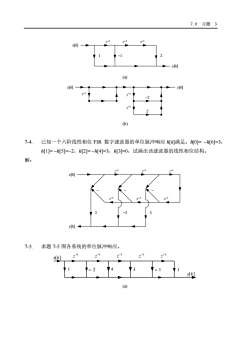
7.6习题32x[K](a)[]x[K]-2(b)7-4.已知一个六阶线性相位FIR数字滤波器的单位脉冲响应h[k]满足：h[0]=-h[6]=3h[1]=-h[5]=-2，h[2]=-h[4]=3，h[3]=0，试画出该滤波器的线性相位结构。解：x[]7-5.求题7-5图各系统的单位脉冲响应。~x[]K(a)

7.6 习题 3 −1 z −1 z −1 z −1 1 2 y[k] x[k] (a) x[k] y[k] z −1 −2 z −1 z −1 2 (b) 7-4. 已知一个六阶线性相位 FIR 数字滤波器的单位脉冲响应 h[k]满足：h[0]= −h[6]=3， h[1]= −h[5]=−2，h[2]= −h[4]=3，h[3]=0，试画出该滤波器的线性相位结构。 解： y[k] x[k] − z −1 z −1 z −1 z −1 z −1 −2 − − z −1   7-5. 求题 7-5 图各系统的单位脉冲响应。 −1 z −1 z −1 z − 2 3 y[k] x[k] 1 4 −1 z −1 z − 1 1 (a)

x[k][k](b)题7-5图解：(a)[k]=[k]-2[k-1]+ 4[k-2]+ 3[k -3]-[k- 4]+[k-5](b) h[k]=2[k]+ 3[k-1]+o[k-2]-o[k-3]-[k- 4]+[k-5]+3[k-6]+20[k -7]7-6.对于频率取样型FIR数字滤波器，为了保证系统的稳定性，通常在r圆上取样（2|H[m]Hm(=)N-1-rzm=l其中2mcos(o[m))-r=-lcos(o[m)-NHm(α)=2元m2-~212rz-lcos+N

−1 z −1 z −1 z −1 z −1 z −1 z −1 z x[k] y[k] 2 3 1 − 1 (b) 题 7-5 图 解： (a) h[k] =[k] − 2[k −1] + 4[k − 2] + 3[k − 3] −[k − 4] + [k − 5] (b) h[k] = 2[k] + 3[k −1] + [k − 2] −[k − 3] −[k − 4] + [k − 5] + 3[k − 6] + 2[k − 7] 7-6. 对于频率取样型 FIR 数字滤波器，为了保证系统的稳定性，通常在 r 圆上取样(r<1 但近似等于 1)，请修正式(7-17)、式(7-18)和式(7-19)，并画出相应的流图。 解：         + + + − − =  − = − − − 2 1 1 1 1 2 [ ] ( ) 1 [ / 2] 1 1 [0] ( ) N m m N N H m H z rz H N rz H N r z H z ， N 为奇数         + − − =  − = − − ( 1) 2 1 1 2 [ ] ( ) 1 1 [0] ( ) N m m N N H m H z rz H N r z H z ， N 为偶数 其中 1 2 2 1 ) 2 1 2 cos( ) 2 cos( [ ]) cos( [ ] ( ) − − − − + − − = r z N m rz N m m rz m Hm z    

7.6习题5H[O]1/Ny[k]x[k]H()2H[1]H,(2)2H[2]H n-(2) :2H(a)N为偶数时修正的频率取样型结构图cos([m)2元m-I2rcos(2元mrcos(o[m]L(b）实系数二阶子系统Hm(=)的结构图7-7.已知FIR数字滤波器频率特性的16个取样值为H[0]=12,H[I]=-3-i, H[2]=1+ jH[3] ~ H[13] = 0, H[14] = 1 - j, H[15] = 3 + 3j若设r=1，试计算H(=)并画出实系数形式的型结构。解：由式(7-16)，可得1- 2~16121-j-3+ i-3-j1+jH(=)1Wiel4,-I161Wit'--11-W2-11Wi6152[1-2--15= W-(16-1)W-14=W-(16-2)=W，将上式化为实系数表示式=Wl利用W1616h7172元2元4元471~16+[6cos()+2sin(2-[2cos(1- 2-161216166H(2)162元、4元-1-2cos(1-2cos1616由此可画出实系数频率取样型结构，如下图所示

7.6 习题 5 ] 2 1 2 [ N − ( ) H 2 1 H z N− x[k] y[k] 1/N z −1 −r N z −N r 2H[1] 2H[2] H1 (z) H2 (z) H[0] (a) N 为偶数时修正的频率取样型结构图 2 − r ) 2π cos( [ ] N m − r  m − cos([m]) ) 2π 2 cos( N m r z −1 z −1 (b) 实系数二阶子系统 Hm(z) 的结构图 7-7. 已知 FIR 数字滤波器频率特性的 16 个取样值为 [3] ~ [13] 0, [14] 1 j, [15] 3 3j [0] 12, [1] 3 j, [2] 1 j, = = − = − + = = − − = + H H H H H H H 若设 r=1，试计算 H(z)并画出实系数形式的型结构。 解： 由式(7-16)，可得         − − + + − − + − + + − − − + − − = − − − − − − − − − − 1 5 1 1 6 1 4 1 1 6 2 1 1 6 1 1 1 6 1 1 6 1 3 j 1 1 j 1 1 j 1 3 j 1 12 16 1 ( ) z W z W z W z W z z H z 利用 1 16 (16 1) 16 15 W16 =W =W − − − ， 2 16 (16 2) 16 14 W16 =W =W − − − ，将上式化为实系数表示式               − + − + + − + − + + + − − = − − − − − − − − 1 2 1 1 2 1 1 1 6 ) 16 4π 1 2cos( )] 16 4π ) 2sin( 16 4π 2 [2cos( ) 16 2π 1 2cos( )] 16 2π ) 2sin( 16 2π 6 [6cos( 1 12 16 1 ( ) z z z z z z z z H z 由此可画出实系数频率取样型结构，如下图所示

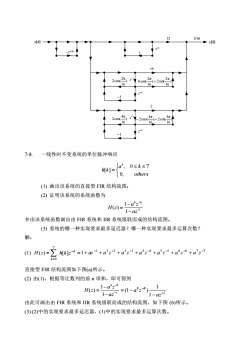
121/16[K]x[k]2元2 cos(Cn16--124元4元2cos(-2cos(_2sint1616167-8.一线性时不变系统的单位脉冲响应ak0≤k≤7h[k]=10,others(I）画出该系统的直接型FIR结构流图：(2）证明该系统的系统函数为1-a_-8H(2)=1-az-l并由该系统函数画出由FIR系统和IIR系统级联而成的结构流图。（3）系统的哪一种实现要求最多延迟器？哪一种实现要求最多运算次数？解：(1) H(2)=Z h[k]--k =1+a--l +a?2-2 +a'+a-4 +'-5 +a°,+a',-7k=0直接型FIR结构流图如下图（a)所示。(2)由(1)，根据等比数列的前n项和，即可得到1-a"--8H(=)=(1-a81αz-l由此可画出由FIR系统和IIR系统级联而成的结构流图，如下图（b)所示。(3)(2)中的实现要求最多延迟器，(1)中的实现要求最多运算次数

) 16 2π ) 2sin( 16 2π ) 6cos( + 16 2π 2cos( x[k] y[k] 1/16 1 −6 −1 −z −16 z −1 12 z −1 z −1 ) 16 4π ) 2sin( 16 4π ) − 2cos( − 16 4π 2cos(  −1 z −1 z −1 7-8. 一线性时不变系统的单位脉冲响应      = others a k h k k 0, , 0 7 [ ] (1) 画出该系统的直接型 FIR 结构流图； (2) 证明该系统的系统函数为 1 8 8 1 1 ( ) − − − − = az a z H z 并由该系统函数画出由 FIR 系统和 IIR 系统级联而成的结构流图。 (3) 系统的哪一种实现要求最多延迟器？哪一种实现要求最多运算次数？ 解： (1) k k H z h k z − = ( ) = [ ] 7 0 1 2 2 3 3 4 4 5 5 6 6 7 7 1 − − − − − − − = + az + a z + a z + a z + a z + a z + a z 直接型 FIR 结构流图如下图(a)所示。 (2) 由(1)，根据等比数列的前 n 项和，即可得到 1 8 8 1 1 ( ) − − − − = az a z H z 1 8 8 1 1 (1 ) − − − = − az a z 由此可画出由 FIR 系统和 IIR 系统级联而成的结构流图，如下图 (b)所示。 (3) (2)中的实现要求最多延迟器，(1)中的实现要求最多运算次数

7.6习题二W-l司-1一x[k]aaadsa[K](a)x[k]y[k(b)7-9.分别画出题7-1和7-3所述系统的格型结构框图。解：(1)题7-1的H(=)可以表示为1H(z) =1 =l + 0.49=-20.12-3由此可以得到as(1)=-1，as(2)=0.49，as(3)=-0.1，利用式(7-26)，有K3=α3(3)=-0.1利用式(7-28)，可得K, =4,(2) =(2) Kg: 0.39391- K3根据式(7-27)，可求出a2(I)= s()-Kga;(2),0.96061-K3再由式(7-28)，即得K, =4()=()-Kg)--0.68911-K2由确定的反射系数K1,K2,K3可得题7-1所示系统的格型结构，如图(α)所示。(2)题 7-1的H(=)可以表示为H(=)=1--l +22-3，由此可以得到 as(1)=-1,as(2)=0,a3(3)=2，与(1)相似，利用式(7-26)至式(7-28)可计算出反射系数Ki,K2,K3分别为Ki=1.0000,K2=-0.6667,K;=2.0000其格型结构如图(b)）所示

7.6 习题 7 z −1 z −1 z −1 1 y[k] x[k] a  a a  a  a  a  a  z −1 z −1 z −1 z −1 (a) x[k] y[k] z −1 z −8 −a  a (b) 7-9. 分别画出题 7-1 和 7-3 所述系统的格型结构框图。 解： (1) 题 7-1 的 H(z)可以表示为 1 2 3 1 0.49 0.1 1 ( ) − − − − + − = z z z H z 由此可以得到 a3(1)=−1, a3(2)= a3(3)=−，利用式(−)，有 K3= a3(3)=− 利用式(7-28)，可得 2 3 3 3 3 2 2 1 (2) (1) (2) K a K a K a − − = = =0.3939 根据式(7-27)，可求出 2 3 3 3 3 2 1 (1) (2) (1) K a K a a − − = =−0.9606 再由式(7-28)，即得 2 2 2 2 2 1 1 1 (1) (1) (1) K a K a K a − − = = = −0.6891 由确定的反射系数 K1,K2,K3 可得题 7-1 所示系统的格型结构，如图(a)所示。 (2) 题 7-1 的 H(z)可以表示为 1 3 ( ) 1 2 − − H z = − z + z ，由此可以得到 a3(1)=−1, a3(2)=  a3(3)=，与()相似，利用式(−)至式(−)可计算出反射系数 K1,K2,K3 分别为 K1=1.0000, K2=−0.6667, K3=2.0000 其格型结构如图(b)所示

x[]]0.1-0.39390.6890.39390.689-(a)题7-1系统的格型结构>[K][]0.66670.6667(b）题7-3系统的格型结构7-10.已知输入信号x[K]乘比例因子A以后的方差A，=16，试求使SNR≥60dB时的字长b的位数。解：由式(7-55)SNR=6.02b+10.79+10log10(α2)db≥60可以解出字长b≥87-11.已知某数字系统的系统函数为0.1=-10.1=~1H(=)=11.7-- + 0.745=-2 [1 (0.85 + j0.15)=-" [1 (0.85 j0.15)--"]（1）确定保持稳定的最小字长；(2）若使极点位置在0.5%以内变化，系数a2(=0.745)变化的百分数是多少？并确定a2在这个变化范围内时所需要的最小字长。(3）若采用8位字长的寄存器存储系数，写出该系统实际的系统函数H(=)。解：(1)4a=11.7+0.745=0.045已知最大系数max（ak）=1.7，由式(7-61)得

x[k] y[k] − −0.6891  0.6891 0.3939 −0.3939 z −1 z −1 z −1 (a) 题 7-1 系统的格型结构 x[k] y[k]     −0.6667 −0.6667 z −1 z −1 z −1 (b) 题 7-3 系统的格型结构 7-10. 已知输入信号 x[k]乘比例因子 A 以后的方差 16 2 2 A  f = ，试求使 SNR60dB 时的字 长 b 的位数。 解： 由式(7-55) 6.02 10.79 10log ( ) 60 2 SNR  b + + 10  x db  可以解出字长 b8 7-11. 已知某数字系统的系统函数为 [1 (0.85 j0.15) ][1 (0.85 j0.15) ] 0.1 1 1.7 0.745 0.1 ( ) 1 1 1 1 2 1 − − − − − − − + − − = − + = z z z z z z H z (1) 确定保持稳定的最小字长； (2) 若使极点位置在 0.5%以内变化，系数 a2(=0.745)变化的百分数是多少？并确定 a2 在这个变化范围内时所需要的最小字长。 (3) 若采用 8 位字长的寄存器存储系数，写出该系统实际的系统函数 ( ) ˆ H z 。 解： (1) ak =1−1.7 + 0.745 = 0.045 已知最大系数 max{ak} =1.7，由式(7-61)得

7.6习题90.045=0.02647≤2-(b+1)1.7即2b ≥18.89故字长b=5bits才能保证滤波器工作稳定。(2）系统的两个极点为pi=0.85+j0.15,p2=0.85-j0.15，故[p.|=|p2|=0.86310. 12-10. 12-1系统函数可表示为H(=)=1(pi + p2)2 + prP2=-2 " 1+ a,≥ + a2=-2其中a,=-(p + P2)=-1.7αz=piP2=0.745由式(7-64)可以求出极点p1,p2对系数a2变化的灵敏度为111ap21opi0.3j'aa2aazP2-PrP-P20.3j10api[op23aa2aa2可见，P2对系数a2变化的灵敏度相同，因此只研究系数a2变化对pi的影响即可。由式(7-63)可得极点pi的位置误差4p/与系数a2的误差Aa|的关系为opi[4p: ] Aa2aa2若极点位置在0.5%以内变化，即4pl//pi=0.5%，则系数a2(=0.745)变化的百分数为[Aa2[4p,// pi0.5%=0.15%10/3Jop,/aa2a2若系数α2在0.15%范围内变化，则所需要的字长b应满足[Aa2|=0.15% *a, =0.0011175>2-(b+1)由此可求出最小字长b=9。（3）若采用8位字长的寄存器存储系数，第一位用来存放整数，后七位用来存放小数，则有Q((0.1)10)=Q(0.0001100011...)=0.0001100-(0.0938)10

7.6 习题 9 ( 1) 0.02647 2 1.7 0.045 − + =  b 即 2 18.89 b 故字长 b=5bits 才能保证滤波器工作稳定。 (2) 系统的两个极点为 p1=0.85+j0.15,p2=0.85−j0.15，故 p1 = p2 = 0.8631 系统函数可表示为 2 2 1 1 1 2 1 2 1 1 2 1 1 0.1 1 ( ) 0.1 ( ) − − − − − − + + = − + + = a z a z z p p z p p z z H z 其中 a1 = −( p1 + p2 ) = −1.7 a2 = p1 p2 = 0.745 由式(7-64)可以求出极点 p1,p2 对系数 a2 变化的灵敏度为 0.3j 1 1 2 2 1 1 = − − =   a p p p , 0.3j 1 1 2 1 2 2 = − =   a p p p 3 10 2 2 2 1 =   =   a p a p 可见，,p2 对系数 a2 变化的灵敏度相同，因此只研究系数 a2 变化对 p1 的影响即可。由式(7-63) 可得极点 p1 的位置误差 p1 与系数 a2 的误差 a2 的关系为 2 2 1 1 a a p p     = 若极点位置在 0.5%以内变化，即 p1 / p1 = 0.5% ，则系数 a2(=0.745)变化的百分数为 0.15% 10 / 3 / 0.5% 1 2 1 1 2 2 = =   = p a p p a a  若系数 a2 在 0.15%范围内变化，则所需要的字长 b 应满足 2 15%* 2 a = 0. a =0.0011175>2−(b+1) 由此可求出最小字长 b=9。 (3) 若采用 8 位字长的寄存器存储系数，第一位用来存放整数，后七位用来存放小数，则有 Q{(0.1)10}=Q{0.0001100011}=0.0001100=(0.0938)10

Q((1.7)to)=Q(1.1011001100...)=1.1011010=(1.7031)0Q(0.745)10)=Q(0.1011111010...)=0.1011111=(0.7422)100.0938l故()17031-+0.7422-7-12.已知某二阶数字系统的差分方程为[k]-J[k-1]+0.75y[k-2]=x[k]若采用字长b=3(不含符号位)的定点运算，舍入处理，试求当x[k]=0,[-2]=0,[-1]=0.5时的输出[k]（取前9点值)。解：若对乘法运算采用舍入量化处理，相应的差分方程为[k]=x[k]+[k-1]-Q(0.75[k-2]]将十进制数用字长b=3的二进制数表示，有(0.75)10=0.110，[-1)=(0.5)10=0.100，则滤波器的输出[k]为[0]=x[0] +Q([-1])-Q(0.110[-2])=0.100=(0.5)10[1]=x[1]+Q([0])-Q(0.110[-1])=0.100-0.011=0.001=(0.125)10[2]=x[2]+Q([1])-Q(0.110[0])=0.001-0.011=1.010-(-0.25)10[3]=x[3]+Q([2]) -Q(0.110[1]) =1.010-0.001=1.011=(-0. 375)10[4]=x[4]+Q([3])-Q(0.110[2])=1.011+0.010=1.001=(-0. 125)10[5]=x[5]+Q([4])-Q(0.110[3])=1.001+0.010=0.001=(0. 125)10[6]=x[6]+Q([5])-Q(0.110[4])=0.001+0.001=0.010=(0.25)10[7]=x[7]+Q([6]}-Q(0.110[5])=0.010-0.001=0.001=(0.125)10[8]=x[8] +Q([7]) -Q(0.110[6]) =0.001-0.010=1.001=(-0, 125)10

Q{(1.7)10}=Q{1.1011001100}=1.1011010=(1.7031)10 Q{(0.745)10}=Q{0.1011111010}=0.1011111=(0.7422)10 故 1 2 1 1 1.7031 0.7422 0.0938 ( ) ˆ − − − − + = z z z H z 7-12. 已知某二阶数字系统的差分方程为 y[k]− y[k −1]+ 0.75y[k − 2] = x[k] 若采用字长 b=3(不含符号位)的定点运算，舍入处理，试求当 x[k] = 0, y ˆ[−2] = 0, y ˆ[−1] = 0.5 时的输出 y ˆ[k] （取前 9 点值）。 解： 若对乘法运算采用舍入量化处理，相应的差分方程为 y ˆ[k] = x[k] + y ˆ[k −1] − Q{0.75y ˆ[k − 2]} 将十进制数用字长 b=3 的二进制数表示，有(0.75)10=0.110，y ˆ[−1] = (0.5)10 = 0.100 ，则滤波 器的输出 y ˆ[k] 为 y ˆ[0] = x[0] + Q{y ˆ[−1]}− Q{0.110 y ˆ[−2]} =0.100=(0.5)10 y ˆ[1] = x[1] + Q{y ˆ[0]}− Q{0.110 y ˆ[−1]} =0.100−0.011=0.001=(0.125)10 y ˆ[2] = x[2] + Q{y ˆ[1]}− Q{0.110 y ˆ[0]} =0.001− 0.011=1.010=(−0. 25)10 y ˆ[3] = x[3] + Q{y ˆ[2]}− Q{0.110 y ˆ[1]} =1.010− 0.001=1.011=(−0. 375)10 y ˆ[4] = x[4] + Q{y ˆ[3]}− Q{0.110 y ˆ[2]} =1.011+ 0.010=1.001=(−0. 125)10 y ˆ[5] = x[5] + Q{y ˆ[4]}− Q{0.110 y ˆ[3]} =1.001+ 0.010=0.001=(0. 125)10 y ˆ[6] = x[6] + Q{y ˆ[5]}− Q{0.110 y ˆ[4]} =0.001+ 0.001=0.010=(0. 25)10 y ˆ[7] = x[7] + Q{y ˆ[6]}− Q{0.110 y ˆ[5]} =0.010− 0.001=0.001=(0. 125)10 y ˆ[8] = x[8] + Q{y ˆ[7]}− Q{0.110 y ˆ[6]} =0.001− 0.010=1.001=(−0. 125)10