《数字信号处理》课程教学资源（教案讲义）ch7 数字系统的结构

第7章数字系统的结构■IR数字滤波器的基本结构■FIR数字滤波器的基本结构■格型结构■数字滤波器结构的MATLAB实现7.1IIR数字滤波器的基本结构■直接型结构■级联型结构■并联型结构、IIR数字滤波器的直接型结构M2b"N1Y(a)i=0Zb2H,(z)=H(2):NW(=)i=01+a,--j1+Za,--ij=1j=lW(=)H,(2)=X()w[k]=box[k]+b,x[k-1]+...+bwx[k-M]J[k]=w[k]-a,x[k-]]-a,x[k-2]-...-avx[k-N]直接I型结构设M-Nw[k]= box[k]+b,x[k-1]+...+brx[k-N]y[k]=w[k]-a,x[k-]-a,x[k-2]-...-a[k-N]w[k]y[k][K]64-αib2- a2-...2an-!bNan购

第 7 章 数字系统的结构 ◼ IIR 数字滤波器的基本结构 ◼ FIR 数字滤波器的基本结构 ◼ 格型结构 ◼ 数字滤波器结构的 MATLAB 实现 7.1 IIR 数字滤波器的基本结构 ◼ 直接型结构 ◼ 级联型结构 ◼ 并联型结构 一、IIR 数字滤波器的直接型结构   = − = − + = N j j j M i i i a z b z H z 1 0 1 ( )   = = − − + = N j j j M i i i a z b z 1 0 1 1 ( ) ( ) ( ) 2 W z Y z H z = ( ) ( ) ( ) 1 X z W z H z = [ ] [ ] [ 1] [ ] w k = b0 x k +b1 x k − ++bN x k − M [ ] [ ] [ 1] [ 2] [ ] y k = w k − a1 x k − − a2 x k − −− aN x k − N 直接 I 型结构 设 M=N [ ] [ ] [ 1] [ ] w k = b0 x k +b1 x k − ++bN x k − N [ ] [ ] [ 1] [ 2] [ ] y k = w k − a1 x k − − a2 x k − −− aN x k − N − a2 − a1 − aN −1 N − aN b  b2 b1 −1 z y[k] −1 z −1 z −1 z  b0 −1 z −1 z −1 z −1 z x[k] w[k]

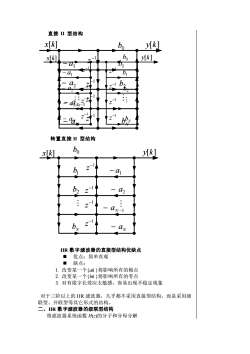
直接IⅡI型结构x[k]y[k]bobo[k]x[k]Daibiaiba2-4: :cNi-Z7bhn=a福转置直接ⅡI型结构boy[k]x[k]b,ayb2a2V-1anIIR数字滤波器的直接型结构优缺点■优点：简单直观■缺点：1.改变某一个ak！将影响所有的极点2.改变某一个(bk)将影响所有的零点3.对有限字长效应太敏感，容易出现不稳定现象对于三阶以上的IIR滤波器，几乎都不采用直接型结构，而是采用级联型、并联型等其它形式的结构。二、IIR数字滤波器的级联型结构将滤波器系统函数H(=)的分子和分母分解

直接 II 型结构 − a2 − a1 − aN −1 − aN bN b2 b1 −1 z y[k] −1 z −1 z −1 z  b0 x[k] − a2 − a1 − aN −1 − aN bNb2 b1 −1 z y[k] −1 z −1 z −1 z  b0 −1 z −1 z −1 z −1 z x[k] 转置直接 II 型结构 − a2 − a1 − aN −1 N − aN b  b2 b1 −1 z y[k] −1 z −1 z −1 z  x b0 [k] IIR 数字滤波器的直接型结构优缺点 ◼ 优点：简单直观 ◼ 缺点： 1. 改变某一个{ak }将影响所有的极点 2. 改变某一个{bk }将影响所有的零点 3. 对有限字长效应太敏感，容易出现不稳定现象 对于三阶以上的 IIR 滤波器，几乎都不采用直接型结构，而是采用级 联型、并联型等其它形式的结构。 二、IIR 数字滤波器的级联型结构 将滤波器系统函数 H(z)的分子和分母分解

为一阶和二阶实系数因子之积的形式I(1-z,2")(1+αx2- +α2,x-)H(=)=K k(1- Pe=-)(1+ βux-* + β2,±=-)=-+1+α1,--* +α2,--2H()=A=AIIHi1+ β, 2-* + β,,-2-画出各二阶基本节的直接型结构，再将它们级联。级联型结构信号流图K]x[k]_1~-βu-βuauau+2-1β2-B,α21d基于直接II型的级联型结构x[k]-y[k]"-BL-"- βauA- βa-- βalaza2t基于转置直接II型的级联型结构IIR数字滤波器的级联型结构优点优点：1.硬件实现时，可以用一个二阶节进行时分复用2.每一个基本节系数变化只影响该子系统的零极点3.对系数变化的敏感度小，受有限字长的影响比直接型低三、IIR数字滤波器的并联型结构将滤波器系统函数H()展开成部分分式之和，并将一阶系统仍采用二阶基本节表示IYox +Yux-H(=)= + 1 βr,x-l - β2,±=-2画出各二阶基本节的直接型结构，再将它们并联。并连型结构信号流图

为一阶和二阶实系数因子之积的形式     = − − = − = − − = − − + + − + + = 1 2 1 2 1 2 2, 1 1, 1 1 1 2 2, 1 1, 1 1 (1 ) (1 ) (1 ) (1 ) ( ) N k k k N k k M k k k M k k p z z z z z z z H z K     ( ) 1 1 ( ) 1 2 2, 1 1, 2 2, 1 1, 1 A H z z z z z H z A i L i i i i i L i = − − − − = =  + + + + =      画出各二阶基本节的直接型结构，再将它们级联。 级联型结构信号流图 基于直接 II 型的级联型结构 基于转置直接 II 型的级联型结构 IIR 数字滤波器的级联型结构优点 优点： 1. 硬件实现时，可以用一个二阶节进行时分复用 2. 每一个基本节系数变化只影响该子系统的零极点 3. 对系数变化的敏感度小，受有限字长的影响比直接型低 三、IIR 数字滤波器的并联型结构 将滤波器系统函数 H(z)展开成部分分式之和，并将一阶系统仍 采用二阶基本节表示 2 2, 1 1, 1 0, 1, 1 0 1 ( ) − − − = − − + = + z z z H z k k k k L k      画出各二阶基本节的直接型结构，再将它们并联。 并连型结构信号流图 11 − 11 −1 z y[k] −  21  21 −1 z 1L − 1L −1 z −  2L  2L −1 z A x[k] − 11 11 −1 z x[k] y[k] −  21  21 −1 z − 1L 1L −1 z −  2L  2L −1 z A

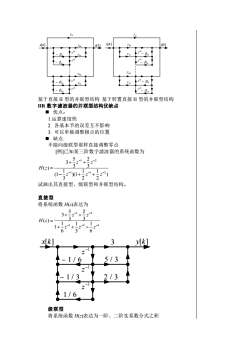
Yox[K][k][k]Y]-- β-YoLY02~--- βu-βuLYut7- βar- βz基于直接II型的并联型结构基于转置直接II型的并联型结构IIR数字滤波器的并联型结构优缺点■优点：1.运算速度快2.各基本节的误差互不影响3.可以单独调整极点的位置■缺点：不能向级联型那样直接调整零点[例]已知某三阶数字滤波器的系统函数为25.I3+-+-233H(-)=-21+(1-一+-222试画出其直接型、级联型和并联型结构。直接型将系统函数H()表达为5-13+11H(-) =1+366x[k]3y[k]Z5 / 31/ 672/3/31/6级联型将系统函数H(2)表达为一阶、二阶实系数分式之积

− 11 01  −1 z x[k] −  21 −1 z y[k] − 1L −1 z −  2L −1 z 0  11  1L  0L  − 11 01  −1 z −  21 −1 z y[k] − 1L −1 z −  2L −1 z 0  11  1L  0L  x[k] 基于直接 II 型的并联型结构 基于转置直接 II 型的并联型结构 IIR 数字滤波器的并联型结构优缺点 ◼ 优点： 1.运算速度快 2. 各基本节的误差互不影响 3. 可以单独调整极点的位置 ◼ 缺点: 不能向级联型那样直接调整零点 [例]已知某三阶数字滤波器的系统函数为 ) 2 1 2 1 )(1 3 1 (1 3 2 3 5 3 ( ) 1 1 2 1 2 − − − − − − + + + + = z z z z z H z 试画出其直接型、级联型和并联型结构。 直接型 将系统函数 H(z)表达为 1 2 3 1 2 6 1 3 1 6 1 1 3 2 3 5 3 ( ) − − − − − + + − + + = z z z z z H z 级联型 将系统函数 H(z)表达为一阶、二阶实系数分式之积 − 1 / 3 − 1 / 6 1 / 6 2 / 3 5 / 3 −1 z x[k] y[k] −1 z −1 z 3

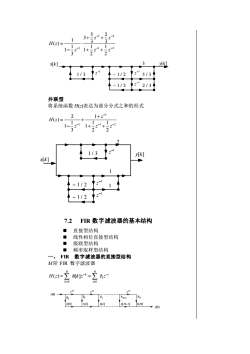
3--3H(-):1-21-1+322y[k]x[k]4-4-1/25/31/32/3-1/2并联型将系统函数H(-)表达为部分分式之和的形式1+ 2~l2H(z)=+11-51/3[k]x[k]1/21/27.2FIR数字滤波器的基本结构直接型结构线性相位直接型结构限级联型结构圆频率取样型结构数字滤波器的直接型结构FIRM阶FIR数字滤波器MMh[k]-k =]H(a)=2Z b,2-ik=0i=0-x[1] -bbbay-1h[0]h[1] [2][M-1][M][]

1 2 1 2 1 2 1 2 1 1 3 2 3 5 3 3 1 1 1 ( ) − − − − − + + + +  − = z z z z z H z 并联型 将系统函数 H(z)表达为部分分式之和的形式 1 2 1 1 2 1 2 1 1 1 3 1 1 2 ( ) − − − − + + + + − = z z z z H z 7.2 FIR 数字滤波器的基本结构 ◼ 直接型结构 ◼ 线性相位直接型结构 ◼ 级联型结构 ◼ 频率取样型结构 一、 FIR 数字滤波器的直接型结构 M 阶 FIR 数字滤波器 i i M i k M k H z h k z b z − = − = =  =  0 0 ( ) [ ] −1 z −1 z −1 z b0 b1 b2 bM −1 bM x[k] y[k] h[0] h[1] h[2] h[M−1] h[M] 1 / 3 −1 z − 1 / 2 −1 z −1 z 1 − 1 / 2 1 x[k] y[k] 2 1 / 3 −1 z x[k] y[k] − 1 / 2 −1 z −1 z 3 5 / 3 − 1 / 2 2 / 3

M+1个乘法器，M个延迟器，M个加法器二、线性相位FIRDF结构利用h[k]的对称特性：h[k]=土h[M-k]M为偶数-1_MM,Hk(=*±=~(M-k).H(=)= 12+h2k=0x[]Mh[1]-1h[0]h[2]h-y[k]相同系数的共用乘法器，只需M/2+1个乘法器M为奇数M-12(M-kh[k](2-* ± 2-(H()=k=0x[K]h[0]h[2]h[1][] 4相同系数的共用乘法器，只需(M+1)2个乘法器三、FIR数字滤波器的级联型结构将H(=)分解为若干个实系数一阶二阶因子相乘b[0]x[A][]1-BuBB21BBzt2L=M个延迟器，2L+1=M+1个乘法器，2L=M个加法器特点：可以分别控制每个子系统的零点

M+1 个乘法器，M 个延迟器，M 个加法器 二、线性相位 FIR DF 结构 利用 h[k]的对称特性： h[k]= ±h[M-k] M 为偶数 2 1 2 0 ( ) ] 2 ( ) [ ]( ) [ M M k k M k z M H z h k z z h − − = − − − =   + 相同系数的共用乘法器，只需 M/2+1 个乘法器 M 为奇数 ( ) [ ]( ) 2 1 0 ( )  − = − − − =  M k k M k H z h k z z 相同系数的共用乘法器，只需(M+1) /2 个乘法器 三、 FIR 数字滤波器的级联型结构 将 H(z)分解为若干个实系数一阶二阶因子相乘 2L=M 个延迟器，2L+1=M+1 个乘法器，2L=M 个加法器 特点：可以分别控制每个子系统的零点 11  21 1L  2L 12  22 x[k] y[k] −1 z −1 z h[0]−1 z −1 z −1 z −1 z −1 z ] 2 3 [ M − h ] 2 1 [ M − h 1 x[k] y[k] h[0] h[1] h[2] 1 1 1 1 −1 z −1 z −1 z −1 z −1 z −1 z 1] 2 [ − M h ] 2 [ M h x[k] y[k] h[0] h[1] h[2] 1 1 1 1 −1 z −1 z −1 z −1 z −1 z −1 z

四、 FIR数字滤波器的频率取样型结构-H[m]1- 2~H(z):01-W~"2-INH[0]1/Nx[K]y[k]weHWN!H[N-1]W(N-I) 频率取样型结构分析1-2"N H[m]H(z)=N1-W"-FIR子系统一梳状滤波器一阶IIR子系统z= k/N,=0,1,.,N-1 =eik/N,k=0,,.,N-1零点与IIR子系统极点相消，使系统具有FIR特性频率取样型结构分析存在问题：在有限字长情况下，系数量化后极点不能和零点抵消，使FIR系统不稳定。解决方法：在r圆上进行(r<1但近似等于1)取样，即用rz-1代替z-1,使极点和相应的零点移到单位圆内。1-rNz-N N-.H[m]H(-)~1-rW-"--N实系数频率取样型结构一阶利用H[m]和旋转因子的对称性，将二个复系数IIR子系统合并成一个实系数二阶子系统。N为奇数N/2-1-2-N[H[0] H[N/2]Z2|H[m]|H.(2)H(2)=N1-2-1+z-m=l

四、 FIR 数字滤波器的频率取样型结构  − = − − − − − = 1 0 1 1 1 [ ] ( ) N m m N N W z H m N z H z 频率取样型结构分析  − = − − − − − = 1 0 1 1 1 [ ] ( ) N m m N N W z H m N z H z FIR 子系统—梳状滤波器 一阶 IIR 子系统 , 0,1, , 1 j2π / z = e k = N − k N k  , 0,1, , 1 j2π / p = e k = N − k N k  零点与 IIR 子系统极点相消，使系统具有 FIR 特性 频率取样型结构分析 存在问题： 在有限字长情况下，系数量化后极点不能和零点抵消，使 FIR 系统不稳定。 解决方法： 在 r 圆上进行(r<1 但近似等于 1)取样，即用 rz-1 代替 z-1， 使极点和相应的零点移到单位圆内。  − = − − − − −  1 0 1 1 1 [ ] ( ) N m m N N N rW z H m N r z H z 实系数频率取样型结构 利用 H[m]和旋转因子的对称性，将二个复系数 IIR 一阶 子系统合并成一个实系数二阶子系统。 N 为奇数       + + + − − =  − = − − − 2 1 1 1 1 2 [ ] ( ) 1 [ / 2] 1 1 [0] ( ) N m m N H m H z z H N z H N z H z 0 WN −1 WN −(N−1) WN x[k] y[k] −1 z −1 z −1 z H[0] H[1] H[N−1] 1/N N z − −

N为偶数(N-1)/2H[O]1-z'H(2) =2HmH.(N1-2-m=l其中2元mcos(0[m])-2-′ cos(g[m]-3NHm()=2m)+r22-21-22" cos(N例：设计一M阶实系数FIR，已知H[O]-1，H[1]=1，画出其频率取样型结构。解：频率抽样点数N=M+11-2-(N+)H(2)=-W-(N-IN+11- 2-l1-W-由 H[N-1]- H[1]-1, 和 W-(N-1) =W)2-2cos(1-2 (N+1)V+H(2)N+12元1-1-2cos(N+1实系数频率取样型结构流图I/N[K]x[K]2元2cos(T-21-2cos(N7.3格型结构■全零点(AZ)滤波器的格型结构■全极点（AP）滤波器的格型结构■有极点和零点滤波器的格型结构三种滤波器的系统函数全零点(AZ)滤波器a,(n)="nA(z)=1+ n=l

N 为偶数       + − − =  − = − − ( 1) 2 1 1 2 [ ] ( ) 1 1 [0] ( ) N m m N H m H z z H N z H z 其中 1 2 2 1 ) 2 1 2 cos( ) 2 cos( [ ]) cos( [ ] ( ) − − − − + − − = r z N m z N m m z m H z m     例：设计一 M 阶实系数 FIR，已知 H[0]=1，H[1]=1，画出其 频率取样型结构。 解：频率抽样点数 N=M+1       − + − + + − − = − − − + − − + − − + ( 1) 1 1 1 1 1 1 ( 1) 1 1 1 1 1 1 1 1 ( ) N z W z W z z H z N N N N 由 H[N-1]= H[1]=1，和 ( 1) 1 N N WN = W − −           + + − + − + + − − = − − − − − + 1 2 1 1 ( 1) ) 1 2 1 2cos( ) 1 2 2 2cos( 1 1 1 1 ( ) z z N z N N z z H z N   实系数频率取样型结构流图 7.3 格型结构 ◼ 全零点(AZ)滤波器的格型结构 ◼ 全极点（AP）滤波器的格型结构 ◼ 有极点和零点滤波器的格型结构 三种滤波器的系统函数 全零点(AZ)滤波器 n p p n A z a n z − = ( ) =1+ ( ) 1 ) 2 2cos( N  − ) 2 2 cos( N  x[k] y[k] 1/N N z − − z−1 z−1 z−1 1 1 −1

全极点(AP)滤波器1H(=)=A()1+5Za.(n)-"nhaAZAP滤波器PWbm2B(=)M=0H(z)=A(z)A(=)、全零点(AZ)滤波器的格型结构e,[k]e [k]e([k]eflk][K]Mk]AKK.y'[K]e,[k]e;[k]e,[k]e,[k]D-l[k]eb-,[k]IkAZ系统的基本格形单元反射系数 Kp 的确定根据系统函数由高阶系数递推各低阶反射系数KpK,=a,(p)ap-1(0)=,(0)-K,a,(p-I)(i= 1,2,.-, p-1)1- K,ap-(0)=(0)-K,a,(p-I)(i=1,2,",p-1)1-K,二、全极点（AP）滤波器的格型结构x[K] =e,[K]e,-[k]ep-2[K]e[k]e[k]Mk]Ke,[k]ep-[k]e,[k]"[k]

全极点(AP)滤波器 n p p n a n z A z H z − = + = = 1 ( ) 1 ( ) 1 ( ) 1 AZAP 滤波器 ( ) ( ) ( ) ( ) 0 A z B z A z b z H z m m p m = = − =  一、全零点(AZ)滤波器的格型结构 AZ 系统的基本格形单元 反射系数 Kp 的确定 根据系统函数， 由高阶系数递推各低阶反射系数 Kp K a ( p) p = p ( 1,2, , 1) 1 ( ) ( ) ( ) 1 2 = − − − − − = i p K a i K a p i a i p p p p p  ( 1,2, , 1) 1 ( ) ( ) ( ) 1 2 = − − − − − = i p K a i K a p i a i p p p p p  二、全极点（AP）滤波器的格型结构 −1 z −1 z −1 z x[k] e [k] f = p y[k] − K1 Kp−1 − Kp−1 K1 [ ] 0 e k f [ ] 1 e k f [ ] 2 e k f p− [ ] 1 e k f p− e [k] b p [ ] 1 e k b p− [ ] 1 e k b [ ] 0 e k b − Kp Kp [ ] 1 e k f p− Kp e [k] f p [ ] 1 e k b p− e [k] b p −1 Kp z −1 z −1 z K2 −1 z K1 y[k] [ ] 0 e k f [ ] 1 e k f [ ] 2 e k f e [k] f p e [k] b p [ ] 2 e k b [ ] 1 e k b [ ] 0 e k b K1 K2 Kp Kp y [k] b x[k]

e'[k][KAP系统的基本格型单元三、有极点和零点滤波器的格型结构ef[K]e [k]x[K]=e,[K]e,-[k]e([k]第第p阶第1阶p-1附e,[k]e,[Kk]e [k]e,[k].[k]]图中的方框是如下基本格型单元e,[k][k]e'[k][k格型结构中K,C参数的确定1.K参数利用AZ系统反射系数Kp的递推公式递推出2.确定cpC,=b,3.递推求出c参数Pb.=c.+Zca,(i-m)m=0,1,2,"",p-147.4数字滤波器结构的MATLAB实现■直接型结构■级联型结构■并联型结构■格型结构一、直接型结构MATLAB描述：IIR由两个行矢量b和a描述，b包含（bn)系数，a包含(an)系数FIR由包含(bn)系数的行矢量b描述

AP 系统的基本格型单元 三、有极点和零点滤波器的格型结构 图中的方框是如下基本格型单元 格型结构中 K , C 参数的确定 1. K 参数利用 AZ 系统反射系数 Kp 的递推公式递推出 2. 确定 cp p bp c = 3. 递推求出 c 参数 ( ) 0,1,2, , 1 1 = +  − = − = + b c c ai i m m p p i m m m i  7.4 数字滤波器结构的 MATLAB 实现 ◼ 直接型结构 ◼ 级联型结构 ◼ 并联型结构 ◼ 格型结构 一、直接型结构 MATLAB 描述： IIR 由两个行矢量 b 和 a 描述，b 包含{bn}系数，a 包含{an} 系数 FIR 由包含{bn}系数的行矢量 b 描述 −1 z − Kp Kp [ ] 1 e k f p− e [k] f p [ ] 1 e k b p− e [k] b p 第p阶 第 p-1阶 第1阶 c p c p−1 c p−2 y[k] 1 c 0 c x[k] e [k] f = p [ ] 0 e k f [ ] 1 e k f [ ] 2 e k f p− [ ] 1 e k f p− e [k] b p [ ] 1 e k b p− [ ] 1 e k b [ ] 0 e k b [ ] 2 e k b p− −1 z − Kp Kp [ ] 1 e k f p− e [k] f p [ ] 1 e k b p− e [k] b p