《数字信号处理》课程教学资源（教案讲义）ch5 FIR数字滤波器的设计

第5章FIR数字滤波器的设计5. 1线性相位FIR滤波器的性质线性相位系统的时域特性线性相位系统的频域特性线性相位系统H(=)的零点分布特性FIR滤波器的定义MH(2)=Z b,=-kk0M阶（长度N=M+1）的FIR数字滤波器[bk=0,]..,Mh[k] =[o其它FIR滤波器的特点1]h[K]在有限范围内非零，系统总是稳定的。2)容易设计成线性相位3)可利用FFT实现4)运算量比IIR大FIR滤波器设计指标AHein)1+0,1-8p过渡带通带阻带Q02p2s严格线性相位定义H(eig) =|H(ein)leje()若(W)=-aW,则称系统H(2)是严格线性相位的。例：单频信号exp(jWOk)通过线性相位(LTI)系统的响应T(e i2ok ) = H(ejgo )lejpo(k-a)20le

第 5 章 FIR 数字滤波器的设计 5.1 线性相位 FIR 滤波器的性质 • 线性相位系统的时域特性 • 线性相位系统的频域特性 • 线性相位系统 H(z)的零点分布特性 FIR 滤波器的定义 k k M k H z b z − = =  0 ( ) M 阶(长度 N=M+1) 的 FIR 数字滤波器 h[k] =    = 0 其它 bk k 0,1,,M FIR 滤波器的特点 1)h[k]在有限范围内非零，系统总是稳定的。 2)容易设计成线性相位 3)可利用 FFT 实现 4)运算量比 IIR 大 FIR 滤波器设计指标 严格线性相位定义 j j j ( ) (e ) (e ) e    =  H H 若 f(W)= - aW, 则称系统 H(z)是严格线性相位的。 例： 单频信号 exp(jW0 k)通过线性相位(LTI)系统的响应 j j j ( ) 0 0 0 {e } (e ) e    − = k k T H 通带 过渡带 阻带   p  s ej   p − p s

广义线性相位定义H(ej)= A(2)e-(a+P)A(W)称为幅度频函数线性相位系统的时域特性V下定理：H(=)=b,=-*为线性相位的充要条件为 h[K]=±h[M-k]=03M=4偶对称M=3偶对称M=4奇对称M=3奇对称线性相位系统的频域特性1)1型：(h[k]-h[M-k],M为偶数)例: M=4, h[K]-[h[0], h[1], h[2], h[1], h[0]H(e/)=h[0](1+e-j4)+h[1](e-/ +e-J32)+ h[2]e-/20=2h[0]e-/2 cos22+2h[]e-/2 cos+[2]e-120A(2) = h[2]+ 2h[2 -1]cos Q2 + 2h[2 -2]cos 2QL=M/22h[L-k]cosk2=Ea[k]coskA(2)= h[]+Zk=(k=2a[k]coskA(-2)= A (2)A(Q+2元)= A(2)A(2元 -Q2)= A(2)A(W)关于0和p点偶对称A(W)关于0和p点偶对称H(ej)=e-jn4cosQ/2

广义线性相位定义 j j( ) (e ) ( )e  −  H = A  A (W)称为幅度频函数 线性相位系统的时域特性 定理： k k M k H z b z − = =  0 ( ) 为线性相位的充要条件为 h[k]=h[M-k] M=4 偶对称 M=3 偶对称 M=4 奇对称 M=3 奇对称 线性相位系统的频域特性 1) 1 型: (h[k]=h[M-k], M 为偶数) 例：M=4 , h[k]={h[0], h[1], h[2], h[1], h[0]}  −  −  −  −  =     4 3 2 ( ) [0](1 ) [1]( ) [2] j j j j j H e h e h e e h e −  −  −  =   2 2 2 2 [0] cos 2 2 [1] cos [2] j j j h e h e h e A() = h[2] 2h[2 −1]cos  2h[2 − 2]cos 2 L = M / 2  =  −  =   = = A h L h L k k a k k L k L k ( ) [ ] 2 [ ]cos [ ]cos 1 0  =   = A a k k L k ( ) [ ]cos 0 A(  2π) = A() A(−) = A () A(2 −) = A() A (W)关于 0 和 p 点偶对称 A (W)关于 0 和 p 点偶对称 (e ) e 4cos / 2 j j 2 =   −  H 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4

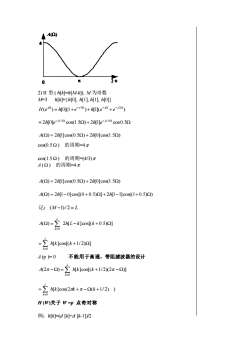
A(2)2元元02)II 型:(h[K]=h[M-k]),M 为奇数M=3 h[K]={h[0], h[1], h[1], h[0]]H(ej°)= h[0](1+e-j32)+ h[1](e-jn +e-j22)=2h[0]e-159 cos(1.52)+2h[1]e-1.50 cos0.5A(2)=2h[1]cos(0.52)+2h[0]cos(1.5)cos(0.52）的周期=4元cos(1.52）的周期=(4/3)元A（2）的周期=4元A(2)=2h[1|cos(0.52)+2h[0|cos(1.52)A() =2h[1-0]cos[(0+0.5)]+2h[1-1]cos(1+0.5))记：(M-1)/2=LA4(2)=2h[L-k]cos[(k +0.5)2]K=0b[k]cos[(k +1/2)]k=0A(p)=0不能用于高通、带阻滤波器的设计A(2元-2)=b[k]cos[(k +1/2)(2元-2)]k0Kb[k]cos(2元k+元-2(k+1/2))k=0H(W)关于W=p点奇对称例: h[K]=(d [K]+d [k-1]2

 2  4 0 A()  2  4 0 A()  2  4 0 A() 2) II 型:( h[k]=h[M-k]), M 为奇数 M=3 h[k]={h[0], h[1], h[1], h[0]} ( ) [0](1 ) [1]( )  − 3 −  − 2 =    j j j j H e h e h e e =    −  −  2 [0] cos(1.5 ) 2 [1] cos0.5 j1.5 j1.5 h e h e A() = 2h[1]cos(0.5)  2h[0]cos(1.5) cos(0.5  ) 的周期=4  cos(1.5  ) 的周期=(4/3)  A (  ) 的周期=4  A() = 2h[1]cos(0.5)  2h[0]cos(1.5) A() = 2h[1− 0]cos[(0  0.5)] 2h[1−1]cos((1 0.5)) 记：(M −1)/ 2 = L ( ) 2 [ ]cos[( 0.5) ] 0  =  −   = A h L k k L k [ ]cos[( 1/ 2) ] 0 =    = b k k L k A (p )= 0 不能用于高通、带阻滤波器的设计 (2 ) [ ]cos[( 1/ 2)(2 )] 0 − =   − = A  b k k  L k [ ]cos(2 ( 1/ 2) ) 0 =   −  = b k k k L k   H (W)关于 W =p 点奇对称 例：h[k]=(d [k]+d [k-1])/2

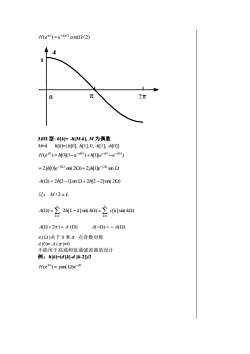
H(ejg)=e-jin/2 cos(2/2)AA1元2元03]III型：h[k]=-h[M-k],M为偶数M=4h[k]={h[0], h[1], 0, -h[1], -h[0]]H(ej9)= h[0](1-e-j4)+ h[1](e-j0 -e-j32)= 2jh[0]e-j22 sin(292) +2jh[1]e-j2° sin 2A(2) = 2h[2-1]sin 2+2h[2 -2]sin(22)记：M/2=L222A(2) = 2h[L-k]sin( k2)=c[k]sin( k)1k=1A(2+2元)= A (2)A(-2)= - A(Q2)A(Q)关于0和元点奇数对称A(0)=A(元)=0不能用于高通和低通滤波器的设计例: h[K]-(d [k]-d [k-2])/2H(ej)= jsin(2)e-jn

(e ) e cos( / 2) j j / 2 =   −  H 3)III 型: h[k]= -h[M-k], M 为偶数 M=4 h[k]={h[0], h[1], 0, -h[1], -h[0]} ( ) [0](1 e ) [1]( e )  − j4 −  − j3 = −  − j j H e h h e =    −  −  2j [0]e sin( 2 ) 2j [1]e sin j2 j2 h h A() = 2h[2 −1]sin   2h[2 − 2]sin( 2) 记： M / 2 = L ( ) 2 [ ]sin( ) [ ]sin( ) 1 1  =  −  =   = = A h L k k c k k L k L k A(  2 ) = A () A(−) = − A() A (  )关于 0 和  点奇数对称 A (0)= A (  )=0 不能用于高通和低通滤波器的设计 例：h[k]=(d [k]-d [k-2])/2  −  =  j j H(e ) jsin( )e 0 1   A ()

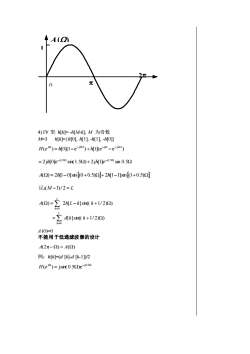
1(2)22元04)IV型:h[Kk]=-h[M-k],M为奇数M=3 h[k]=(h[0], h[1], -h[1], -h[0]]H(ej9)= h[0](1-e-j3)+h[1](e-j2 -e-j22)=2jh[0]e-j1.50 sin(1.52)+2jh[]e-i1.50 sin 0.5A(2)=2h[1-0]sin [(0+0.5)]+2h[1-1]sin[(1+0.5)2记:(M-1)/2=LA(2)=2 2h)[L-klsi(k+1/2)2)K0-2.d[k]sin(k +1/2)2)k=0A (0)=0不能用于低通滤波器的设计A(2元-2)=A(Q)例: h[K]-(d [K]-d [k-1]/2H(e/°)= jsin( 0.52)e-j0.50

4) IV 型: h[k]= -h[M-k], M 为奇数 M=3 h[k]={h[0], h[1], -h[1], -h[0]} ( ) [0](1 e ) [1](e e )  − j3 − j − j2 H e = h −  h − j =    −  −  2j [0]e sin(1.5 ) 2j [1]e sin 0.5 j1.5 j1.5 h h A() = 2h[1−0]sin(00.5)2h[1−1]sin(10.5) 记：(M −1)/ 2 = L [ ]sin(( 1/ 2) ) ( ) 2 [ ]sin(( 1/ 2) ) 0 0 =    = −     = = d k k A h L k k L k L k A (0)=0 不能用于低通滤波器的设计 A(2π −) = A() 例：h[k]=(d [k]-d [k-1])/2  −  =  j0.5 ( ) jsin( 0.5 )e j H e 0 A() 1  

P-12元元0线性相位FIR滤波器频率响应一般形式可写为H(eig)=ei-0.5M+β) A(2)表5-1四种线性相位FIR滤波器的性质1IIIIIV类型偶奇偶奇阶数M[]的对称性偶对称偶对称奇对称奇对称A()关于O-0的对称性奇对称偶对称偶对称奇对称A(2)关于0=元的对称性偶对称奇对称奇对称偶对称2元4元2元4元A(2)的周期β000.5元0.5元00A(0)任意任意A(m)00任意任意LP,HP,B LP, BP可适用的滤波器类型微分器,Hilbert微分器,HilbertP,BS等变换器，HP变换器线性相位系统H(z)的零点分布特性h[k]=±h[M -k] = H()=±z-MH(--')Z=0不可能有系统的零点.zk是系统的零点，则zk-I也是系统的零点。·:h[K]是实的,re-ioZh=ejorileror'e-in

线性相位 FIR 滤波器频率响应一般形式可写为 (e ) e ( ) j j( 0.5 ) =    H A - M  表 5-1 四种线性相位 FIR 滤波器的性质 类型 I II III IV 阶数 M 偶 奇 偶 奇 h[k]的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 奇对称 奇对称 偶对称 A()的周期 2 4 2 4  0 0 0.5 0.5 A 任意 任意 0 0 A 任意 0 0 任意 可适用的滤波器类型 LP,HP,B P,BS等 LP, BP 微分器,Hilbert 变换器 微分器,Hilbert 变换器，HP 表 5-1 四种线性相位 FIR 滤波器的性质 类型 I II III IV 阶数 M 偶 奇 偶 奇 h[k]的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 偶对称 奇对称 奇对称 表 5-1 四种线性相位 FIR 滤波器的性质 类型 I II III IV 阶数 M 偶 奇 偶 奇 h[k]的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 奇对称 奇对称 偶对称 A()的周期 2 4 2 4  0 0 0.5 0.5 A 任意 任意 0 0 A()关于=的对称性 偶对称 奇对称 奇对称 偶对称 A()的周期 2 4 2 4  0 0 0.5 0.5 A 任意 任意 0 0 A 任意 0 0 任意 可适用的滤波器类型 LP,HP,B P,BS等 LP, BP 微分器,Hilbert 变换器 微分器,Hilbert 变换器，HP 线性相位系统 H(z)的零点分布特性 h[k] = h[M − k] ( ) ( ) − −1  H z = z H z M • z=0 不可能有系统的零点 • zk 是系统的零点，则 zk-1 也是系统的零点。 • h[k]是实的, , k j k k z r e  = , k j k r e −  , 1 k j k r e − −  k j k r e −1  0 A ( ) 1  

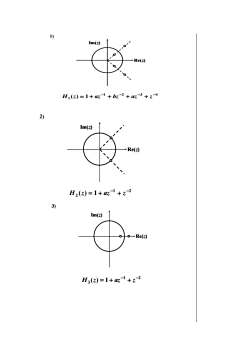
1)Im(z)Re(z)Hi(z) =1+ az-1 + bz-2 + az-3 + z-42)Im(z)+Re(z)H2(z) =1+ az-1 + z-23)Im(z)o-Re(z)?H3(z) =1+az- + z-2

1) 1 2 3 4 1 ( ) 1 − − − − H z =  az  bz  az  z Re(z) Im(z) Re(z) Im(z) 2) Re(z) Im(z) Re(z) Im(z) 1 2 2 ( ) 1 − − H z =  az  z Re(z) Im(z) Re(z) Im(z) 1 2 3 ( ) 1 − − H z =  az  z 3)

4)Im(z)+Re(z)H4(z) =1± z-1任意线性相位系统是上述四种子系统的组合·h[K]奇对称时，H(z)在z=1处一定有奇数阶零点。四种不同类型的线性相位系统在zk=±1的零点：(1)I型FIR滤波器(M为偶)：在zk-1和zk=-1无零点或者有偶数个零点。(2)II型FIR滤波器(M为奇）：在zk=-1有奇数个零点，在zk-1无零点或者有偶数个零点。(3)III型FIR滤波器(M为偶)：在zk=1和zk=-1有奇数个零点。(4)IV型FIR滤波器(M为奇)：在zk=1有奇数个零点，在zk--1无零点或者有偶数个零点

Re(z) Im(z) Re(z) Im(z) 4) 1 4 ( ) 1 − H z =  z •任意线性相位系统是上述四种子系统的组合 •h[k]奇对称时，H(z)在z=1处一定有奇数阶零点。 四种不同类型的线性相位系统在 zk=1 的零点： (1)I 型 FIR 滤波器(M 为偶)： 在 zk=1 和 zk= -1 无零点或者有偶数个零点。 (2)II 型 FIR 滤波器(M 为奇)： 在 zk= -1 有奇数个零点，在 zk=1 无零点或者有偶数个零点。 (3)III 型 FIR 滤波器(M 为偶)： 在 zk=1 和 zk= -1 有奇数个零点。 (4)IV 型 FIR 滤波器(M 为奇)： 在 zk=1 有奇数个零点，在 zk=-1 无零点或者有偶数个零点

5.2窗函数法设计FIR滤波器·最小积分平方误差设计FIR滤波器·吉伯斯(Gibbs)现象·常用窗函数窗函数法的MATLAB实现5.2.1最小积分平方误差设计FIR滤波器问题：已知Hd(ejW)，设计使其频率响应逼近Hd(ejW)。Th[k]-kH(-)=k=01T Ha(e)eind2h,[k]=-2元ha[K]一般情况下是无穷序列，需对其进行截断。方案1：设Ha(ei)是实偶函数，则ha[K]是实偶对称的。设 M=-2K, w[K]=RN+I[K]h [K]- ha [k-K]RN+1[K]h [M-k]= hd [M-k-M/2] RN+1 [K]= hd [-(k-N /2] RN+1 [K] = hd [k-M]RN+1[K] = h[K]例：设计一个线性相位的FIR滤波器。其频率响应能逼近截频为Wc的理想低通。[12≤2。解：设H(ej)=lo其他12eSa(2,k)f1.e/ dQ - -h,[k]-2元20元h[k]= h,[k- M /2]- α=sa(2,(k- M /2),0 ≤k≤ M2元方案2：设Ha(ej2)为Ha (ei?)=Ad(2)exp(i( -0.5MQ +b)I型和II:b=0III型和IV:b=元/2。h [K]= ha [K]RN+1[K]例：设计一个线性相位的FIR滤波器。其频率响应能逼近截频为Wc的理想低通。解：设j0.5M220≤H.(e其他0Sa(Q,(k - M /2)j0.5m.ejkndQ=h,[k] 2元元0

5.2 窗函数法设计 FIR 滤波器 • 最小积分平方误差设计 FIR 滤波器 • 吉伯斯(Gibbs)现象 • 常用窗函数 • 窗函数法的 MATLAB 实现 5.2.1 最小积分平方误差设计 FIR 滤波器 问题：已知 Hd(ejW)，设计 使其频率响应逼近 Hd(ejW)。 k M k H z h k z − = ( ) =  [ ] 0 =    −  ( ) d 2 1 [ ] j jk d d h k H e e    hd [k]一般情况下是无穷序列，需对其进行截断。 方案 1：设 Hd (ej  )是实偶函数， 则 hd [k]是实偶对称的。 设 M=2K, w[k]=RN+1[k] h [k]= hd [k-K]RN+1[k] h [M-k]= hd [M-k-M/2] RN+1 [k] = hd [-(k-N /2)] RN+1 [k] = hd [k-M]RN+1[k] = h[k] 例：设计一个线性相位的 FIR 滤波器。其频率响应能逼近截频 为 Wc 的理想低通。 解：设       =  0 其他 1 ( ) d j c H e 1 Sa( ) 2 1 h [k] e d kc jk c d c c   =   =   −    h k hd k M c c k − M   k  M  [ ] = [ − / 2] = Sa ( / 2 ,0  方案 2：设 Hd (ej  )为 Hd (ej  )=Ad(  )exp(j( -0.5M  +b)) I 型和 II: b=0 ; III 型和 IV:b= /2。 h [k]= hd [k]RN+1[k] 例：设计一个线性相位的 FIR 滤波器。其频率响应能逼近截频 为 Wc 的理想低通。 解：设        = −   0 其他 e 0 ( ) j0.5 d c M j H e e Sa ( / 2) 2 1 [ ] j0.5 h k e d c c k M M j k d c c  −  =   = −    −   

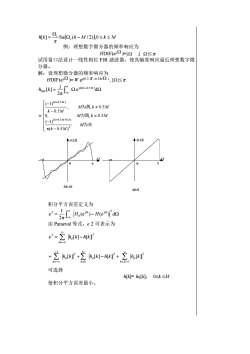
h[k)- 2cSa(2,(k-M /2),0≤k≤MT例：理想数字微分器的频率响应为HDIF(ej)j 试用窗口法设计一线性相位FIR滤波器，使其幅度响应逼近理想数字微分器。解：设理想微分器的频率响应为HDIF(e)We(0.5元-0.5M),[" Qejin(k-0.5M)dQhpr[k]=-2元／(-1)(k-0.5M)M为偶，k*0.5Mk-0.5MM为偶,k=0.5M=20(1)(k0.5M+0.5)M为奇元(k-0.5M)24A(2)A(2)LM-10M-9积分平方误差定义为- Md(en)-He)da由Parseval等式，e2可表示为”- 2 h[K]- [K]Z h,[Kk]+≥ h,[k]- [k]+Z (h,[k]"k=M+I可选择h[k]= ha[K],0<k≤M使积分平方误差最小

h k c c k − M   k  M  [ ] = Sa ( / 2) ,0  例：理想数字微分器的频率响应为 HDIF(e j  )=j  ,|  |  试用窗口法设计一线性相位 FIR 滤波器，使其幅度响应逼近理想数字微 分器。 解：设理想微分器的频率响应为 HDIF(ej  )= W e j(0.5  -0.5M  ) , |  |  =    − − e d 2π j [ ] j ( 0.5 ) π π DIF k M h k        =  − − =  − − −  − 为奇 为偶 为偶 M k M M k M M k M k M k M k M ( 0.5 ) ( 1) 0, , 0.5 , , 0.5 0.5 ( 1) 2 ( 0.5 0.5) ( 0.5 ) A()  −    − A()   = = 积分平方误差定义为 = −    − (e ) ( ) d 2π 1 2 j d π π 2 j  H H e 由 Parseval 等式，e 2 可表示为 2 2 h [k] h[k] d k =  −  =−  2 1 2 0 2 1 h [k] h [k] h[k] h [k] d k M d M k d k     = =  − =− =  −  可选择 h[k]= hd[k]， 0k M 使积分平方误差最小