《数字信号处理》课程教学课件（PPT讲稿）ch1_7 全通滤波器

全通滤波器与最小相位系统全通滤波器的定义一阶复系数全通滤波器m阶实系数全通系统·最小相位系统

全通滤波器与最小相位系统 •全通滤波器的定义 •一阶复系数全通滤波器 •m阶实系数全通系统 •最小相位系统

全通滤波器的定义定义：如果用Am(z)表示m阶实系数全通滤波器的系统函数，则幅度响应恒为常数的系统称为全通滤波器= Am(z)Am(zAm(z)Am (z-l) = 1

全通滤波器的定义 定义：如果用Am(z)表示m 阶实系数全通滤波器的系统函数，则幅 度响应恒为常数的系统称为全通滤波器 ( ) ( ) 1 1 = − A z A z m m ( ) ( ) ( ) 1 1 2 = = = −   j m m z e j m A e A z A z

阶复系数全通滤波器z-l-d[d|<1A(z)1 - dz-1a)一阶全通滤波器的极点和零点：关于单位圆镜像对称记: d = rej0Pi = d = rejo极点为：zi = 1 / d*= (1 / r)eje零点为：

一阶复系数全通滤波器 1 1 1 1 ( ) − −  − − = dz z d A z d 1 a)一阶全通滤波器的极点和零点：关于单位圆镜像对称 j 记：d = re 极点为： j p = d = re 1 零点为： j z 1/ d* (1/r)e 1 = =

A(-)2z-db一阶全通滤波器的频率响应1-dz=e-jo l-d*ejoe-j? -d*A(ej?) :1-de-jo1-de-j?A(ej?)=1A(ej)=e-jn l-re-joej?1-reje-jor sin(Ω-0)-1d(2) = -2-2 tan1-rcos(Ω-0)1-r2dp(2)<0dQ(1-r cos(Ω-0)2 +r2 sin (2-0)故一阶全通滤波器的相位响应是单调递减的

b)一阶全通滤波器的频率响应 1 1 1 1 ( ) − −  − − = dz z d A z    j j j de e d A e − −  − − = 1 ( ) 1    j j j de d e e −  − − − = 1 1 1 ( ) =1 j A e       j j j j j j re e re e A e e − − − − − = 1 1 ( ) 1 1 cos( ) sin( ) ( ) 2 tan 1        − − − = − − − r r 0 (1 cos( )) sin ( ) ( ) 1 2 2 2 2  − − + − − = −        r r r d d 故一阶全通滤波器的相位响应是单调递减的

m阶实系数全通系统+d,z-(m-1)-mz-mD,Iz-I+..(z-1m+c-7Am(z) =一m-(m-1)1+d,z-'+.+dmDm(z)Ca)m阶全通滤波器的极点和零点如z为一个极点，则*也是一个极点，1/zk和1/zk*必为系统零点，b）m阶全通滤波器的频率响应由于: A (2)4m(=")=="DMmDm(z)7Dm(z)D.(z-l)m= Am(z)Am(z-l)jo=1

m阶实系数全通系统 ( ) ( ) 1 ( ) 1 ( 1) 1 1 1 ( 1) 1 1 1 D z z D z d z d z d z d d z d z z A z m m m m m m m m m m m m − − − − − − − − − − − − = + + + + + + + + =   a)m阶全通滤波器的极点和零点 如zk为一个极点， 则zk * 也是一个极点, 1/zk和1/zk *必为系统零点。 b)m阶全通滤波器的频率响应 1 ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 = = − − − − D z z D z D z z D z A z A z m m m m M m 由于： m m ( ) ( ) ( ) 1 1 2 = = = −   j m m z e j m A e A z A z

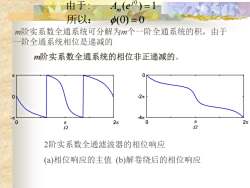
由于：Am（ej0)-l所以：d(0)=0m阶实系数全通系统可分解为m个一阶全通系统的积，由于一阶全通系统相位是递减的m阶实系数全通系统的相位非正递减的。O-2元0-4元002元2元元222阶实系数全通滤波器的相位响应(a)相位响应的主值(b)解卷绕后的相位响应

: ( ) 1 0 = j m 由于 A e 所以： (0) = 0 m阶实系数全通系统可分解为m个一阶全通系统的积，由于 一阶全通系统相位是递减的 m阶实系数全通系统的相位非正递减的。 2阶实系数全通滤波器的相位响应 (a)相位响应的主值 (b)解卷绕后的相位响应 0  2 - 0   0  2 -4 -2 0 

最小相位系统定义：零极点都在单位圆内的因果系统称为最小相位系统。记为Hmin(z)。任一实系数因果稳定系统的Hz）都可表示为H(z) = Hmin (z)Am(z)设系统H(z)只有一个零点在z=1/α*在单位圆外，la<1那么H(2）就能表示成H(z)=H()(z-1 - α*)按定义H(z)是一个最小相位系统。H(z)也可等效的表示为1az= H(z)(1-az-l) 二"-a"H(z) = H(z)(z-1 -αazaz故H(z) =Hmin(2) Ai(z)

最小相位系统 定义：零极点都在单位圆内的因果系统称为最小相 位系统。记为Hmin(z)。 任一实系数因果稳定系统的H(z)都可表示为 ( ) ( ) ( ) min H z H z A z = m 设系统H(z)只有一个零点在z = 1/a*在单位圆外，|a|<1， 那么H(z)就能表示成 H(z)=H1 (z)(z −1 − a*) 按定义H1 (z)是一个最小相位系统。H(z)也可等效的表示为 1 1 1 1 1 1 ( ) ( )( ) − − −  − − = − az az H z H z z a 1 1 1 1 1 ( )(1 ) − −  − − − = − az z a H z az 故 H(z) =Hmin(z) A1 (z)

例一实系数因果稳定系统的系统函数H为b+ 2-1, [a<1, b] <1H(z)1 + az由于系统的零点为z=一1/b，故这不是一最小相位系统1 + bz-1 b + z-1b + z-1 1 + bz-11H(z) :1 +az-l 1+ bz-11 + az-l 1 + bz-1和H2）具有相同幅度响应的最小相位系统为1 + bz-1H.i.(z)T1 + az-1

例 一实系数因果稳定系统的系统函数H(z)为 , 1, 1 1 ( ) 1 1   + + = − − a b az b z H z 由于系统的零点为z = −1/b，故这不是一最小相位系统。 1 1 1 1 1 1 1 ( ) − − − − + + + + = bz bz az b z H z 1 1 min 1 1 ( ) − − + + = az bz H z 1 1 1 1 1 1 1 − − − − + + + + = bz b z az bz 和H(z)具有相同幅度响应的最小相位系统为

最大相位系统（maximum-phasesystem）一个稳定的的因果系统，零点全在单位圆外

最大相位系统(maximum-phase system): 一个稳定的的因果系统，零点全在单位圆外