西安邮电学院：《数字电路与逻辑设计》课程教学资源（PPT课件）第一章 绪论

西安邮电学院“校级优秀课程”数字电路与逻辑设计第一章绪论西安郏电学院

数字电路与逻辑设计 第一章 绪 论 西安邮电学院“校级优秀课程

第一章绪论目的与要求：1、正确理解一些有关数字电路的基本概念；2、常用数制数的表示以及它们之间的转换；3、掌握数字系统中常用的几种BCD码。重点与难点：1、不同数制之间的相互转换；2、用BCD码表示十进制数3、算术运算与逻辑运算

第一章 绪 论 目的与要求： 1、正确理解一些有关数字电路的基本概念； 2、常用数制数的表示以及它们之间的转换； 3、掌握数字系统中常用的几种BCD码。 重点与难点： 1、不同数制之间的相互转换； 2、用BCD码表示十进制数； 3、算术运算与逻辑运算

Y第一章 绪论1.1.1数字信号1.1.2数制及其转换1.1.3二－十进制代码（BCD代码）1.1.4算术运算与逻辑运算1.1.5数字电路

第1章 绪 论 第一章 绪 论 1.1.1 数字信号 1.1.2 数制及其转换 1.1.3 二－十进制代码（BCD代码） 1.1.4 算术运算与逻辑运算 1.1.5 数字电路

第一章绪论1.1.1数字信号1·基本概念数字量：在时间上和数值都是离散的物理量，而且每次增减变化总是发生在一系列离散的瞬间，数量大小和每次的增减变化都是某一个最小单位的整数倍。数字信号：表示数字量的信号。数字电路：处理数字信号的电路回顾与思考：数字信号与模拟信号有何区别？模拟信号在时间上和数值上都具有连续变化的特点。在某一瞬间的值可以是一个数值区间内的任何值口西安鄂重学院

1.1.1 数字信号 １．基本概念 数字量：在时间上和数值都是离散的物理量，而且每次增减变 化总是发生在一系列离散的瞬间，数量大小和每次的增减变化 都是某一个最小单位的整数倍。 数字信号：表示数字量的信号。 数字电路：处理数字信号的电路。 模拟信号在时间上和数值上都具有连续变化的特点。在某一 瞬间的值可以是一个数值区间内的任何值。 回顾与思考：数字信号与模拟信号有何区别？ 第一章 绪 论

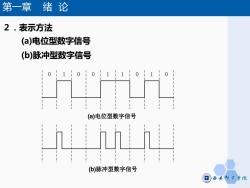
第一章绪论2．表示方法(a)电位型数字信号(b)脉冲型数字信号(a)电位型数字信号(b)脉冲型数字信号西安邸電学院

第一章 绪 论 ２．表示方法 (a)电位型数字信号 (b)脉冲型数字信号 0 (a)电位型数字信号 1 0 0 1 1 0 1 0 (b)脉冲型数字信号

1.1.2数制及其转换数制：按进位规则进行计数，称为进位计数制1.十进制数十进制数采用0、1、、9十个不同的数码；在计数时，采用“逢十进一”及“借一当十”。各个数码处于十进制数的不同数位时，代表的数值是不同的，这些数值称为位权。对于任意一个十进制数都可以按位权展开：(N)10 =an-1an-2 ...ajo.a-1a-2 ...a-m =an-1 ×10n-1 +an-2 ×10n-2 +...+a ×10' + ao ×10° +二a-1×10-1 +a-2×10-2 +.+a-m ×10-m = Za; ×10ii=-m式中，a为十进制数的任意一个数码；n、m为正整数，n表示整数部分数位，m表示小数部分数位。口西安哪電学院

１．十进制数 十进制数采用0、1、···、9十个不同的数码；在计数时， 采用“逢十进一”及“借一当十” 。各个数码处于十进制数的 不同数位时，代表的数值是不同的，这些数值称为位权。对于 任意一个十进制数都可以按位权展开： m m n n n n n n m a a a a a a a N a a a a a a a − − − − − − − − − − − − − − −  +  +  +   +  + +  +  + =   = 10 10 10 10 10 10 10 ( ) . 2 2 1 1 0 0 1 1 2 2 1 1 10 1 2 1 0 1 2  − =− =  1 10 n i m i ai 式中，ai为十进制数的任意一个数码；n、m为正整数，n表示 整数部分数位，m表示小数部分数位。 1.1.2 数制及其转换 数制：按进位规则进行计数，称为进位计数制

1.1.2 数制及其转换 十进制数按位权展开的方法，可以推广到任意进制的计数制。 对于一个基数为R(R2)的进制计数制，共有0、1、.、(R1) 个不同的数码，则一个进制的数按位权可展开为： (N)R=0n-14n-2.10.0-10-2.0-m= an-1×R”-+an-2×R”-2+.+a×Rl+0×R0+ a1XR+a2xR2++am×Rm=究4×R i-m 这种计数法叫做“进制”计数法，称为计数制的基数或 称为计数的模(mod)。在数W的表示中，用下角标或(mod=) 来标明模

十进制数按位权展开的方法，可以推广到任意进制的计数制。 对于一个基数为R(R≥2)的R进制计数制，共有0、1、···、(R-1) 个不同的数码，则一个R进制的数按位权可展开为： m m n n n n R n n m a R a R a R a R a R a R a R N a a a a a a a − − − − − − − − − − − − − − −  +  +  +   +  +  +  +  + =   = 2 2 1 1 0 0 1 1 2 2 1 1 1 2 1 0 1 2 ( ) .  − =− =  n 1 i m i ai R 这种计数法叫做“R进制”计数法，R称为计数制的基数或 称为计数的模(mod)。在数N 的表示中，用下角标或(mod=R) 来标明模。 1.1.2 数制及其转换

1.1.2 数制及其转换 .二进制数 2 二进制数只有0和1两个数码，在计数时“逢二进一”及“借一 当二”。二进制的基数是2，每个数位和位权值为2的幂。二进制 数可以按位权展开为： (N)2=0n-14n-2.10.0-10-2.0-m= -1×2n-1+an-2×2"-2++41×2l+0×20+ a1×21+a-2×22++a-m×2m=24×2 i=-m 式中，a为0或1数码；n、为正整数，2为位的位权值。 例如：(1101.01)2=1×23+1×22+0×2+1×2°+0×21+1×22

２．二进制数 二进制数只有0和1两个数码，在计数时“逢二进一”及“借一 当二” 。二进制的基数是2，每个数位和位权值为2的幂。二进制 数可以按位权展开为： m m n n n n n n m a a a a a a a N a a a a a a a − − − − − − − − − − − − − − −  +  +  +   +  +  +  +  + =   = 2 2 2 2 2 2 2 ( ) . 2 2 1 1 0 0 1 1 2 2 1 1 2 1 2 1 0 1 2  − =− =  1 2 n i m i ai 式中，ai为0或1数码；n、m为正整数，2 i为i位的位权值。 3 2 1 0 1 2 (1101.01)2 1 2 1 2 0 2 1 2 0 2 1 2 − − 例如： =  +  +  +  +  +  1.1.2 数制及其转换

1.1.2 数制及其转换 3.八进制和十六进制 八进制数有0~7八个数码，基数为8，八进制数表示为： - (N)8= i=-m 例如：(16.4公=1×82+6×8°+4×81 十六进制数有0~9、A~F十六个数码符号，其中A~F六个 符号依次表示10~15。 n-l (N)16=∑a4;×16 i=-m 例如：(A6.C6=10×16+6×16°+12×16 重学院

 − =− =  1 ( )8 8 n i m i N ai 1 0 1 例如： (16.4)8 1 8 6 8 4 8 − =  +  +  ３．八进制和十六进制 八进制数有0～7八个数码，基数为8，八进制数表示为： 十六进制数有0～9、A～F十六个数码符号，其中A～F六个 符号依次表示10～15。  − =− =  1 ( )16 16 n i m i N ai 1 0 1 例如： (A6.C)1 6 1 0 1 6 6 1 6 1 2 1 6− =  +  +  1.1.2 数制及其转换

1.1.2 数制及其转换 4.不同进制数的转换 (1)将进制数转换成十进制数 将进制数转换为等值的十进制数，只要将进制数按位权 展开，再按十进制运算规则运算即可。 例1：将下列各进制数转换成十进制数。 (D8.A)16=13×161+8×160+10×16-1 =(216.625)10 (207.04)8=2×82+0×81+7×80+0×8-1+4×8-2 =(135.0625)10 (101.01)2=1×22+0×21+1×20+0×2-1+1×2-2 =(5.25)10

４．不同进制数的转换 (1) 将R进制数转换成十进制数 将R进制数转换为等值的十进制数，只要将R进制数按位权 展开，再按十进制运算规则运算即可。 例1：将下列各进制数转换成十进制数。 (D8.A)16＝ 13×161 ＋8×160＋10×16－1 ＝(216.625)10 (207.04)8＝ 2×8 2 ＋0×8 1＋7×8 0＋0×8－1＋4 ×8－2 ＝(135.0625)10 (101.01)2＝ 1×2 2 ＋0×2 1＋1×2 0＋0×2－1＋1 ×2－2 ＝(5.25)10 1.1.2 数制及其转换