西安邮电学院：《数字电路与逻辑设计》课程教学资源（PPT课件）第二章 逻辑函数及其简化

■■■ 西安邮电学院“校级优秀课程” 3 数字电路与逻辑设计 第二章逻辑函数及其简化 安郎電学院

数字电路与逻辑设计 第二章 逻辑函数及其简化 西安邮电学院“校级优秀课程

第二章逻辑函数及其简化 2.1逻辑代数 2.2逻辑函数的简化 8

第二章 逻辑函数及其简化 2.1 逻辑代数 2.2 逻辑函数的简化

第二章 逻辑函数及其简化 2.1.1 基本逻辑 2.1.2 基本逻辑运算 2.1.3 真值表与逻辑函数 2.1.4 逻辑代数的基本定律 2.1.5 三个规则 2.1.6 常用公式 2.1.7 逻辑函数的标准形式 ⊙西安邹重拳院

2.1.1 基本逻辑 2.1.2 基本逻辑运算 2.1.3 真值表与逻辑函数 2.1.4 逻辑代数的基本定律 2.1.5 三个规则 2.1.6 常用公式 2.1.7 逻辑函数的标准形式 第二章 逻辑函数及其简化

2.1 逻辑代数 2.1.1基本逻辑 1·与、或、非三种基本逻辑关系 (1)与逻辑关系 与逻辑关系：只有当决定某一事件的条件全部具备 时，这一事件才会发生。 与逻辑举例状态表 S2 开关S, 开关S2 灯 电源 ☒灯 断 断 灭 断 合 灭 合 断 灭 与逻辑举例 合 合 亮 8西安重学院

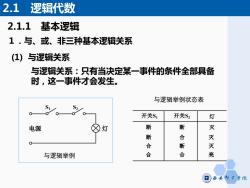
2.1 逻辑代数 2.1.1 基本逻辑 １．与、或、非三种基本逻辑关系 (1) 与逻辑关系 S1 S2 与逻辑举例 电源 灯 与逻辑举例状态表 开关S1 开关S2 灯 断 断 灭 断 合 灭 合 合 断 灭 合 亮 与逻辑关系：只有当决定某一事件的条件全部具备 时，这一事件才会发生

2.1 逻辑代数 (2) 或逻辑关系 或逻辑关系：只要在决定某一事件的各种条件中，有一个 或几个条件具备时，这一事件就会发生。 或逻辑举例状态表 开关S 开关S2 灯 Q 电源 ⑧灯 断 断 灭 断 合 亮 合 断 亮 或逻辑举例 合 合 亮

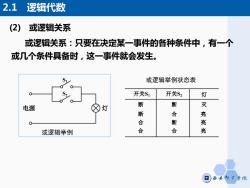
(2) 或逻辑关系 2.1 逻辑代数 或逻辑关系：只要在决定某一事件的各种条件中，有一个 或几个条件具备时，这一事件就会发生。 S1 电源 灯 或逻辑举例 S2 或逻辑举例状态表 开关S1 开关S2 灯 断 断 灭 断 合 亮 合 合 断 亮 合 亮

2.1 逻辑代数 (3) 非逻辑关系 非逻辑关系：事件发生的条件具备时，事件不会发生；事 件发生的条件不具备时，事件发生。 非逻辑举例状态表 Q 电源 灯 开关s 灯 断 亮 非逻辑举例 合 灭 ⊙西邹重学院

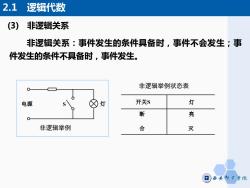
(3) 非逻辑关系 2.1 逻辑代数 非逻辑关系：事件发生的条件具备时，事件不会发生；事 件发生的条件不具备时，事件发生。 灯 非逻辑举例 电源 非逻辑举例状态表 开关S 灯 断 亮 合 灭

2.1 逻辑代数 2.基本逻辑关系在逻辑代数中的描述 (1)真值表描述法 真值表：用状态变量和取值可以列出表示三种基本逻辑关系的 图表。在逻辑代数中用字母表示逻辑变量，逻辑变量在二值逻 辑中只有0和1两种取值，以代表两种不同的逻辑状态。 与逻辑真值表 或逻辑真值表 非逻辑真值表 B P B P A 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 0 0 1 0 1 1 1 1

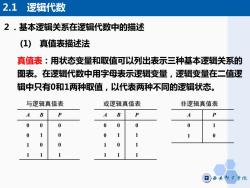
２．基本逻辑关系在逻辑代数中的描述 2.1 逻辑代数 (1) 真值表描述法 真值表：用状态变量和取值可以列出表示三种基本逻辑关系的 图表。在逻辑代数中用字母表示逻辑变量，逻辑变量在二值逻 辑中只有0和1两种取值，以代表两种不同的逻辑状态。 与逻辑真值表 或逻辑真值表 非逻辑真值表 A B P 0 0 1 0 1 0 1 1 0 0 0 1 A B P 0 0 1 0 1 0 1 1 0 1 1 1 A P 0 1 1 0

2.1 逻辑代数 (2) 数学表达式描述法 与逻辑：P=A·B 又称为与运算或逻辑乘。 运算符。若不致混淆，可省略。 或逻辑：P=A+B 又称为或运算或逻辑加。 非逻辑：P=A 读作“A非”或“非A

2.1 逻辑代数 (2) 数学表达式描述法 与逻辑： P = A ·Ｂ 又称为与运算或逻辑乘。 运算符。若不致混淆，可省略。 或逻辑： P = A +Ｂ 又称为或运算或逻辑加。 非逻辑： P = A 读作“A非” 或“非A”

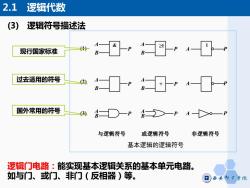
2.1 逻辑代数 (3) 逻辑符号描述法 现行国家标准 A图-pA可-4巴一 过去适用的符号 2 A☐g阳4口 国外常用的符号 与逻辑符号 或逻辑符号 非逻辑符号 基本逻辑的逻辑符号 逻辑门电路：能实现基本逻辑关系的基本单元电路。 如与门、或门、非门（反相器）等

2.1 逻辑代数 (3) 逻辑符号描述法 (1) (2) (3) A B + P A B P A ≥1 1 P A B P A B P A P & A B P A P 基本逻辑的逻辑符号 与逻辑符号 或逻辑符号 非逻辑符号 A B P 现行国家标准 过去适用的符号 国外常用的符号 逻辑门电路：能实现基本逻辑关系的基本单元电路。 如与门、或门、非门（反相器）等

2.1逻辑代数 2.1.2 基本逻辑运算 1.逻辑加（或运算) P=A+B 运算规则： 0+0=0 一般形式：A+0=A 0+1=1 A+1=1 1+0=1 4+4=4 1+1=1 2.逻辑乘（与运算） P=A·B 运算规则：0·0=0 一般形式：A·1=A 0·1=0 A·0=0 1·0=0 A·A=A 1·1=1

2.1 逻辑代数 2.1.2 基本逻辑运算 １．逻辑加（或运算） P = A +Ｂ 运算规则： 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1 一般形式： A + 0 = A A + 1 = 1 A + A = A ２．逻辑乘（与运算） P = A ·Ｂ 运算规则： 0 · 0 = 0 0 · 1 = 0 1 · 0 = 0 1 · 1 = 1 一般形式： A · 1 = A A · 0 = 0 A · A = A