《计量经济学》课程授课教案（讲稿）06 异方差

1.5假定条件的不成立用OLS法得到的估计模型通过统计检验后，还要检验模型是否满足假定条件。由1.3节知，只有模型的4个假定条件都满足时，用OLS法得到的估计量才具有最佳线性无偏特性。当一个或多个假定条件不成立时，OLS估计量将丧失上述特性。本节讨论当假定条件不成立时，对参数估计带来的影响以及相应的补救措施。以下讨论都是在某一个假定条件被违反，而其他假定条件都成立的情况下进行。分为5个步骤。（1）回顾假定条件。（2）假定条件不成立对模型参数估计带来的影响。（3）定性分析假定条件是否成立。（4）假定条件是否成立的检验（定量判断）。（5）假定条件不成立时的补救措施。1.5.1同方差假定1225L10-20.8...15610a:A52featsea~o:"x+2550100200o150050100150200图5.1同方差情形图5.2同方差情形模型的假定条件(1）给出Var(u）是一个对角矩阵，07[11Var(u) = E(uu')= "[= g(5.1)-LO1且u的方差协方差矩阵主对角线上的元素都是常数且相等，即每一误差项的方差都是有限的相同值（同方差假定）：且非主对角线上的元素为零（非自相关假定），当这个假定不成立时，Var(u）不再是一个纯量对角矩阵。00[ou0022Var(u)=2Q=2*o?1(5.2)Lo0.o当误差向量u的方差协方差矩阵主对角线上的元素不相等时，称该随机误差系列存在异方差，即误差向量u中的元素u，取自不同的分布总体。非主对角线上的元素表示误差项之间的协方差值。比如Q中的i与α的乘积，（i+j）表示与第i组和第组观测值相对应的u与u的协方差。若Q非主对角线上的部分或全部元素都不为零，误差项就是自相关的。1

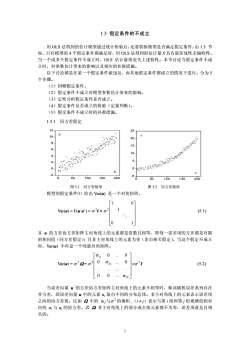
1.5 假定条件的不成立 用 OLS 法得到的估计模型通过统计检验后，还要检验摸型是否满足假定条件。由 1.3 节 知，只有模型的 4 个假定条件都满足时，用 OLS 法得到的估计量才具有最佳线性无偏特性。 当一个或多个假定条件不成立时，OLS 估计量将丧失上述特性。本节讨论当假定条件不成 立时，对参数估计带来的影响以及相应的补救措施。 以下讨论都是在某一个假定条件被违反，而其他假定条件都成立的情况下进行。分为 5 个步骤。 （1）回顾假定条件。 （2）假定条件不成立对模型参数估计带来的影响。 （3）定性分析假定条件是否成立。 （4）假定条件是否成立的检验（定量判断）。 （5）假定条件不成立时的补救措施。 1.5.1 同方差假定 -2 0 2 4 6 8 10 12 0 50 100 150 200 X Y 图 5.1 同方差情形 图 5.2 同方差情形 模型的假定条件⑴ 给出 Var(u) 是一个对角矩阵， Var(u) = E(u u') = σ 2 I = σ 2 1 0 1 0 1 ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ % (5.1) 且 u 的方差协方差矩阵主对角线上的元素都是常数且相等，即每一误差项的方差都是有限 的相同值（同方差假定）；且非主对角线上的元素为零（非自相关假定），当这个假定不成立 时，Var(u) 不再是一个纯量对角矩阵。 Var(u) = σ 2 Ω = σ 2 ≠σ 2 I (5.2) 11 22 0 . 0 0 . . . . . 0 0 . TT σ σ σ ⎡ ⎤ ⎢ ⎥ ⎢ ⎢ ⎥ ⎣ ⎦ 0 ⎥ 当误差向量 u 的方差协方差矩阵主对角线上的元素不相等时，称该随机误差系列存在 异方差，即误差向量 u 中的元素 ut 取自不同的分布总体。非主对角线上的元素表示误差项 之间的协方差值。比如 Ω 中的 σi j与σ 2 的乘积 ,（i ≠ j）表示与第 i 组和第 j 组观测值相对 应的 ui 与 uj 的协方差。若 Ω 非主对角线上的部分或全部元素都不为零，误差项就是自相 关的。 1

本节讨论异方差。下一节讨论自相关问题。以两个变量为例，同方差假定如图5.1和5.2所示。对于每一个x值，相应u的分布方差都是相同的。152异方差表现与来源异方差通常有三种表现形式，（1）递增型，（2）递减型，（3）条件自回归型。递增型异方差见图5.3和5.4。图5.5为递减型异方差。图5.6为条件自回归型异方差。Y6./5-d320406080100*120140160180260图5.3递增型异方差情形图5.4递增型异方差-680.TTT700800900100011001200400500600501001500200图5.5递减型异方差图5.6复杂型异方差（1）时间序列数据和截面数据中都有可能存在异方差。(2）经济时间序列中的异方差常为递增型异方差。金融时间序列中的异方差常表现为自回归条件异方差。无论是时间序列数据还是截面数据。递增型异方差的来源主要是因为随着解释变量值的增大，被解释变量取值的差异性增大。1.2E+1.2E+12RESID1.0E+12GDP of Phiippin8.0E+108.0E+114.0F+6.0E+11.M0.0E+4.0E+11-4.0E+1020E+110.0E+008.0E8486889092949698000284868890929496980002图5.7菲律宾的季度数据图5.8剔出2次趋势后的残差序列1.5.3异方差的后果下面以简单线性回归模型为例讨论异方差对参数估计的影响。对模型2

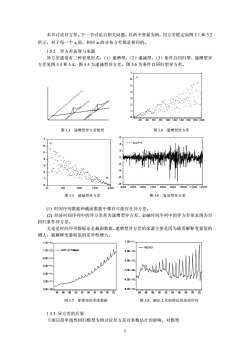
本节讨论异方差。下一节讨论自相关问题。以两个变量为例，同方差假定如图 5.1 和 5.2 所示。对于每一个 xt 值，相应 ut 的分布方差都是相同的。 1.5.2 异方差表现与来源 异方差通常有三种表现形式，（1）递增型，（2）递减型，（3）条件自回归型。递增型异 方差见图 5.3 和 5.4。图 5.5 为递减型异方差。图 5.6 为条件自回归型异方差。 0 1 2 3 4 5 6 7 20 40 60 80 100 120 140 160 180 200 Y 图 5.3 递增型异方差情形 图 5.4 递增型异方差 0 1 2 3 4 5 6 7 0 50 100 150 200 X Y -8 -6 -4 -2 0 2 4 6 400 500 600 700 800 900 1000 1100 1200 DJPY 图 5.5 递减型异方差 图 5.6 复杂型异方差 (1) 时间序列数据和截面数据中都有可能存在异方差。 (2) 经济时间序列中的异方差常为递增型异方差。金融时间序列中的异方差常表现为自 回归条件异方差。 无论是时间序列数据还是截面数据。递增型异方差的来源主要是因为随着解释变量值的 增大，被解释变量取值的差异性增大。 0.0E+00 2.0E+11 4.0E+11 6.0E+11 8.0E+11 1.0E+12 1.2E+12 84 86 88 90 92 94 96 98 00 02 GDP of Philippin -8.0E+10 -4.0E+10 0.0E+00 4.0E+10 8.0E+10 1.2E+11 84 86 88 90 92 94 96 98 00 02 RESID 图 5.7 菲律宾的季度数据 图 5.8 剔出 2 次趋势后的残差序列 1.5.3 异方差的后果 下面以简单线性回归模型为例讨论异方差对参数估计的影响。对模型 2

yr=B+ βix,+u当Var(u)=o,，为异方差时（o2是一个随时间或序数变化的量），回归参数估计量仍具有无偏性和一致性。以β,为例E(A)-E(2-00-)-E(2Z(x, -x)[β(x, -对)+u,],E(x, -x)2E(x, -x)2Z(,-7)E(u) =β=B+E(x, -x)2在上式的推导中利用了E(u）=0的假定。但是回归参数估计量不再具有有效性。仍以β为例，E(x,-x)u )((E(x, -x)u))Var (β,)= E(β,-β) =E=E((,-))=(x,-))q?Z(, -对)’E(u,)2_Z(x, -对)2 +(Z(x, -x)2)2(2(x, -x)2)2 +Z(x,-对)2（在上式的推导中利用了u的非自相关假定、x与u非相关假定）。上式不等号右侧项分子中的，不是一个常量，不能从累加式中提出，所以不等号右侧项不等于不等号左侧项。而不等号右侧项是同方差条件下β的最小二乘估计量β，的方差。因此异方差条件下的β失去有效性。另外回归参数估计量方差的估计是真实方差的有偏估计量。例如E(Var(B,)Var(β,)（证明略）下面用矩阵形式讨论。因为OLS估计量无偏性的证明只依赖于模型的一阶矩，所以当Var(u）如（5.2）式所示时，OLS估计量β仍具有无偏性和一致性。E(β)=E[(X"X)"X'Y)=E[(X'X)"X'(Xβ+u)]=β+(X"X)"X'E(u)=β但不具有有效性和渐近有效性。而且β的分布将受到影响。Var(β)=E[(β-β)(β-β)j=E[(XXx)"x"uuX(X'x)"]=(X"X)'X"E(uu)X(X"X)"= G"(X"X)"X"QX(X"X)不等于α(XX），所以异方差条件下β是非有效估计量。1.5.4异方差检验1.5.4.1定性分析异方差（1）经济变量规模差别很大时容易出现异方差。如个人收入与支出关系，投入与产出关系。3

yt = β0 + β1 xt + ut 当 Var(ut) = σt 2 ，为异方差时（σt 2 是一个随时间或序数变化的量），回归参数估计量仍具有 无偏性和一致性。以 为例 1 ˆ β E( )= E( 1 ˆ β ∑ ∑ − −− 2 )( ))(( xx yyxx t tt ) = E( ∑ ∑ − − +− 2 1 )( ])()[( xx uxxxx t t β t t ) = β1 + ∑ ∑ − − 2 )( )()( xx uExx t t t = β1 在上式的推导中利用了 E(ut) = 0 的假定。 但是回归参数估计量不再具有有效性。仍以 β ˆ 1为例， Var ( ) = E( -β1) 2 β ˆ 1 β ˆ 1 = E 2 2 ( ) ( ) t t t x x u x x ⎛ ⎞ − ⎜ ⎟ − ⎝ ⎠ ∑ ∑ = E 2 2 2 ( ( )) ( ( )) t t t x xu x x ⎛ ⎞ − ⎜ ⎟ − ⎝ ⎠ ∑ ∑ = ∑ ∑ − − 22 22 ))(( )(E)( xx uxx t t t = ∑ ∑ − − 22 2 2 ))(( )( xx xx t t σ t ≠ ∑ − 2 2 xx )( t σ （在上式的推导中利用了 ut 的非自相关假定、xt与 ut 非相关假定）。上式不等号右侧项分子 中的σt 2 不是一个常量，不能从累加式中提出，所以不等号右侧项不等于不等号左侧项。而 不等号右侧项是同方差条件下β1 的最小二乘估计量 的方差。因此异方差条件下的 失去 有效性。 1 ˆ β 1 ˆ β 另外回归参数估计量方差的估计是真实方差的有偏估计量。例如 E( ( )) ≠ Var ( ) ∧ Var 1 ˆ β 1 ˆ β （证明略） 下面用矩阵形式讨论。因为 OLS 估计量无偏性的证明只依赖于模型的一阶矩，所以当 Var(u) 如（5.2）式所示时，OLS 估计量 β ˆ 仍具有无偏性和一致性。 E( ) = E[ (X 'X ) -1 X 'Y ] = E[ (X 'X ) -1 X ' (X β + u) ] = β + (X 'X) -1 β X ' E(u) = β ˆ 但不具有有效性和渐近有效性。而且 的分布将受到影响。 β ˆ Var( ) = E [( - β ) ( - β )' ] = E [(X 'X ) -1 X ' u u' X (X 'X) -1 β ] ˆ β ˆ β ˆ = (X ' X) -1 X ' E (u u') X (X ' X ) -1 = σ 2 (X 'X ) -1 X ' Ω X (X ' X ) -1 不等于σ 2 (X ' X ) -1，所以异方差条件下 是非有效估计量。 β ˆ 1.5.4 异方差检验 1.5.4.1 定性分析异方差 (1) 经济变量规模差别很大时容易出现异方差。如个人收入与支出关系，投入与产出关 系。 3

(2)利用散点图做初步判断。(3）利用残差图做初步判断。6.25.4.3.-12-2 .T204060801001201401601802005015020001001.5.4.2异方差检验(1)White检验White检验由H.White1980年提出。Goldfeld-Quandt检验必须先把数据按解释变量的值从小到大排序。Gleiser检验通常要试拟合多个回归式。White检验不需要对观测值排序，也不依赖于随机误差项服从正态分布，它是通过一个辅助回归式构造统计量进行异方差检验。White检验的具体步骤如下。以二元回归模型为例，(5.9)y=+βx+x+ut①首先对上式进行OLS回归，求残差i，。②做如下辅助回归式，a,= do +aiXn +2 Xe + as xi? +a4 x? + asXn Xe + V(5.10)即用i对原回归式中的各解释变量、解释变量的平方项、交叉积项进行OLS回归。注意，上式中要保留常数项。求辅助回归式（5.10)的可决系数R。③White检验的零假设和备择假设是Ho:(5.9)式中的u不存在异方差，H：(5.9)式中的u存在异方差。④在不存在异方差假设条件下，统计量TR?~x°6)(5.11)其中T表示样本容量，R是辅助回归式(5.10)的OLS估计式的可决系数。自由度5表示辅助回归式(5.10)中解释变量项数（注意，不计算常数项）。TR2属于LM统计量。③判别规则是若TR2≤α(5),接受Ho（u具有同方差）若TR2>a(5,拒绝Ho（u具有异方差)附录：White检验的EViwes操作。在回归式窗口中点击View键选ResidualTests/WhiteHeteroskedasticity功能。检验式存在有无交叉项两种选择。(2) Goldfeld-Quandt 检验Ho:ut具有同方差，Hi:ut具有递增型异方差。4

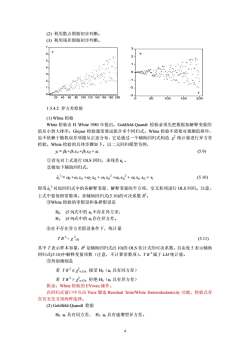
(2) 利用散点图做初步判断。 (3) 利用残差图做初步判断。 0 1 2 3 4 5 6 7 20 40 60 80 100 120 140 160 180 200 Y -3 -2 -1 0 1 2 3 0 50 100 150 200 T Y 1.5.4.2 异方差检验 (1) White 检验 White 检验由 H. White 1980 年提出。Goldfeld-Quandt 检验必须先把数据按解释变量的 值从小到大排序。Glejser 检验通常要试拟合多个回归式。White 检验不需要对观测值排序， 也不依赖于随机误差项服从正态分布，它是通过一个辅助回归式构造 χ 2 统计量进行异方差 检验。White 检验的具体步骤如下。以二元回归模型为例， yt = β0 +β1 xt1 +β2 xt2 + ut (5.9) ①首先对上式进行 OLS 回归，求残差 。ut ˆ ②做如下辅助回归式， 2 ˆut = α0 +α1 xt1 +α2 xt2 + α3 xt1 2 +α4 xt2 2 + α5 xt1 xt2 + vt (5.10) 即用 对原回归式中的各解释变量、解释变量的平方项、交叉积项进行 OLS 回归。注意， 上式中要保留常数项。求辅助回归式(5.10)的可决系数 R2 。 2 ˆut ③White 检验的零假设和备择假设是 H0: (5.9)式中的 ut不存在异方差， H1: (5.9)式中的 ut存在异方差。 ④在不存在异方差假设条件下，统计量 T R 2 ∼ χ 2 (5) (5.11) 其中 T 表示样本容量，R2 是辅助回归式(5.10)的 OLS 估计式的可决系数。自由度 5 表示辅助 回归式(5.10)中解释变量项数（注意，不计算常数项）。T R 2属于 LM 统计量。 ⑤判别规则是 若 T R 2 ≤ χ 2 α (5), 接受 H0（ut 具有同方差） 若 T R 2 > χ 2 α (5), 拒绝 H0（ut 具有异方差） 附录：White 检验的 EViwes 操作。 在回归式窗口中点击 View 键选 Residual Tests/White Heteroskedasticity 功能。检验式存 在有无交叉项两种选择。 (2) Goldfeld-Quandt 检验 H0: ut 具有同方差， H1: ut 具有递增型异方差。 4

构造F统计量。把原样本分成两个子样本。具体方法是把成对（组）的观测值按解释变量的大小顺序排列，略去m个处于中心位置的观测值（通常T>30时，取m~T/4，余下的T-m个观测值自然分成容量相等，（T-m)/2，的两个子样本。）(X1, X2,Xi-1, Xj, X+1,XT-I,XT)→n;=(T-m) /2m=T/4nz=(T-m)/2②用两个子样本分别估计回归直线，并计算残差平方和。相对于n2和ni分别用SSE2和SSE表式。③F统计量是SSE2SSE2 /(n2-k)F=（k为模型中被估参数个数）SSE, /(n) -k)SSE,在Ho成立条件下，F~F(m2-k,nl-k)>6.: YY"654.>3.3-2.xX50150200C100502000100150④判别规则如下，若F≤Fα(mn2-kml-K)，接受Ho（ut具有同方差）若F>Fα(n2-k,ml-k)，拒绝Ho（递增型异方差）注意：①当摸型含有多个解释变量时，应以每一个解释变量为基准检验异方差。②此法只适用于递增型异方差。③对于截面样本，计算F统计量之前，必须先把数据按解释变量的值从小到大排序。（3）Glejser检验检验Ii,I是否与解释变量x存在函数关系。若有，则说明存在异方差；若无，则说明不存在异方差。通常应检验的几种形式是[u,[=ao+axrIu, [= do + a x?lu,/=ao+ai/x,,Glejser检验的特点是：①既可检验递增型异方差，也可检验递减型异方差。②一旦发现异方差，同时也就发现了异方差的具体表现形式。③计算量相对较大。?当原模型含有多个解释变量值时，可以把1i,I拟合成多变量回归形式。(4）自回归条件异方差（ARCH）检验5

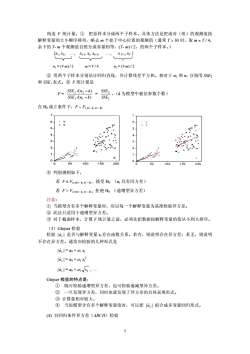
构造 F 统计量。① 把原样本分成两个子样本。具体方法是把成对（组）的观测值按 解释变量的大小顺序排列，略去 m 个处于中心位置的观测值（通常 T > 30 时，取 m ≈ T / 4， 余下的 T- m 个观测值自然分成容量相等，(T- m) / 2，的两个子样本。） {x1, x2, ., xi-1, xi, xi+1, ., x T-1, xT } n1 = (T-m) / 2 m = T / 4 n2 = (T-m) / 2 ② 用两个子样本分别估计回归直线，并计算残差平方和。相对于 n2 和 n1 分别用 SSE2 和 SSE1 表式。③ F 统计量是 F = )/( )/( 11 22 knSSE knSSE − − = 1 2 SSE SSE ，（k 为模型中被估参数个数） 在 H0 成立条件下，F ∼ F( n2 - k, n1 - k) 0 1 2 3 4 5 6 7 0 50 100 150 200 X Y Y ④ 判别规则如下， 若 F ≤ Fα (n2 - k, n1 - k) , 接受 H0 （ut 具有同方差） 若 F > Fα (n2 - k, n1 - k) , 拒绝 H0 （递增型异方差） 注意： ① 当摸型含有多个解释变量时，应以每一个解释变量为基准检验异方差。 ② 此法只适用于递增型异方差。 ③ 对于截面样本，计算 F 统计量之前，必须先把数据按解释变量的值从小到大排序。 （3）Glejser 检验 检验 | | 是否与解释变量 xt 存在函数关系。若有，则说明存在异方差；若无，则说明 不存在异方差。通常应检验的几种形式是 ut ˆ | ut | = a0 + a1 xt ˆ | | = a0 + a1 xt 2 ut ˆ | | ut = a0 + a1 ˆ t x , . Glejser 检验的特点是： ① 既可检验递增型异方差，也可检验递减型异方差。 ② 一旦发现异方差，同时也就发现了异方差的具体表现形式。 ③ 计算量相对较大。 ④ 当原模型含有多个解释变量值时，可以把 | uˆt | 拟合成多变量回归形式。 (4) 自回归条件异方差（ARCH）检验 5

异方差的另一种检验方法称作自回归条件异方差（ARCH）检验。这种检验方法不是把原回归模型的随机误差项看作是x的函数，而是把看作误差滞后项u-？，ut-2的函数。ARCH是误差项二阶矩的自回归过程。恩格尔（Engle1982）针对ARCH过程提出LM检验法。辅助回归式定义为i,?=o+α i +..+an i-n?(5.12).LM统计量定义为ARCH=TR2~×(m)其中R2是辅助回归式（5.12）的可决系数。在Ho：αi=...=αn=0成立条件下，ARCH渐近服从(m）分布。ARCH检验的最常用形式是一阶自回归模型（n=1)u,2= 0o + α1 u,-?在这种情形下，ARCH渐近服从）分布。1.5.5.克服异方差的方法克服异方差的矩阵描述。设模型为Y=Xβ+u其中E(u)=0，Var(u)=E(uu)=Q。Q已知，β与k未知。因为Q+I,违反了假定条件，所以应该对模型进行适当修正。因为Q是一个T阶正定矩阵，所以必存在一个非退化TxT阶矩阵M使下式成立。MQM'=ITxT从上式得M'M=Q-I用M左乘上述回归模型两侧得MY=MXβ+Mu取y*=MYX*=MX,u*=Mu，上式变换为Y* =X*β+ u*则u*的方差协方差矩阵为Var(u*)=E(u*u*")=E(MuuM')=M"QM="MQM'=α"I变换后模型的Var(u*)是一个纯量对角矩阵。对变换后模型进行OLS估计，得到的是β的最佳线性无偏估计量。这种估计方法称作广义最小二乘法。β的广义最小二乘（GLS）估计量定义为β(GLS)=(X*"X*)"X*"Y*=(X'M"MX)"X'M'MY=(X'Q"X)"X'Q"'Y（1）对模型(5.15)yr=B+Bixn+Ba+u通常假定异方差形式是Var(u)=(xa)。（因为Var(u)=E(u)2，相当于认为[i,/=αxi）用x同除上式两侧得_Bo + β+Bx2 +u,福(5.16)XXXX6

异方差的另一种检验方法称作自回归条件异方差 (ARCH) 检验。这种检验方法不是把 原回归模型的随机误差项σt 2 看作是 xt 的函数，而是把σt 2 看作误差滞后项 ut-1 2 , ut-2 2 , . 的函数。ARCH 是误差项二阶矩的自回归过程。恩格尔（Engle 1982）针对 ARCH 过程提出 LM 检验法。辅助回归式定义为 2 ˆut = α0 + α1 + . + α n (5.12) 2 1 ˆut− 2 ˆu −nt LM 统计量定义为 ARCH = T R 2 ∼ χ 2 (n) 其中 R 2 是辅助回归式（5.12）的可决系数。在 H0：α1 = . = αn = 0 成立条件下，ARCH 渐 近服从 χ 2 (n) 分布。ARCH 检验的最常用形式是一阶自回归模型（n = 1）， = α0 + α1 2 ˆut 2 1 ˆut− 在这种情形下，ARCH 渐近服从 χ 2 (1) 分布。 1.5.5. 克服异方差的方法 克服异方差的矩阵描述。设模型为 Y = X β + u 其中 E(u) = 0，Var(u) = E(u u') = σ 2 Ω。Ω 已知，β 与 k 未知。因为 Ω ≠ I，违反了假定条 件，所以应该对模型进行适当修正。 因为 Ω 是一个 T 阶正定矩阵，所以必存在一个非退化 T×T 阶矩阵 M 使下式成立。 M Ω M ' = I T×T 从上式得 M 'M = Ω-1 用 M 左乘上述回归模型两侧得 M Y = M X β + M u 取 Y* = M Y, X * = M X, u* = M u , 上式变换为 Y* = X*β + u* 则 u* 的方差协方差矩阵为 Var(u*) = E(u* u*' ) = E (M u u' M ') = M σ 2 Ω M ' = σ 2 M Ω M ' = σ 2 I 变换后模型的 Var(u*)是一个纯量对角矩阵。对变换后模型进行 OLS 估计，得到的是 β 的最佳线性无偏估计量。这种估计方法称作广义最小二乘法。β 的广义最小二乘 (GLS) 估 计量定义为 (GLS) = (X*' X*)-1 X*' Y* = (X 'M ' M X ) -1 X ' M 'M Y = (X 'Ω-1X) -1 X 'Ω-1 β Y ˆ （1）对模型 yt = β0 + β1 xt1 + β2 xt2 + ut (5.15) 通常假定异方差形式是 Var(ut) = (σ xt1) 2 。（因为 Var(ut) = E(ut) 2 ，相当于认为 | | = σ xt1）用 xt1 同除上式两侧得 ut ˆ 1 t t y x = 0 t1 x β + β1 + 2 2 1 t t x x β + 1 t t u x (5.16) 6

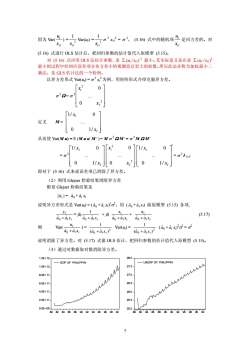
1u,。x=2，（5.16）式中的随机项兰是同方差的。对因为Var(Var(u.) =1-X1XXiX.1(5.16）式进行OLS估计后，把回归参数的估计值代入原模型（5.15)。对（5.16）式应用OLS法估计参数，求Z（ut/xa）?最小。其实际意义是在求Z（u/xl）最小的过程中给相应误差项分布方差小的观测值以更大的权数。所以此法亦称为加权最小二乘法，是GLS估计法的一个特例。以异方差形式Var(u)=α2x为例，用矩阵形式介绍克服异方差。[x0g?Q=α?..州00[1/ x定义M=01/ x从而使Var(Mu)=E(MuuM')=M。?QM=。MQM[1/ x[x?00[1/ x]0"920ITxT..x?01/xJ 001/x即对于（5.16）式来说误差项已消除了异方差。（2）利用Glejser检验结果消除异方差假设Glejser检验结果是lu,/=ao+a,x,说明异方差形式是Var(u)=（a+a,x）。用（ao+ax）除原模型（5.15）各项1x,yu,+ βi(5.17)=B-Xao+aix,ao+aixao+ajx,ao+ajx,11u,则(ao+a,x)=Var()=Var(u,)=(ao +ax,)?(ao +ajx,)2ao+ajx,说明消除了异方差。对（5.17）式做OLS估计，把回归参数的估计值代入原模型（5.15)。（3）通过对数据取对数消除异方差。1.2E+1228.0GDP OFPHIUPPINLNGDPOFPHILIPPIN27.51.0E+12AMM8.0E+1127.0 6.0E+1126.5N4.0E+11.26.0AALM2.0E+1125.50.0E+0025.08082848688909294969800028082848688909294969800027

因为 Var( 1 t t u x ) = 2 1 1 t x Var(ut) = 2 1 1 t x σ 2 xt1 2 = σ 2 ， (5.16) 式中的随机项 1 t t u x 是同方差的。对 (5.16) 式进行 OLS 估计后，把回归参数的估计值代入原模型 (5.15)。 对 (5.16) 式应用 OLS 法估计参数，求 Σ (ut / xt1) 2 最小。其实际意义是在求 Σ (ut / xt1) 2 最小的过程中给相应误差项分布方差小的观测值以更大的权数。所以此法亦称为加权最小二 乘法，是 GLS 估计法的一个特例。 以异方差形式 Var(ut) = σ 2 xt 2 为例，用矩阵形式介绍克服异方差。 σ 2 Ω = σ 2 2 1 2 0 . 0 T x x ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 定义 M = 1 1/ 0 . 0 1/ T x x ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 从而使 Var(M u) = E (M u u' M ') = M σ 2 Ω M ' = σ 2 M Ω M ' = σ 2 1 1/ 0 . 0 1/ T x x ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 2 1 2 0 . 0 T x x ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ 1 1/ 0 . 0 1/ T x x ′ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = σ 2 I T×T 即对于 (5.16) 式来说误差项已消除了异方差。 （2）利用 Glejser 检验结果消除异方差 假设 Glejser 检验结果是 | ut | = + xt ˆ 0 aˆ 1 aˆ 说明异方差形式是 Var(ut) = ( + xt) 2 σ 2 。用 ( + xt) 除原模型 (5.15) 各项, 0 aˆ 1 aˆ 0 aˆ 1 aˆ t t xaa y 10 + ˆˆ = β0 t ˆˆ 10 xaa 1 + + β1 t t xaa x 10 + ˆˆ + t t xaa u 10 + ˆˆ (5.17) 则 Var( t t xaa u 10 + ˆˆ ) = 2 10 ( ˆˆ ) 1 t + xaa Var(ut) = 2 10 ( ˆˆ ) 1 t + xaa ( + xt) 2 σ 2 = σ 2 0 aˆ 1 aˆ 说明消除了异方差。对 (5.17) 式做 OLS 估计，把回归参数的估计值代入原模型 (5.15)。 （3）通过对数据取对数消除异方差。 0.0E+00 2.0E+11 4.0E+11 6.0E+11 8.0E+11 1.0E+12 1.2E+12 80 82 84 86 88 90 92 94 96 98 00 02 GDP OF PHILIPPIN 25.0 25.5 26.0 26.5 27.0 27.5 28.0 80 82 84 86 88 90 92 94 96 98 00 02 LNGDP OF PHILIPPIN 7

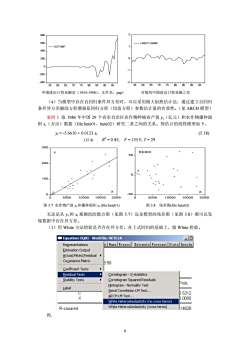
800600LNEXT-LNIMPEXT-IMP4002000.-20060657075806065707580859095558590中国进出口贸易额差（1953-1998），文件名：pap1对数的中国进出口贸易额之差（4）当模型中存在自回归条件异方差时，可以采用极大似然估计法，通过建立自回归条件异方差辅助方程增强原回归方程（均值方程）参数估计量的有效性。（见ARCH模型）案例1取1986年中国29个省市自治区农作物种植业产值y（亿元）和农作物播种面积x，（万亩）数据（file:hete01，hete02）研究二者之间的关系。得估计的线性模型如下，y=-5.6610+0.0123 xt(5.18)R2=0.85,(12.4)F=155.0,T=29300RESIDY502000-100xX50500010000150002000o50001000015000200010图5.7农作物产值y和播种面积x(file:hete01)图5.8残差图(file:hete02)无论是从y和x观测值的散点图（见图5.7）还是模型的残差图（见图5.8）都可以发现数据中存在异方差。（1）用White方法检验是否存在异方差。在上式回归的基础上，做White检验。品Equation:EQ01 Workfile:HETE1AName FreezeEstimate Forecast Stats ResidsRepresentationsEstimation OutputActual,Fitted,ResidualCoyariance MatrixB:507Coefficient TestsResidual TestsCorrelogram-Q-statisticsCorrelogram Squared ResidualsStability TestsProb.Histogram -Normality TestLabelSerial Correlation LMTest...p.5312CARCH LM Test...x0.0000White Heteroskedasticty (no cross terms)White Heteroskedasticity (cross terms)114828R-sauared得,8

-400 -200 0 200 400 600 800 55 60 65 70 75 80 85 90 95 EXT-IMP -2 -1 0 1 2 55 60 65 70 75 80 85 90 95 LNEXT-LNIMP 中国进出口贸易额差（1953-1998），文件名：pap1 对数的中国进出口贸易额之差 （4）当模型中存在自回归条件异方差时，可以采用极大似然估计法，通过建立自回归 条件异方差辅助方程增强原回归方程（均值方程）参数估计量的有效性。（见 ARCH 模型） 案例 1 取 1986 年中国 29 个省市自治区农作物种植业产值 yt（亿元）和农作物播种面 积 xt（万亩）数据（file:hete01，hete02）研究二者之间的关系。得估计的线性模型如下， yt = -5.6610 + 0.0123 xt (5.18) (12.4) R2 = 0.85, F = 155.0, T = 29 0 100 200 300 0 5000 10000 15000 20000 X Y -50 0 50 0 5000 10000 15000 20000 X RESID 图 5.7 农作物产值 yt 和播种面积 xt (file:hete01) 图 5.8 残差图(file:hete02) 无论是从 yt 和 xt 观测值的散点图（见图 5.7）还是模型的残差图（见图 5.8）都可以发 现数据中存在异方差。 （1）用 White 方法检验是否存在异方差。在上式回归的基础上，做 White 检验。 得, 8

White Heteroskedasticity Test:4.9691520.014873F-statisticProbabilityObs*R-squared8.019599Probability0.018137Test EquationDependent Variable:RESIDa2Method: Least SquaresTime:22:57Date:10/23/02Sample: 129Includedobservations:29VariableStd. ErrorProb.Coefficientt-StatisticC0.5892-219.6978401.7777-0.546814x0.1595020.1074650.14981.484227X2-3.54E-06-0.5950110.55705.95E-06注意：输出结果中的概率是指2)统计量取值大于8.02的概率为0.018。示意如下图。0.5h0.40.30.20.110因为TR2=8.02>α(2)=6，所以存在异方差。（2）用Goldfeld-Quandt方法检验是否存在异方差。①首先以x为基准对成对样本数据（y，x）按取值大小排序。②去掉中间7个数据，按x，取值大小分成样本容量各为11的两个子样本。③用两个子样本各自回归得结果如下，(5.19)y=2.7202+0.0106x，(t= 1,.., 11)R=0.80,F=33.8,SSE=1266,(5.8)y,=5.8892+0.0118 xt,(1= 19, ..., 29)(5.20)R2=0.50F=9.1,(3.0)SSE=1417414174 /(112)= 11.2,F=1266 /(11-2)因为F=11.2>Fo.05(9.9)=3.18，所以存在异方差。9

注意：输出结果中的概率是指χ 2 (2)统计量取值大于 8.02 的概率为 0.018。示意如下图。 2 4 6 8 10 0.1 0.2 0.3 0.4 0.5 因为 TR2 = 8.02 > χ 2 α (2) = 6，所以存在异方差。 （2）用 Goldfeld-Quandt 方法检验是否存在异方差。 ①首先以 xt为基准对成对样本数据（yt，xt）按取值大小排序。 ②去掉中间 7 个数据，按 xt 取值大小分成样本容量各为 11 的两个子样本。 ③用两个子样本各自回归得结果如下， yt = 2.7202 + 0.0106 xt , (t = 1, ., 11) (5.19) (5.8) R2 = 0.80, F = 33.8, SSE = 1266, yt = 5.8892 + 0.0118 xt , (t = 19, ., 29) (5.20) (3.0) R2 = 0.50, F = 9.1, SSE = 14174 F = )211/(1266 )211/(14174 − − = 11.2, 因为 F = 11.2 > F0.05 (9, 9) = 3.18，所以存在异方差。 9

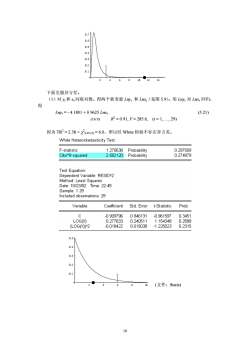
0.70.60.50.40.30.20.12104681214下面克服异方差。（1）对y,和x,同取对数。得两个新变量Lmy，和Lnx（见图5.9)。用Lny,对Lnx,回归，得(5.21)Lny,=-4.1801 +0.9625 LnxtR2=0.91, F=285.6,(t=1,,29)(16.9)因为TR2=2.58<0.05(2)=6.0，所以经White检验不存在异方差。White Heteroskedasticity Test:0.297509F-statistic1.270638Probability2.5821200.274979Obs*R-squaredProbabilityTest Equation:Dependent Variable:RESIDa2Method:Least SquaresDate:10/23/022Time:22:49Sample:129Included observations: 29VariableStd. Errort-StatisticProb.Coefficientc-0.9097960.946131-0.9615970.3451LOG()0.2776330.2405111.1543480.25890.2315(LOG()2-0.0184220.015038-1.2250230.5 0.4 0.30.20.1（文件：Statis)1084610

2 4 6 8 10 12 14 0.1 0.2 0.3 0.4 0.5 0.6 0.7 下面克服异方差。 （1）对 yt 和 xt 同取对数。得两个新变量 Lnyt 和 Lnxt （见图 5.9）。用 Lnyt 对 Lnxt 回归， 得 Lnyt = - 4.1801 + 0.9625 Lnxt . (5.21) (16.9) R2 = 0.91, F = 285.6, (t = 1, ., 29) 因为 TR2 = 2.58 < χ 2 0.05 (2) = 6.0，所以经 White 检验不存在异方差。 2 4 6 8 10 0.1 0.2 0.3 0.4 0.5 (文件：Statis) 10