《计量经济学》课程授课教案（讲稿）05 虚拟变量

虚拟变量（dummyvariable）在实际建模过程中，被解释变量不但受定量变量影响，同时还受定性变量影响。例如需要考虑性别、民族、不同历史时期、季节差异、企业所有制性质不同等因素的影响。这些因素也应该包括在模型中。由于定性变量通常表示的是某种特征的有和无，所以量化方法可采用取值为1或0。这种变量称作虚拟变量，用D表示。虚拟变量应用于模型中，对其回归系数的估计与检验方法与定量变量相同。1.截距移动设有模型，yi=β+βix+βD+ut其中y，x为定量变量；D为定性变量。当D=0或1时，上述模型可表达为，D=0β+βx, +uy,=[(B+β2)+βBx, +u,D=1D=160 YD=0404o%s20Bo+β0Bxo6020400图8.1测量截距不同D=1或0表示某种特征的有无。反映在数学上是截距不同的两个函数。若β显著不为零，说明截距不同；若β为零，说明这种分类无显著性差异。例：中国成年人体重y（kg）与身高x（cm）的回归关系如下：D=1(男)-105+xy=-100+x-5D=-100+xD=0(女)注意：①若定性变量含有m个类别，应引入m-1个虚拟变量，否则会导致多重共线性，称作虚拟变量陷阱（dummyvariabletrap）。②关于定性变量中的哪个类别取0，哪个类别取1，是任意的，不影响检验结果。定性变量中取值为0所对应的类别称作基础类别（basecategory）。④对于多于两个类别的定性变量可采用设一个虚拟变量而对不同类别采取赋值不同的方法处理。如：(大学)1D=0(中学)-1(小学)。1

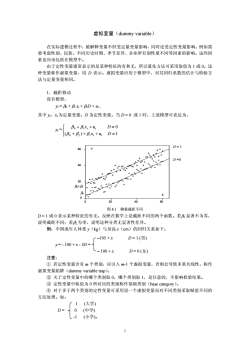
虚拟变量（dummy variable） 在实际建模过程中，被解释变量不但受定量变量影响，同时还受定性变量影响。例如需 要考虑性别、民族、不同历史时期、季节差异、企业所有制性质不同等因素的影响。这些因 素也应该包括在模型中。 由于定性变量通常表示的是某种特征的有和无，所以量化方法可采用取值为 1 或 0。这 种变量称作虚拟变量，用 D 表示。虚拟变量应用于模型中，对其回归系数的估计与检验方 法与定量变量相同。 1．截距移动 设有模型， yt = β0 + β1 xt + β2D + ut , 其中 yt，xt 为定量变量；D 为定性变量。当 D = 0 或 1 时，上述模型可表达为， yt = ⎩ ⎨ ⎧ =+++ ++ = )( 1 0 120 10 Dux Dux tt tt βββ ββ 0 20 40 60 0 20 40 60 X Y D = 1 D =0 β0+β2 β0 图 8.1 测量截距不同 D = 1 或 0 表示某种特征的有无。反映在数学上是截距不同的两个函数。若β2 显著不为零， 说明截距不同；若β2 为零，说明这种分类无显著性差异。 例：中国成年人体重 y（kg）与身高 x（cm）的回归关系如下： –105 + x D = 1 (男) y = - 100 + x - 5D = – 100 + x D = 0 (女) 注意： ① 若定性变量含有 m 个类别，应引入 m-1 个虚拟变量，否则会导致多重共线性，称作 虚拟变量陷阱（dummy variable trap）。 ② 关于定性变量中的哪个类别取 0，哪个类别取 1，是任意的，不影响检验结果。 ③ 定性变量中取值为 0 所对应的类别称作基础类别（base category）。 ④ 对于多于两个类别的定性变量可采用设一个虚拟变量而对不同类别采取赋值不同的 方法处理。如： 1 (大学) D = 0 (中学) -1 (小学)。 1

例1：市场用煤销售量模型（file:Dummy1）我国市场用煤销量的季节性数据（1982-1988，《中国统计年鉴》1987，1989）见下图与表。由于受取暖用煤的影响，每年第四季度的销售量大大高于其它季度。鉴于是季节数据可设三个季节变量如下：1（4季度）1(3季度）（2季度）D, =D, =D, =0（1,2,3季度）0（1,2,4季度）L0（1,3,4季度）55005500-Y2731.03+57.15T50005000 450045004000400035003000250025008848788887788B85全国按季节市场用煤销售量数据（file:Dummy1）季度Y,D,D2D3季度Y,DiD2D311000150101982.12599.811985.33159.121982.22647.2001985.44483.216100130.001982.32912.70101986.12881.8171982.44087.041001986.23308.71800150001983.12806.5001986.33437.5191001983.22672.16011986.44946.8201070001983.32943.6001987.13209.021-I1983.44193.481001987.23608.1220011984.13001.99001987.33815.623010001984.22969.5100011987.45332.324101984.3113929.8250003287.50101988.11984.44270.612101988.24126.226001013000270101985.13044.11988.34015.12801985.23078.8140011988.44904.210数据来源：《中国统计年鉴》1989。注：以季节数据D,为例，EViews命令是DI=@seas(4)。以时间t为解释变量（1982年1季度取1=1）的煤销售量（y）模型如下：y=2431.20 + 49.00 1+1388.09 D,+ 201.84D+85.00D3(1)(26.04)(10.81)(13.43)(1.96)(0.83)R= 0.95, DW = 1.2, s.e.= 191.7, F=100.4, 7=28, t0.05 (28-5)= 2.07由于D2，D，的系数没有显著性，说明第2，3季度可以归并入基础类别第1季度。于是只考虑加入一个虚拟变量D，把季节因素分为第四季度和第一、二、三季度两类。从上式中剔除虚拟变量D2，D3，得煤销售量（y）模型如下：(2)y= 2515.86 + 49.73 1+1290.91 D,(32.03(10.63)(14.79)R = 0.94, DW = 1.4, s.e. = 198.7, F = 184.9, 7=28, t0.05(25)= 2.06进一步检验斜率是否有变化，在上式中加入变量1D，y= 2509.07 + 50.22 t+1321.19 D,- 1.95 tD(3) (28.24)(9.13)(6.85)(-0.17)2

例 1：市场用煤销售量模型（file: Dummy1） 我国市场用煤销量的季节性数据（1982-1988，《中国统计年鉴》1987，1989）见下图与 表。由于受取暖用煤的影响，每年第四季度的销售量大大高于其它季度。鉴于是季节数据可 设三个季节变量如下： 1 （4 季度） 1 （3 季度） 1 （2 季度） D1 = D2 = D3 = 0 （1, 2, 3 季度） 0 （1, 2, 4 季度） 0 （1, 3, 4 季度） 2500 3000 3500 4000 4500 5000 5500 82 83 84 85 86 87 88 Y 2500 3000 3500 4000 4500 5000 5500 82 83 84 85 86 87 88 Y 2731.03+57.15*T 全国按季节市场用煤销售量数据（file: Dummy1） 季度 Yt t D1 D2 D3 季度 Yt t D1 D2 D3 1982.1 2599.8 1 0 0 0 1985.3 3159.1 15 0 1 0 1982.2 2647.2 2 0 0 1 1985.4 4483.2 16 1 0 0 1982.3 2912.7 3 0 1 0 1986.1 2881.8 17 0 0 0 1982.4 4087.0 4 1 0 0 1986.2 3308.7 18 0 0 1 1983.1 2806.5 5 0 0 0 1986.3 3437.5 19 0 1 0 1983.2 2672.1 6 0 0 1 1986.4 4946.8 20 1 0 0 1983.3 2943.6 7 0 1 0 1987.1 3209.0 21 0 0 0 1983.4 4193.4 8 1 0 0 1987.2 3608.1 22 0 0 1 1984.1 3001.9 9 0 0 0 1987.3 3815.6 23 0 1 0 1984.2 2969.5 10 0 0 1 1987.4 5332.3 24 1 0 0 1984.3 3287.5 11 0 1 0 1988.1 3929.8 25 0 0 0 1984.4 4270.6 12 1 0 0 1988.2 4126.2 26 0 0 1 1985.1 3044.1 13 0 0 0 1988.3 4015.1 27 0 1 0 1985.2 3078.8 14 0 0 1 1988.4 4904.2 28 1 0 0 数据来源：《中国统计年鉴》1989。注：以季节数据 D1 为例，EViews 命令是 D1= @seas(4)。 以时间 t 为解释变量（1982 年 1 季度取 t = 1）的煤销售量（y）模型如下： y = 2431.20 + 49.00 t + 1388.09 D1 + 201.84 D2 + 85.00 D3 (1) (26.04) (10.81) (13.43) (1.96) (0.83) R2 = 0.95, DW = 1.2, s.e. = 191.7, F=100.4, T=28, t0.05 (28-5) = 2.07 由于 D2，D3的系数没有显著性，说明第 2，3 季度可以归并入基础类别第 1 季度。于是只考 虑加入一个虚拟变量 D1，把季节因素分为第四季度和第一、二、三季度两类。从上式中剔 除虚拟变量 D2，D3，得煤销售量（y）模型如下： y = 2515.86 + 49.73 t + 1290.91 D1 (2) (32.03 (10.63) (14.79) R2 = 0.94, DW = 1.4, s.e. = 198.7, F = 184.9, T=28, t0.05 (25) = 2.06 进一步检验斜率是否有变化，在上式中加入变量 t D1， y = 2509.07 + 50.22 t + 1321.19 D1 - 1.95 t D1 (3) (28.24) (9.13) (6.85) (-0.17) 2

R =0.94, DW= 1.4, s.e. = 202.8, F= 118.5, T=28, t0.05 (24)= 2.06由于回归系数-1.95所对应的1值是-0.17，可见斜率未发生变化。因此以模型（2）作为最后确立的模型。若不采用虚拟变量，得回归结果如下，y=2731.03+57.15t(4)(4.0)(11.6)R = 0.38, DW=2.5, s.e. = 608.8, T = 28, t0.05 (26)= 2.06与（2）式相比，回归式（4）显得很差。2.斜率变化以上只考虑定性变量影响截距，未考虑影响斜率，即回归系数的变化。当需要考虑时，可建立如下模型：y=β+x,+D+βxD+ut,其中x为定量变量：D为定性变量。当D=0或1时，上述模型可表达为，D=0β。 +β,x, +utyi=D=1[(β。+β,)+(β +β,)x, +u,通过检验β是否为零，可判断模型斜率是否发生变化。10070YYA6080111AAA504460401444444943040eo2020100000TX00上20402040060060图8.5情形1（不同类别数据的截距和斜率不同）图8.6情形2（不同类别数据的截距和斜率不同）例2：用虚拟变量区别不同历史时期（file:dummy2）中国进出口贸易总额数据（1950-1984）见上表。试检验改革前后该时间序列的斜率是否发生变化。定义虚拟变量D如下(1950-1977)0D=(1978-1984)3

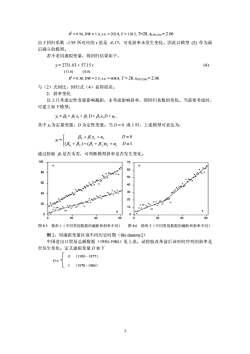
R2 = 0.94, DW = 1.4, s.e. = 202.8, F = 118.5, T=28, t0.05 (24) = 2.06 由于回归系数 -1.95 所对应的 t 值是 -0.17，可见斜率未发生变化。因此以模型 (2) 作为最 后确立的模型。 若不采用虚拟变量，得回归结果如下， y = 2731.03 + 57.15 t (4) (11.6) (4.0) R2 = 0.38, DW = 2.5, s.e. = 608.8, T = 28, t0.05 (26) = 2.06 与（2）式相比，回归式（4）显得很差。 2．斜率变化 以上只考虑定性变量影响截距，未考虑影响斜率，即回归系数的变化。当需要考虑时， 可建立如下模型： yt = β0 + β1 xt + β2 D + β3 xt D + ut , 其中 xt 为定量变量；D 为定性变量。当 D = 0 或 1 时，上述模型可表达为， yt = ⎩ ⎨ ⎧ =++++ ++ = )()( 1 0 20 31 10 Dux ux D tt tt ββββ ββ 通过检验 β3是否为零，可判断模型斜率是否发生变化。 0 20 40 60 80 100 0 20 40 60 X Y 0 10 20 30 40 50 60 70 0 20 40 60 T Y 图 8.5 情形 1（不同类别数据的截距和斜率不同） 图 8.6 情形 2（不同类别数据的截距和斜率不同） 例 2：用虚拟变量区别不同历史时期（file:dummy2） 中国进出口贸易总额数据（1950-1984）见上表。试检验改革前后该时间序列的斜率是 否发生变化。定义虚拟变量 D 如下 0 （1950 - 1977） D = 1 （1978 - 1984） 3

14+TRADE121096421950195519601965197019751980中国进出口贸易总额数据（1950-1984）（单位：百亿元人民币）年DDtradetimetimeD年tradetimetimeD19500.41510019681.085190019510.595200196920001.069000019520.646319701.12921000019530.809419711.209225001972230019540.8471.46919551.09860019732.205240010019561.087019742.923250800260019571.04519752.90419589002.64127001.287197619591.493100019772.7252800196011003.550291291.284197812003019610.90819794.546130133119620.8090019805.63831119630.857140019817.3533213219640.975150019827.7133313313419651.184160019838.60134035-3519661.271170198412.0100019671.12218以时间time为解释变量，进出口贸易总额用trade表示，估计结果如下：trade=0.37+0.066time-33.96D+1.20timeD(1.86)(5.53)(-10.98)(12.42)0.37+0.066time(D= 0, 1950 - 1977)33.59+1.27time(D=1, 1978 - 1984)上式说明，改革前后无论截距和斜率都发生了变化。进出口贸易总额的年平均增长量扩大了18倍。例3：香港季节GDP数据（单位：千亿港元）的拟合（虚拟变量应用，file:dummy6）3.63.6→ GDP+GDPAn3213212N2.828N2.424N2.020N31.6-N1.612+290919293949596979899000102909192939495969798990001021990~1997年香港季度GDP呈线性增长。1997年由于遭受东南亚金融危机的影响，经4

中国进出口贸易总额数据（1950-1984） （单位：百亿元人民币） 年 trade time D time D 年 trade time D time D 1950 0.415 1 0 0 1968 1.085 19 0 0 1951 0.595 2 0 0 1969 1.069 20 0 0 1952 0.646 3 0 0 1970 1.129 21 0 0 1953 0.809 4 0 0 1971 1.209 22 0 0 1954 0.847 5 0 0 1972 1.469 23 0 0 1955 1.098 6 0 0 1973 2.205 24 0 0 1956 1.087 7 0 0 1974 2.923 25 0 0 1957 1.045 8 0 0 1975 2.904 26 0 0 1958 1.287 9 0 0 1976 2.641 27 0 0 1959 1.493 10 0 0 1977 2.725 28 0 0 1960 1.284 11 0 0 1978 3.550 29 1 29 1961 0.908 12 0 0 1979 4.546 30 1 30 1962 0.809 13 0 0 1980 5.638 31 1 31 1963 0.857 14 0 0 1981 7.353 32 1 32 1964 0.975 15 0 0 1982 7.713 33 1 33 1965 1.184 16 0 0 1983 8.601 34 1 34 1966 1.271 17 0 0 1984 12.010 35 1 35 1967 1.122 18 0 0 以时间 time 为解释变量，进出口贸易总额用 trade 表示，估计结果如下： trade = 0.37 + 0.066 time - 33.96D + 1.20 time D (1.86) (5.53) (-10.98) (12.42) 0.37 + 0.066 time (D = 0, 1950 - 1977) = - 33.59 + 1.27 time (D = 1, 1978 - 1984) 上式说明，改革前后无论截距和斜率都发生了变化。进出口贸易总额的年平均增长量扩大了 18 倍。 例 3：香港季节 GDP 数据（单位：千亿港元）的拟合（虚拟变量应用, file:dummy6） 1.2 1.6 2.0 2.4 2.8 3.2 3.6 90 91 92 93 94 95 96 97 98 99 00 01 02 GDP 1990~1997 年香港季度 GDP 呈线性增长。1997 年由于遭受东南亚金融危机的影响，经 4

济发展处于停滞状态，1998~2002年底GDP总量几乎没有增长（见上图）。对这样一种先增长后停滞，且含有季节性周期变化的过程简单地用一条直线去拟合显然是不恰当的。为区别不同季节，和不同时期，定义季节虚拟变量D2、D3、D4和区别不同时期的虚拟变量DT如下（数据见附录）：I2（第2季度）D2 =人0(其他季度)1（第3季度）D3=0（其他季度）1（第4季度）D4 0（其他季度）（1998:1~2002:4)1DT =LO(1990:1~1997:4)得估计结果如下：GDP,=1.1573+0.06681+0.0775D2+0.2098D;+0.2349D+1.8338DT-0.0654DTxt(3.7)(9.9)(11.0)(19.9)(50.8)(64.6)(-28.0)R = 0.99, DW = 0.9, s.e. =0.05, F=1198.4, T=52, t0.05 (52-7)= 2.01对于1990:1~1997:4GDP,=1.1573+ 0.0668 1+ 0.0775 D,+ 0.2098 D,+ 0.2349 D对于1998:1~2002:4GDP,=2.9911+0.0014t+0.0775D2+0.2098D;+0.2349D4Dependent Variable:GDPMethod: Least SquaresDate:04/04/04Time:15:54Sample: 1990:1 2002:4Included observations:52VariableCoefficientStd. Errort-StatisticProb.OT1.1573000.02277850.808140.00000.00000.0668430.00103564.56095D20.0775220.0211393.6673250.0006D30.2098290.0212159.8907990.0000D40.2349220.02134111.008270.0000DT1.8337860.09207919.915260.0000DT*T0.0023330.0000-0.065419-28.039512.695174R-squared0.993780Mean dependent varAdjusted R-squared0.992951S.D. dependent var0.6411440.053829S.E. of regressionAkaike info criterion-2.8813760.130388Sum squared residSchwarz criterion-2.61870881.91576F-statistic1198.382Log likelihoodDurbin-Watson stat0.910754Prob(F-statistic)0.0000005

济发展处于停滞状态，1998~2002 年底 GDP 总量几乎没有增长（见上图）。对这样一种先增 长后停滞，且含有季节性周期变化的过程简单地用一条直线去拟合显然是不恰当的。为区别 不同季节，和不同时期，定义季节虚拟变量 D2、D3、D4 和区别不同时期的虚拟变量 DT 如下（数据见附录）： 1 （第 2 季度） D2 = 0 （其他季度） 1 （第 3 季度） D3 = 0 （其他季度） 1 （第 4 季度） D4 = 0 （其他季度） 1 （1998:1~2002:4） DT = 0 （1990:1 ~1997:4） 得估计结果如下： GDPt = 1.1573 + 0.0668 t + 0.0775 D2 + 0.2098 D3 + 0.2349 D4+ 1.8338 DT - 0.0654 DT× t (50.8) (64.6) (3.7) (9.9) (11.0) (19.9) (-28.0) R2 = 0.99, DW = 0.9, s.e. = 0.05, F=1198.4, T=52, t0.05 (52-7) = 2.01 对于 1990:1 ~1997:4 GDPt = 1.1573 + 0.0668 t + 0.0775 D2 + 0.2098 D3 + 0.2349 D4 对于 1998:1~2002:4 GDPt = 2.9911 + 0.0014 t + 0.0775 D2 + 0.2098 D3 + 0.2349 D4 5

如果不采用虚拟变量拟合效果将很差。GDP,=1.6952 +0.0377 t(20.6)(13.9)R2= 0.80, DW= 0.3, T=52, t0.05(52-2)= 2.01案例5天津市粮食市场小麦批发价与面粉零售价的关系研究（file:xiezhiyong）首先看天津市粮食市场小麦批发价格的变化情况（图1）。1995年初，天津市粮食市场的小麦批发价格首先放开。在经历5个月的上扬之后，进入平稳波动期。从1996年8月份开始小麦批发价格一路走低。至2002年12月份，小麦批发价格降至是1160元/吨。其次看面粉零售价的变化情况。因为面粉零售价格直接关系到居民的日常生活，所以开始时没有与小麦批发价格一起放开。当小麦批发价格一路看涨时，1995年1月至1996年6月面粉零售价格一直处于2.14元于克的水平上。1996年7月起，面粉零售价格也开始在市场上放开。受小麦批发价格上涨的影响，一个月内面粉零售价格从2.14元/千克涨到2.74元/于克。在这个价位上坚持了11个月之后，面粉零售价格开始下降。与小麦批发价格的下降相一致，在经历了5年零7个月的变化之后，面粉零售价格又恢复到接近开放前2.14元/千克的水平上（2.17元）。散点图如图2。按时间分析这些观测点的变化情况（见图3，逆时针方向运动）。见图4，直接拟合这些数据效果将很差（R2=0.027,r=0.17)。co2.8wholesaleretail price.18002.616002.8140026.2.4,12002.4.10002.2-..2.2wholesale2.0.2.09698990001029597100012001400180016002000图1图22.82.8retail priceretailprice2.6.2.6.2.42.4.2.22.2".wholesalewholesale2.02.0140018001200160010001200160020001000140018002000图3图4利用虚拟变量技术，在模型中加入虚拟变量。定义D=0，（1995:1~1996:6，面粉零售价格放开之前），D=1，（1996:7~2002：12，面粉零售价格放开之后）取对数关系建立模型。Lnsale的系数没有显著性（对于面粉零售价格放开之前的散点来说回归直线是一条水平线）。剔出Lnsale变量，得估计结果6

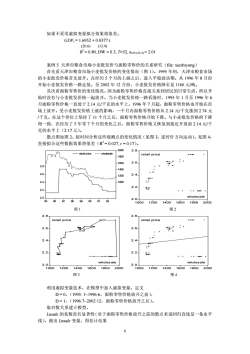
如果不采用虚拟变量拟合效果将很差。 GDPt = 1.6952 + 0.0377 t (20.6) (13.9) R2 = 0.80, DW = 0.3, T=52, t0.05 (52-2) = 2.01 案例 5 天津市粮食市场小麦批发价与面粉零售价的关系研究（file: xiezhiyong） 首先看天津市粮食市场小麦批发价格的变化情况（图 1）。1995 年初，天津市粮食市场 的小麦批发价格首先放开。在经历 5 个月的上扬之后，进入平稳波动期。从 1996 年 8 月份 开始小麦批发价格一路走低。至 2002 年 12 月份，小麦批发价格降至是 1160 元/吨。 其次看面粉零售价的变化情况。因为面粉零售价格直接关系到居民的日常生活，所以开 始时没有与小麦批发价格一起放开。当小麦批发价格一路看涨时，1995 年 1 月至 1996 年 6 月面粉零售价格一直处于 2.14 元/千克的水平上。1996 年 7 月起，面粉零售价格也开始在市 场上放开。受小麦批发价格上涨的影响，一个月内面粉零售价格从 2.14 元/千克涨到 2.74 元 /千克。在这个价位上坚持了 11 个月之后，面粉零售价格开始下降。与小麦批发价格的下降 相一致，在经历了 5 年零 7 个月的变化之后，面粉零售价格又恢复到接近开放前 2.14 元/千 克的水平上（2.17 元）。 散点图如图 2。按时间分析这些观测点的变化情况（见图 3，逆时针方向运动）。见图 4， 直接拟合这些数据效果将很差（R2 = 0.027, r = 0.17）。 2.0 2.2 2.4 2.6 2.8 1000 1200 1400 1600 1800 2000 95 96 97 98 99 00 01 02 retail price wholesale 2.0 2.2 2.4 2.6 2.8 1000 1200 1400 1600 1800 2000 wholesale retail price 图 1 图 2 2.0 2.2 2.4 2.6 2.8 1000 1200 1400 1600 1800 2000 wholesale retail price 2.0 2.2 2.4 2.6 2.8 1000 1200 1400 1600 1800 2000 wholesale retail price 图 3 图 4 利用虚拟变量技术，在模型中加入虚拟变量。定义 D = 0，（1995: 1~1996:6，面粉零售价格放开之前）， D = 1，（1996:7~2002:12，面粉零售价格放开之后）。 取对数关系建立模型。 Lnsale 的系数没有显著性（对于面粉零售价格放开之前的散点来说回归直线是一条水平 线）。剔出 Lnsale 变量，得估计结果 6

PRICE=2.140+1.1215 LnsalexD-7.7458×DR2= 0.9054,(131.5)(23.9)(-23.0)D=0PRICE =2.140,PRICE=-5.6058+1.1215Lnsale,D=1一条回归直线的斜率为零，一条回归直线的斜率为为1.12。可决系数从不加虚拟变量模型的0.046增加到0.905（输出结果见下）。DependentVariable:PRICEMethod: Least SquaresDate:03/07/04Time:22:02Sample:1995:012002:12Included observations:96VariableCoefficientStd. Errort-StatisticProb.C0.33802.1400002.2217340.9632120.295461-5.87E-121.0000LOG(SALE)-1.73E-12D1-7.7458482.247429-3.4465370.0009LOG(SALE)*D11.1214670.2991913.7483310.0003R-squared0.9054122.401115Mean dependent var0.9023280.222056Adjusted R-squaredS.D. dependent varS.E. of regression0.069398Akaike info criterion-2.457132Sum squared resid0.443085Schwarz criterion-2.350285Log likelihood121.9424F-statistic293.54630.000000Durbin-Watson stat0.300302Prob(F-statistic)DependentVariable:PRICEMethod: Least SquaresDate:03/21/044Time:22:51Sample:1995:012002:12Included observations:96VariableCoefficientStd, ErrorProb.t-Statisticc2.1400000.016269131.53710.0000D1-7.745848-22.954450.00000.337444LOG(SALE)*D11.1214670.04684323.941090.0000R-squared0.9054122.401115Mean dependent var0.903378S.D. dependent var0.222056Adjusted R-squaredS.E. of regression0.069024-2.477966Akaike info criterion0.443085Sum squared residSchwarz criterion-2.397830121.9424445.1055Log likelihoodF-statistic0.300302Prob(F-statistic)0.000000Durbin-Watson stat本例也可以建立倒数模型：7

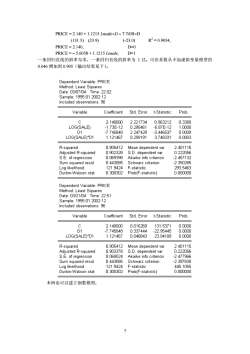
PRICE = 2.140 + 1.1215 Lnsale×D – 7.7458×D (131.5) (23.9) (-23.0) R2 = 0.9054, PRICE = 2.140, D=0 PRICE = – 5.6058 + 1.1215 Lnsale, D=1 一条回归直线的斜率为零，一条回归直线的斜率为 1.12。可决系数从不加虚拟变量模型的 0.046 增加到 0.905（输出结果见下）。 本例也可以建立倒数模型： 7

2.8PRICE..2.62.4:2.2.1/SALE2.0+0.00040.00050.00060.00070.00080.00090.001Dependent Variable:PRICEMethod:LeastSquaresDate: 03/23/04Time:08:08Sample:1995:012002:12Included observations: 96VariableCoefficientStd. Errort-StatisticProb.c0.00002.1400000.014669145.8851D11.5141340.04715232.111960.0000(1/SALE)*D1-1565.936-26.952450.000058.09996R-squared0.9231032.401115Mean dependent varAdjusted R-squared0.921449S.D. dependent var0.222056S.E.of regression0.062236Akaike info criterion-2.685027Sumsquaredresid0.360215-2.604891Schwarz criterion131.8813558.2030Log likelihoodF-statistic0.333294Prob(F-statistic)0.000000Durbin-Watson statPRICE=2.140+1.5141xD-1565.9(1/sale)xDR2= 0.9231,(32.1)(-27.0)(145.9) D=0PRICE = 2.140,D=1PRICE = 3.6541 1565.9 (1/sale),8

2.0 2.2 2.4 2.6 2.8 0.00040.00050.00060.00070.00080.00090.001 1/SALE PRICE PRICE = 2.140 + 1.5141×D – 1565.9 (1/sale) ×D (145.9) (32.1) (-27.0) R2 = 0.9231, PRICE = 2.140, D=0 PRICE = 3.6541 – 1565.9 (1/sale), D=1 8