《计量经济学》课程授课教案（讲稿）11 时间序列模型

2.3自相关函数以上介绍了随机过程的几种模型。实际中单凭对时间序列的观察很难确定其属于哪一种模型，而自相关函数和偏自相关函数是分析随机过程和识别模型的有力工具。1.自相关函数定义在给出自相关函数定义之前先介绍自协方差函数概念。由第一节知随机过程x中的每一个元素x，1=1,2，…都是随机变量。对于平稳的随机过程，其期望为常数，用μ表示，即(2.25)E(x)=μ, t=1,2, ..随机过程的取值将以μ为中心上下变动。平稳随机过程的方差也是一个常量Var(x) =E [(xr- E(x)]=E [(xr- μ)°]= o?, 1= 1, 2, ..(2.26)2用来度量随机过程取值对其均值的离散程度。相隔k期的两个随机变量x与xt-的协方差即滞后k期的自协方差，定义为(2.27)= Cov (xi, X1-)=E[(x -μ) (Xr--μ))自协方差序列，k=0,1,..K称为随机过程x的自协方差函数。当k=0时20 = Var (x) = 0.2自相关系数定义Cov(X,Xf-x)(2.28)Pk=Var(x,) /Var(x-)因为对于一个平稳过程有Var (x) = Var (xt- ) = α?(2.29)所以（2.28）可以改写为P=Cor- -4= (2.30)o0.2Yo当k=0时，有eo=1。以滞后期k为变量的自相关系数列(2.31)Pk,k=0,1,...,K称为自相关函数。因为pk=p.k即Cov(xt-k，x）=Cov(xx+k），自相关函数是零对称的，所以实际研究中只给出自相关函数的正半部分即可。2.自回归过程的自相关函数(1）平稳AR(1)过程的自相关函数AR(1)过程如下x,=x-+u，<1已知E(x)=0。用xi-k同乘上式两侧X,X-A= OX-IX-A+u,X-k上式两侧同取期望，1

2.3 自相关函数 以上介绍了随机过程的几种模型。实际中单凭对时间序列的观察很难确定其属于哪一种 模型，而自相关函数和偏自相关函数是分析随机过程和识别模型的有力工具。 1. 自相关函数定义 在给出自相关函数定义之前先介绍自协方差函数概念。由第一节知随机过程{xt}中的每 一个元素 xt，t = 1, 2, . 都是随机变量。对于平稳的随机过程，其期望为常数，用 μ 表示， 即 E(x t) = μ, t = 1, 2, . (2.25) 随机过程的取值将以 μ 为中心上下变动。平稳随机过程的方差也是一个常量 Var(xt) = E [(xt - E(xt))2 ] = E [(xt - μ) 2 ] = σx 2 , t = 1, 2, . (2.26) σx 2 用来度量随机过程取值对其均值 μ 的离散程度。 相隔 k 期的两个随机变量 xt 与 xt - k 的协方差即滞后 k 期的自协方差，定义为 γk = Cov (xt, x t - k ) = E[(xt - μ ) (xt - k - μ ) ] (2.27) 自协方差序列 γk , k = 0, 1, ., K, 称为随机过程 {xt} 的自协方差函数。当 k = 0 时 γ0 = Var (xt) = σx 2 自相关系数定义 ρk = )()( ),( t kt ktt xVarxarV xxCov − − （2.28） 因为对于一个平稳过程有 Var (xt) = Var (xt - k) = σx 2 (2.29) 所以（2.28）可以改写为 ρk = 2 ),( x ktt xxCov σ − = 2 x k σ γ = 0 γ γ k （2.30） 当 k = 0 时，有 ρ 0 = 1。 以滞后期 k 为变量的自相关系数列 ρk, k = 0, 1, ., K (2.31) 称为自相关函数。因为ρk = ρ- k 即 Cov (xt - k , xt ) = Cov (xt, xt + k )，自相关函数是零对称的， 所以实际研究中只给出自相关函数的正半部分即可。 2.自回归过程的自相关函数 (1) 平稳 AR(1)过程的自相关函数 AR(1) 过程如下 xt = φ1 xt-1 + ut , |φ1| < 1 已知 E(xt) = 0。用 xt- k 同乘上式两侧 xt xt- k = φ1 xt-1 xt- k + ut xt- k 上式两侧同取期望， 1

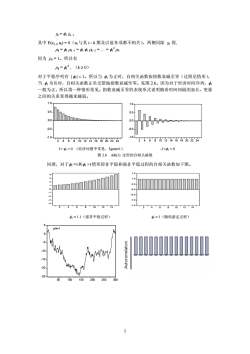
=K-1其中E(xtu)=0（u,与其t-k期及以前各项都不相关)。两侧同除%得，Pk=0Pk-1=010Pk-2=...=0po因为p%=1。所以有Pk=*，(k≥0)对于平稳序列有|>0（经济问题中常见，5gener1）-1<<0图2.6AR(I)过程的自相关函数同理，对于=1和1情形即非平稳和强非平稳过程的自相关函数如下图。=1.1（强非平稳过程）=1（随机游走过程）phi=1e-10--15MM-20.252500150200n

γk = φ1 γk -1 其中 E(xt- k ut) = 0（ut 与其 t - k 期及以前各项都不相关）。两侧同除 γ0 得, ρk = φ1 ρk -1 = φ1 φ1 ρk -2 = . = φ1 k ρ0 因为 ρo = 1。所以有 ρk = φ1 k , （k ≥ 0） 对于平稳序列有 | φ1| φ1 > 0 （经济问题中常见，5gener1） -11情形即非平稳和强非平稳过程的自相关函数如下图。 -4 -3 -2 -1 0 1 2 3 4 2 4 6 8 10 12 14 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5 2 4 6 8 10 12 14 φ1 = 1.1（强非平稳过程） φ1 = 1（随机游走过程） -25 -20 -15 -10 -5 0 5 50 100 150 200 250 300 phi=1 2

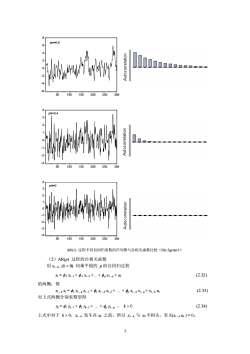
phi=0.8ao15050100200250300phi=0.43.50100150200250300100150200*250300AR(1）过程不同自回归系数的序列图与自相关函数比较（file:5gener1)）（2）AR(p）过程的自相关函数用xt-k，（k>0）同乘平稳的p阶自回归过程(2.32)X,=01x-1+02Xi-2+..+0pX-p+u的两侧，得(2.33)X,-x,=orXf-Xf-1+ Xf-kx-2+...+opXf-kx-p+x,-ku对上式两侧分别求期望得=k-I+k-2+..+k-p，k>0(2.34)上式中对于k>0，xt-发生在ut之前，所以xt-与u不相关，有E(xi-u)=0。3

-6 -4 -2 0 2 4 6 8 50 100 150 200 250 300 phi=0.8 -3 -2 -1 0 1 2 3 4 50 100 150 200 250 300 phi=0.4 -4 -3 -2 -1 0 1 2 3 4 50 100 150 200 250 300 phi=0 AR(1) 过程不同自回归系数的序列图与自相关函数比较（file:5gener1） （2）AR(p) 过程的自相关函数 用 xt - k , (k > 0) 同乘平稳的 p 阶自回归过程 xt = φ 1 xt -1 + φ 2 xt -2 +.+ φ p xt - p + ut (2.32) 的两侧，得 xt - k xt = φ1 xt - k xt -1 + φ2 xt - k xt -2 + . + φp xt - k xt - p + xt - k ut (2.33) 对上式两侧分别求期望得 γk = φ1 γk -1 + φ2 γk -2 + . + φp γk - p ， k > 0 (2.34) 上式中对于 k > 0，xt - k 发生在 ut 之前，所以 xt - k 与 ut 不相关，有 E(xt - k ut ) = 0。 3

用%分别除（2.34）式的两侧得Yule-Walker方程Pe=Pk-1+Pk-2+...+pPkp，>0(2.35)令L)=(1-L--.-LP）其中L为k的滞后算子，则上式可表达为d(L) pr= 0因d(L)可因式分解为，α(L)=II(1-G,L),i=l则（2.35）式的通解（证明见附录，不要求掌握）是Pk=A1G*+ A2G2*+.. + ApGk(2.36)其中Aii=1...为待定常数。这里Gi",i=1,2,,P是特征方程L)=(1--L-...-P)=0的根。为保证随机过程的平稳性，要求IGl<1,i=1,2.…,P。这会遇到如下两种情形。①当G，为实数时，（2.36）式中的A,G*将随着k的增加而几何衰减至零，称为指数衰减（过阻尼情形）。小虚轴T38实轴a②当G,和G,表示一对共轭复数根时，设G,=α+bi,G=a-bi，则G和G,的极座标形b式分别表示为G,=Reio和G,=Re-i0，其中R=Va?+b2表示G,和G,的模，Q=arctga、b分别表示该共轭复数根的实部与虚部。则A,G+A,G表示为AGK+AG(23)由于G,和G,是共轭复数，所以，尽管A，A是任意数，但必须是共轭复数以保证p(h)是实数。令A=Be'，A=Be-，其中B表示A和A的模，Φ=arctg，d、c分别表示该共轭复数根的实部与虚部。于是有，AG+AG=Be'9 Rkeiko + Be-iΦ Rke-iko=BRk(ei(ka+) +e-i(ko+0))由三角公式eia+e-iα=2cosα，上式得，AG+AG*=BR*(e(k0+0) +e-(k0+0)=2BR* cos(k0+0)其中B，是任意实数。是初相角，用弧度表示。4

用 γ0 分别除（2.34）式的两侧得 Yule-Walker 方程 ρk = φ1 ρk -1 + φ2 ρk -2 + . + φp ρk -p ， k > 0 (2.35) 令 Φ(L) = (1 - φ1 L - φ2 L2 - . - φp Lp ）其中 L 为 k 的滞后算子，则上式可表达为 Φ(L) ρk = 0 因 Φ(L) 可因式分解为， Φ(L) =∏ , = p i iLG 1 ) -(1 则（2.35）式的通解（证明见附录，不要求掌握）是 ρk = A1 G1 k + A2 G2 k + . + Ap Gp k . (2.36) 其中 Ai, i = 1, . p 为待定常数。这里 Gi -1, i = 1, 2, ., p 是特征方程 Φ(L) = (1 - φ1 L - φ2 L2 - . - φp Lp ) = 0 的根。为保证随机过程的平稳性，要求 | Gi | < 1, i = 1, 2, ., p。这会遇到如下两种情形。 ① 当 Gi为实数时，(2.36) 式中的 Ai Gi k 将随着 k 的增加而几何衰减至零，称为指数衰 减（过阻尼情形）。 ②当 Gi和 Gj表示一对共轭复数根时，设 Gi = a + bi, Gj= a – bi，则 Gi 和 Gj的极座标形 式分别表示为 和 ，其中 R= iθ i = eRG iθ j eRG − = 22 + ba 表示 Gi 和 Gj 的模， ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = a b θ arctg ， a、b 分别表示该共轭复数根的实部与虚部。则 Ai Gi k + Aj Gjk 表示为 A Gi k + A Gjk （23） 由于 Gi 和 Gj 是共轭复数，所以，尽管 A， A 是任意数，但必须是共轭复数以保证ρk (h) 是实数。令 ，iφ = BeA iφ BeA − = ，其中 B 表示 A 和 A 的模， ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = d c φ arctg ，d、c 分别表示 该共轭复数根的实部与虚部。于是有， A Gi k + A Gjk = = ikki ikki θφθφ eRBeeRBe −− + ( ) φθ +−+ φθ )()( + kik ki eeBR 由三角公式 ee −ii αα =+ cos2 α ，上式得， A Gi k + A Gjk = ( ) = φθ +−+ φθ )()( + kik ki eeBR kBR +φθ )cos(2 k 其中 B，φ是任意实数。φ是初相角，用弧度表示。 4

对于平稳过程，由于模R1时， =E [(u,+ ur-1)(ut-+ ut-k-I)]=0综合以上三种情形，MA(1)过程自相关函数为5

对于平稳过程，由于模 R 1 时， γk = E [(ut + θ1 ut -1) (ut – k + θ1 ut – k -1)] = 0 综合以上三种情形，MA(1)过程自相关函数为 5

0k=11+02YkPr=YoOk>1见图2.7。1.01.00.50.50.0 0.0-0.50.5-1.0.1.0-2468101214161820222424681012141618202224>001时，P=0。(2)MA(g)）过程的自相关函数MA(g）过程的自相关函数是0k+010k+1+020k+2+...+0q-k0gk=12...Pr=1+02+02+..+0?0,k>q当k>q时，P=0，说明Pk，k=0,1,.具有截尾特征。例如，对于MA(2）过程，自相关函数是020,+0,02PI=Pr=0,k>2Py=1+0,2 +0,31+0,2 +0,3（注意：模型移动平均项的符号以及这里Pk的符号正好与Box-Jenkins书中的符号相反，这样表示的好处是保持与计算机输出结果一致。）4.ARMA(1,1）过程的自相关函数0--(+00x6+0) - (+00)6 +0)（证明略）01+02+26( +) +(1)=E(X-kx)=E(X-R(0X-1 +ur +01u-l)=1k-1Pe=x/%=1Y-1/%=ΦPk=1"p=单,个1（1+0+），≥2( +)+(1)ARMA（1，1）过程的自相关函数pk从Pr开始指数衰减。pi的大小取决于和I，pi的符号取决于（+）。若>0，（+0，自相关函数是正的、平滑的指数衰减，若>0，（+<0，自相关函数是负的、平滑的指数衰减。若<0，自相关函数为正负交替式指数衰减，当（+のi）为正数时，k为奇数时，自相关系数为正：k为偶数时，自相关系数为负。当（+の）为负时，k为奇数时，自相关系数为负；k为偶数时，自相关系数为正。5.对于ARMA(p,9）过程，P,q≥2时，自相关函数是指数衰减或正弦衰减的。6.相关图（correlogram，或估计的自相关函数，样本自相关函数）对于一个有限时间序列（x1,x2，.，x）用样本平均数6

ρk = 0 γ γ k = 1 2 1 , 1 1 0, 1 k k θ θ ⎧ = ⎪ + ⎨ ⎪ ⎩ > 见图 2.7。 -1.0 -0.5 0.0 0.5 1.0 2 4 6 8 10 12 14 16 18 20 22 24 -1.0 -0.5 0.0 0.5 1.0 2 4 6 8 10 12 14 16 18 20 22 24 θ1 > 0 θ1 1 时，ρk = 0。 (2) MA(q) 过程的自相关函数 MA(q) 过程的自相关函数是 ρk = ⎪ ⎩ ⎪ ⎨ ⎧ > = ++++ + + ++++ − qk qk q kk k qkq ,0 ,.2,1, 1 . . 2 2 2 2 1 2211 θθθ θθθθθ θθ 当 k > q 时，ρk = 0，说明 ρk , k = 0, 1, . 具有截尾特征。 例如，对于 MA(2) 过程，自相关函数是 ρ1= 2 2 2 1 211 1 θθ θ θ θ ++ + , ρ2= 2 2 2 1 2 1 θθ θ ++ , ρk = 0, k > 2。 （注意：模型移动平均项的符号以及这里 ρk的符号正好与 Box-Jenkins 书中的符号相反， 这样表示的好处是保持与计算机输出结果一致。） 4. ARMA (1, 1) 过程的自相关函数 )1()( ))(1( 21 ))(1( 2 1 2 11 1111 11 2 1 1111 0 1 1 φφθ θφφθ φθθ θφφθ γ γ ρ −++ ++ = ++ ++ == (证明略) γk = E(xt-k xt) = E(xt-k (φ 1 xt-1+ ut +θ 1 ut-1)) = φ 1γk-1 ρk=γk /γ0 =φ 1γk-1/γ0 = φ 1ρk-1= φ 1 k-1 ρ1= φ 1 k-1 )1()( ))(1( 2 2 1111 φφθ θφφθ −++ ++ 11 1 , k ≥2 ARMA (1, 1) 过程的自相关函数ρk 从 ρ1 开始指数衰减。ρ1 的大小取决于 φ1 和 θ1, ρ1 的符号取决于 (φ1 +θ1 )。若 φ1 > 0，(φ1 +θ1 )> 0，自相关函数是正的、平滑的指数衰减，若 φ1 > 0，(φ1 +θ1 )< 0，自相关函数是负的、平滑的指数衰减。若 φ1 < 0，自相关函数为正负交替 式指数衰减，当(φ1 +θ1 )为正数时，k 为奇数时，自相关系数为正；k 为偶数时，自相关系数 为负。当(φ1 +θ1 )为负时，k 为奇数时，自相关系数为负；k 为偶数时，自相关系数为正。 5．对于 ARMA (p, q) 过程，p, q ≥ 2 时，自相关函数是指数衰减或正弦衰减的。 6. 相关图（correlogram，或估计的自相关函数，样本自相关函数） 对于一个有限时间序列（x1, x2, ., xT）用样本平均数 6

->x7(=l估计总体均值μ，用样本方差17?=Z(x, -x)2T Lt=l估计总体方差。定义估计的自协方差-(2.42)Ck=7kk=0, 1,2,...,K,=(=11a-DCo=Y0=(2.43)T是时间序列数据的样本容量。实际中T不应太小，最好能大于60。则当用样本矩估计随机过程的自相关函数，Ckk=0.1.2.....K(K<T)rk=Co称其为相关图或估计的自相关函数。rk是对p的估计。注意：（2.42)式分母为T，不是T-k。C为有偏估计量。但在小样本条件下更有效。相关图是对自相关函数的估计。由于MA过程和ARMA过程中的MA分量的自相关函数具有截尾特性，所以通过相关图可以估计MA过程的阶数9。相关图是识别MA过程阶数和ARMA过程中MA分量阶数的一个重要方法。对于年度时间序列数据，相关图一般取k=15就足够了。r的方差近似为T。所以在观察相关图时，若r的绝对值超过2T12（2个标准差），就被认为是显著地不为零。当T充分大时，近似有(k-0) / T12 =r 7/2 _ N (0, 1)2.4偏自相关函数偏自相关函数是描述随机过程结构特征的另一种方法。用邮表示k阶自回归式中第个回归系数，则k阶自回归模型表示为X,= O1X-I + Ok2X1-2 +...+0X-k +u其中是最后一个回归系数。若把k=1,2...的一系列回归式看作是滞后期k的函数，则称Ouk, k=1,2...(2.45)为偏自相关函数。它由下式中的红项组成。X=X-I +uX,= 021 Xf-1 + 022 X-2 + u,.X,= Ok1X-1 + Ok2X12 +... +pxXr-k +u,因偏自相关函数中每一个回归系数u恰好表示x,与x-在排除了其中间变量x-1x-2xk+影响之后的相关系数，7

x = T 1 ∑= T t t x 1 估计总体均值 μ，用样本方差 s 2 = 2 1 )( 1 ∑= − T t t xx T 估计总体方差σx 2 。 定义估计的自协方差 ∑ − = == + −− kT t kk ktt xxxx T C 1 ),)(( 1 γˆ k = 0, 1, 2, ., K , (2.42) C0 = 0 γˆ = 2 1 )( 1 ∑= − T t t xx T (2.43) T 是时间序列数据的样本容量。实际中 T 不应太小，最好能大于 60。 则当用样本矩估计随机过程的自相关函数， rk = C0 Ck , k = 0, 1 , 2, ., K, ( K < T ) 称其为相关图或估计的自相关函数。rk 是对ρk的估计。 注意：(2.42)式分母为 T，不是 T-k。Ck为有偏估计量。但在小样本条件下更有效。 相关图是对自相关函数的估计。由于 MA 过程和 ARMA 过程中的 MA 分量的自相关函 数具有截尾特性，所以通过相关图可以估计 MA 过程的阶数 q。相关图是识别 MA 过程阶数 和 ARMA 过程中 MA 分量阶数的一个重要方法。对于年度时间序列数据，相关图一般取 k = 15 就足够了。 rk的方差近似为 T-1。所以在观察相关图时，若 rk的绝对值超过 2 T-1/2（2 个标准差）， 就被认为是显著地不为零。当 T 充分大时，近似有 (rk -0) / T-1/2 = rk T1/2 ~ N (0, 1) 2.4 偏自相关函数 偏自相关函数是描述随机过程结构特征的另一种方法。用 φkj 表示 k 阶自回归式中第 j 个回归系数，则 k 阶自回归模型表示为 xt = φk 1 xt-1 + φk 2 xt-2 + . + φkk xt-k + ut 其中 φkk 是最后一个回归系数。若把 k = 1, 2.的一系列回归式φkk看作是滞后期 k 的函数， 则称 φkk, k = 1, 2 . (2.45) 为偏自相关函数。它由下式中的红项组成。 xt = φ11 xt-1 + ut xt = φ21 xt-1 + φ22 xt-2 + ut . xt = φk 1 xt-1 + φk 2 xt-2 + . + φkk xt-k + ut 因偏自相关函数中每一个回归系数φkk 恰好表示 xt 与 xt-k在排除了其中间变量 xt-1,xt-2,.,xt-k +1 影响之后的相关系数， 7

X,-1x-1-02x2--..-1x-k+1=0x-+u所以偏自相关函数由此得名。用Φk，表达（2.35）式，Yule-Walker方程，得(2.46)P,=Φip-+Φk2pi-2+... +Φkkpj-k, j=1,2,..,K用矩阵形式表示上式，[pi]1P1P2gk!Pk-1P2P1P1”Pk-29k2(2.47)...-1LPkLokkLPk-1Pk-2Pk-3或p=Pe则s=p"p,将k=1,2，…代入上式连续求解，可求得偏自相关函数Φ=pl,-piTPI-PiP21Pi1-P1P2-Pr01P221-1P21-022P2P01 p/21pi其中P2-p?Φ22=1-p?对于AR(1)过程，x,=1x-I+u，当k=1时，±0：当k>1时，=0。所以AR(1)过程的偏自相关函数特征是在k=1出现峰值（m=pi）然后截尾。1.01.00.5.0.50.0 0.0-0.50.51.02468101214161820222424681012141618202224>0u2时，账=0。偏自相关函数在滞后期2以后有截尾特性。对于AR(p)过程，当k≤p时，0：当k>p时，=0。偏自相关函数在滞后期p以后有截尾特性，因此可用此特征识别AR(p)过程的阶数。8

xt - φk 1 xt-1 - φk 2 xt-2 - . - φkk-1 xt-k +1 = φkk xt-k + ut 所以偏自相关函数由此得名。 用 φ k j 表达（2.35）式，Yule-Walker 方程,得 ρj = φ k 1 ρj -1 + φ k 2 ρj - 2 + . + φ k k ρj - k , j = 1, 2, ., K . (2.46) 用矩阵形式表示上式， = (2.47) ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ρ k ρ ρ . 2 1 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ −−− − − 1. . 1 . 1 . 321 1 1 2 21 1 kkk k k ρρρ ρ ρρ ρρρ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ kk k k φ φ φ . 2 1 或 ρ = P φ. 则 φ = P -1 ρ, 将 k = 1, 2 , . 代入上式连续求解，可求得偏自相关函数 φ 11 = ρ1, ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 22 21 φ φ = = 1 1 1 1 1 − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ρ ρ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 2 1 ρ ρ 1 1 1 1 1 1 2 1 1 1 ρ ρ ρ ρ ρ ρ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − = 2 1 2 12 211 1 ρ ρρ ρρρ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − 其中 φ 22 = 2 1 2 12 1 ρ ρρ − − . 对于 AR(1)过程，xt = φ11 xt-1 + ut，当 k = 1 时，φ11 ≠ 0；当 k > 1 时，φkk = 0。所以 AR(1) 过程的偏自相关函数特征是在 k = 1 出现峰值（φ11 = ρ1）然后截尾。 -1.0 -0.5 0.0 0.5 1.0 2 4 6 8 10 12 14 16 18 20 22 24 -1.0 -0.5 0.0 0.5 1.0 2 4 6 8 10 12 14 16 18 20 22 24 φ11 > 0 φ11 2 时，φkk = 0。偏自相关函数在滞后期 2 以 后有截尾特性。 对于 AR(p)过程，当 k ≤ p 时，φkk ≠ 0；当 k > p 时，φkk = 0。偏自相关函数在滞后期 p 以后有截尾特性，因此可用此特征识别 AR(p)过程的阶数。 8

对于MA(1)过程x=u+u-1，有[1/(1+のL)]x,=ut，(1- L+ 0L? -... )x,= ut,X=01x-1 -0x-2+0xi3-.+ut,当6>0时，自回归系数的符号是正负交替的；当600,<0MA(1）过程的偏自相关函数对于MA(2）过程，若?(L)=0的根是实数，偏自相关函数由两个指数衰减形式叠加而成。若?(L)=0的根是复数，偏自相关函数呈正弦衰减形式。因为任何一个可逆的MA(g）过程都可以转换成一个无限阶的系数按几何递减的AR过程，所以MA(g）过程的偏自相关函数呈缓慢衰减特征。ARMA(p,q）过程的偏自相关函数也是无限延长的，其表现形式与MA(q)过程的偏自相关函数相类似。根据模型中移动平均部分的阶数9以及参数6,的不同，偏自相关函数呈指数衰减和（或）正弦衰减混合形式。对于时间序列数据，偏自相关函数通常是未知的。可以用样本计算11，22，.的估计量1，2。估计的偏自相关函数Φk, k=1,2,..,K,(2.48)称为偏相关图。因为AR过程和ARMA过程中AR分量的偏自相关函数具有截尾特性，所以可利用偏相关图估计自回归过程的阶数p。实际中对于偏相关图取k=15就足可以了。更以的方差近似为T。当T充分大时，近似有(- 0) / T12= TI2~N(0, 1)所以在观察偏相关图时，若的绝对值超过2T12（2个标准差），就被认为是显著地不为零。9

对于 MA(1)过程 xt = ut + θ1 ut-1，有 [1/ (1+ θ1 L)] xt = ut ， (1- θ1 L + θ1 2 L2 - . ) xt = ut , xt = θ1 x t-1 - θ1 2 x t-2 +θ1 3 x t-3 -. + ut , 当θ1 > 0 时，自回归系数的符号是正负交替的；当θ1 0 θ1 < 0 MA(1) 过程的偏自相关函数 对于 MA(2) 过程，若Θ (L) = 0 的根是实数，偏自相关函数由两个指数衰减形式叠加而 成。若Θ (L) = 0 的根是复数，偏自相关函数呈正弦衰减形式。 因为任何一个可逆的 MA(q) 过程都可以转换成一个无限阶的系数按几何递减的 AR 过 程，所以 MA(q) 过程的偏自相关函数呈缓慢衰减特征。 ARMA( p, q) 过程的偏自相关函数也是无限延长的，其表现形式与 MA(q)过程的偏自相 关函数相类似。根据模型中移动平均部分的阶数 q 以及参数θi的不同，偏自相关函数呈指数 衰减和（或）正弦衰减混合形式。 对于时间序列数据，偏自相关函数通常是未知的。可以用样本计算 φ11, φ22, . 的估计 量 φ ˆ 11 , , . φ ˆ 22 。估计的偏自相关函数 , k = 1, 2, ., K, (2.48) φ kk ˆ 称为偏相关图。因为 AR 过程和 ARMA 过程中 AR 分量的偏自相关函数具有截尾特性，所 以可利用偏相关图估计自回归过程的阶数 p。实际中对于偏相关图取 k = 15 就足可以了。 φ kk ˆ 的方差近似为 T-1。当 T 充分大时，近似有 ( - 0) / T-1/2 = T1/2 ~ N (0, 1) φ kk ˆ φ kk ˆ 所以在观察偏相关图时，若 的绝对值超过 2 T-1/2（2 个标准差），就被认为是显著地不为 零。 φ kk ˆ 9

Date:09/29/07Time:14:51Sample:1949 1998Includedobservations:49ACPACQ-StatPartial CorrelationProbAutocorrelation0.60318.906110.6030.00011I120.237-0.19721.9050.000口！30.1210.11222.7020.00021-40.064-0.04522.9310.00015-0.011-0.05222.9380.000/D6 -0.072 -0.04623.2370.00117-0.151-0.12624.5970.0018-0.1610.00526.1760.001I0I-9-0.186 -0.12728.3320.001Id-10-0.215-0.06431.2980.001注：2个标准差=2T-12=2（1/7）=0.286。图中虚线表示到中心线2个标准差宽度。用EViews计算估计的自相关函数和偏自相关函数。点击View选correlogram功能。2.5时间序列模型的建立与预测一，识别用相关图和偏相关图识别模型形式（确定参数dp,q）-估计4.对初步选取的模型进行参数估计+三、诊断与检验包括参数的显著性检验和残差的随机性检验+不可取模型可取吗可取止图2.8建立时间序列模型程序图ARIMA过程y用(L) (4sy)= α0(L) u(2.51)表示，其中@(L)和(L)分别是p,q阶的以L为变数的多项式，它们的根都在单位圆之外。α为4"y,过程的漂移项，y表示对y进行d次差分之后可以表达为一个平稳的可逆的ARMA过程。这是随机过程的一般表达式。它既包括了AR，MA和ARMA过程，也包括了单整的AR，MA和ARMA过程。10

注：2 个标准差 = 2 T -1/2 = 2（1/7）= 0.286。图中虚线表示到中心线 2 个标准差宽度。 用 EViews 计算估计的自相关函数和偏自相关函数。点击 View 选 correlogram 功能。 2.5 时间序列模型的建立与预测 一．识别 用相关图和偏相关图识别模型 形式（确定参数 d, p, q） 二．估计 对初步选取的模型进行参数估计 三．诊断与检验 包括参数的显著性检验和 残差的随机性检验 模型可取吗 不可取 可取 止 图 2.8 建立时间序列模型程序图 ARIMA 过程 yt 用 Φ (L) ( Δd yt) = α+Θ (L) ut (2.51) 表示，其中Φ (L)和Θ (L)分别是 p, q 阶的以 L 为变数的多项式，它们的根都在单位圆之外。 α为Δd yt过程的漂移项，Δd yt表示对yt 进行d次差分之后可以表达为一个平稳的可逆的ARMA 过程。这是随机过程的一般表达式。它既包括了 AR，MA 和 ARMA 过程，也包括了单整 的 AR，MA 和 ARMA 过程。 10