《计量经济学》课程教学资源（实验指导）实验五 自相关性

实验五自相关性【实验目的】掌握自相关性的检验与处理方法。【实验内容】利用表3-1资料，试建立建立美国的生产函数模型，并检验模型的自相关性。【实验步骤】、回归模型的估计按照前面的结果，C-D生产函数的估计式为：Iny=-3.9377+1.4508lnL+0.3838lnKt=(-16.6149)(17.4314)(7.9930)R2=0.9943F=3332.181R2=0.9946二、自相关性检验1.DW检验；因为n=39，k=1，取显著性水平α=0.05时，查表得d，=1.382，du=1.597，而0<0.8581=DW<d，，所以存在（正）自相关。2.偏相关系数检验在方程窗口中点击View/ResidualTest/Correlogram-Q-statistics，并输入滞后期为10，则会得到残差e,与e-1,e,-2,e-1o的各期相关系数和偏相关系数，如图5-1所示。Equation:EQoiTorkfile: UNIIILED::Untitledt回风View ProcObject Print Name FreezeEstimateForecast stats ResidsCorrelogram of ResidualsDate:08/11/11Time:23:57Sample:19291967Includedobservations:39ACPACQ-StatProbAutocorrelationPartial Correlation0.0000.5590.55913.145122-0.046-0.52213.2380.0011IC3-0.1930.27514.9000.0020.1260.005国4.0.05515.03750.201-0.09316.9370.005160.047-0.07317.0460.00917-0.204-0.12319.1220.008一8-0.325-0.18424.5690.002I0.0019-0.2060.04426.822I10-0.158-0.36628.2020.002

实验五 自相关性 【实验目的】 掌握自相关性的检验与处理方法。 【实验内容】 利用表 3-1 资料，试建立建立美国的生产函数模型，并检验模型的自相关性。 【实验步骤】 一、回归模型的估计 按照前面的结果，C-D 生产函数的估计式为： ln 3.9377 1.4508ln 0.3838ln y L K ˆ = − + + t ＝(-16.6149) (17.4314) (7.9930) 2 R = 0.9946 2 R = 0.9943 F = 3332.181 二、自相关性检验 ⒈DW 检验； 因为 n＝39，k＝1，取显著性水平  ＝0.05 时，查表得 L d ＝1.382， U d ＝1.597，而 0<0.8581＝DW< L d ，所以存在（正）自相关。 ⒉偏相关系数检验 在方程窗口中点击 View/Residual Test/Correlogram-Q-statistics，并输入滞后期为 10，则会得到残差 t e 与 1 2 10 , , t− t− t− e e e 的各期相关系数和偏相关系数，如图 5-1 所示

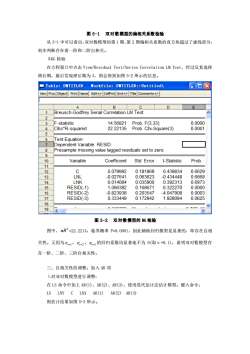
图5-1双对数模型的偏相关系数检验从5-1中可以看出，双对数模型的第1期、第2期偏相关系数的直方块超过了虚线部分，初步判断存在着一阶和二阶自相关。3.BG检验在方程窗口中点击View/ResidualTest/SeriesCorrelationLMTest，经过反复选择滞后期，最后发现滞后期为3，则会得到如图5-2所示的信息。Table:UHIILEDForkfile: UNIIILED::Untitledy口回区ViewProcobject PrintNameEdit+/-CellFmtGrid+/-Title Comments+/-ABCDEABreusch-GodfreySerialCorrelationLMTest:2F-statistic14.56821Prob.F(3,33)0.0000222.221350.00014Obs*R-squaredProb.Chi-Square(3)56TestEquationDependentVariable:RESID78Presamplemissingvaluelaggedresiduals settozero.910VariableCoefficientStd.Errort-StatisticProb.11C0.6629120.0799920.1818690.439834LNL0.666813-0.0276410.063623-0.434448LNK140.0140840.0359000.3923130.6973RESID(-1)0.0000151.0663820.1686716.32227016RESID(-2)-0.8239380.203547-4.0479080.0003170.0625RESID(-3)0.3334490.1729421.92809418110FA-.19C7图5-2双对数模型的BG检验图中，nR2=22.2214，临界概率P=0.0001，因此辅助回归模型是显著的，即存在自相关性。又因为et-1et-2”ei-3的回归系数均显著地不为0(取a=0.1)，说明双对数模型存在一阶、二阶、三阶自相关性。三、自相关性的调整：加入AR项1.对双对数模型进行调整；在LS命令中加上AR1)、AR(2)、AR(3)，使用送代估计法估计模型。键入命令：LSLNYCLNXAR(1)AR(2)AR(3)则估计结果如图5-3所示

图 5-1 双对数模型的偏相关系数检验 从 5-1 中可以看出，双对数模型的第 1 期、第 2 期偏相关系数的直方块超过了虚线部分， 初步判断存在着一阶和二阶自相关。 ⒊BG 检验 在方程窗口中点击 View/Residual Test/Series Correlation LM Test，经过反复选择 滞后期，最后发现滞后期为 3，则会得到如图 5-2 所示的信息。 图 5-2 双对数模型的 BG 检验 图中， 2 nR =22.2214，临界概率 P=0.0001，因此辅助回归模型是显著的，即存在自相 关性。又因为 t−1 e ， t−2 e ， t 3 e − 的回归系数均显著地不为 0(取α=0.1)，说明双对数模型存 在一阶、二阶、三阶自相关性。 三、自相关性的调整：加入 AR 项 ⒈对双对数模型进行调整； 在 LS 命令中加上 AR(1)、AR(2)、AR(3)，使用迭代估计法估计模型。键入命令： LS LNY C LNX AR(1) AR(2) AR(3) 则估计结果如图 5-3 所示

Iable:UNIIILEDForkfile: UHIIILED::Untitledy口回区ViewProcObjectPrintNameEdit+/-CellFmtGrid+/-Title Comments+/-BCDEADependentVariable:LNYA2Convergenceachievedafter12iterations34VariableCoefficientStd.Errort-StatisticProb.5C6-2.5199220.513896-4.9035670.00007LNL0.1311030.00001.0425307.951990LNK80.5468440.0842026.4944360.000090.0000AR(1)1.3549820.1766087.67226610AR(2)-0.9205320.240179-3.8326950.0006AR(3)0.0179110.3992220.1593552.5052401213R-squared0.997990Meandependentvar5.7318590.9976560.45152814AdjustedR-squaredS.D.dependentvar15S.E.ofregression0.021863Akaike info criterion-4.65703816Sumsquaredresid0.014340Schwarz criterion-4.3931181789.82668-4.564923Log likelihoodHannan-Quinncriter18F-statistic2979.7361.866548Durbin-Watson statAAAAA19<>图5-3加入AR项的双对数模型估计结果图5-3表明，估计过程经过12次选代后收敛；PI、P,和P,的估计值分别为1.3550、-0.9205和0.3992，并且1检验显著，说明双对数模型确实存在一阶、二阶、三阶自相关性。调整后模型的DW=1.8665，n=36，k=2，取显著性水平α=0.05时，查表得d，=1.354，du=1.587，而du<1.8665=DW<4一du，说明模型不存在一阶自相关性。因此，美国的C-D生产函数模型为：Inj=-2.5199+1.0425ln/+0.5468lnk+et=(7.9520)(6.4944)=1.3550g--0.92536,2+0.3992T=(7.6723)(-3.8327)(2.5052)

图 5-3 加入 AR 项的双对数模型估计结果 图 5-3 表明，估计过程经过 12 次迭代后收敛； 1、 2 和 3 的估计值分别为 1.3550、 -0.9205 和 0.3992，并且 t 检验显著，说明双对数模型确实存在一阶、二阶、三阶自相关性。 调整后模型的 DW＝1.8665，n＝36，k＝2，取显著性水平  ＝0.05 时，查表得 L d ＝1.354， Ud ＝1.587，而 Ud <1.8665＝DW<4－ Ud ，说明模型不存在一阶自相关性。因此，美国的 C-D 生产函数模型为： ln 2.5199 1.0425ln 0.5468ln y l k ˆ = − + + +ε t = (7.9520) (6.4944) 1 2 1.3550 0.9253 0.3992 t t    = − + − − T= (7.6723) (-3.8327) (2.5052)