《计量经济学》课程授课教案（讲稿）07 自相关

自相关1：非自相关假定由第2节知回归模型的假定条件之一是，Cov(ui,u)=E(uu)=0, (i,jeT, ij),(1.1)即误差项u的取值在时间上是相互无关的。称误差项u非自相关。如果Cov(ui,u)±0, (i+j)则称误差项u存在自相关。自相关又称序列相关。原指一随机变量在时间上与其滞后项之间的相关。这里主要是指回归模型中随机误差项u与其滞后项的相关关系。自相关也是相关关系的一种。2.一阶自相关自相关按形式可分为两类。(1）一阶自回归形式当误差项u只与其滞后一期值有关时，即u,=f(ut-)+V称u具有一阶自回归形式。(2）高阶自回归形式当误差项u的本期值不仅与其前一期值有关，而且与其前若干期的值都有关系时，即u=f(ut-1, u(-2,..)+v则称u具有高阶自回归形式。通常假定误差项的自相关是线性的。因计量经济模型中自相关的最常见形式是一阶自回归形式，所以下面重点讨论误差项的线性一阶自回归形式，即(1.2)=-+V其中α是自回归系数，V是随机误差项。满足通常假设E(v)=0, 1=1,2...,TVar(v)=o2, I=1,2.., T,Cov(vi, y)=0, i+j, i,j=1,2.., T,Cov(ux-1, v)=0, 1=1, 2 ..., T,依据普通最小二乘法公式，模型（1.2）中αi的估计公式是，(p-Z--(,-2)1e2a,=(1.3)E(x, -)2Zu.21=2其中T是样本容量。若把ut,ut-看作两个变量，则它们的相关系数是Z, ( -(x, -)Q：(1.4)(r(1- /(4 -x)Vuu1=21=2(1.5)对于大样本显然有Z u,u,-1=2(=21

自相关 1. 非自相关假定 由第 2 节知回归模型的假定条件之一是， Cov(ui, uj ) = E(ui uj) = 0, (i, j ∈ T, i ≠ j), (1.1) 即误差项 ut的取值在时间上是相互无关的。称误差项 ut 非自相关。如果 Cov (ui , uj ) ≠ 0, (i ≠ j) 则称误差项 ut 存在自相关。 自相关又称序列相关。原指一随机变量在时间上与其滞后项之间的相关。这里主要是指 回归模型中随机误差项 ut 与其滞后项的相关关系。自相关也是相关关系的一种。 2．一阶自相关 自相关按形式可分为两类。 (1) 一阶自回归形式 当误差项 ut只与其滞后一期值有关时，即 ut = f (ut - 1) + vt 称 ut 具有一阶自回归形式。 (2) 高阶自回归形式 当误差项 ut的本期值不仅与其前一期值有关，而且与其前若干期的值都有关系时，即 ut = f (ut – 1, u t – 2 , . ) + vt 则称 ut 具有高阶自回归形式。 通常假定误差项的自相关是线性的。因计量经济模型中自相关的最常见形式是一阶自回 归形式，所以下面重点讨论误差项的线性一阶自回归形式，即 ut = α1 ut -1 + vt (1.2) 其中α1 是自回归系数，vt 是随机误差项。vt 满足通常假设 E(vt) = 0, t = 1, 2 ., T, Var(vt) = σv 2 , t = 1, 2 ., T, Cov(vi, vj ) = 0, i ≠ j, i, j = 1, 2 ., T, Cov(ut-1, vt) = 0, t = 1, 2 ., T, 依据普通最小二乘法公式，模型（1.2）中 α1 的估计公式是， = 1 aˆ ∑ ∑ = − = − T t t T t tt u uu 2 2 1 2 1 ( 1= ˆ β ∑ ∑ − −− 2 )( ))(( xx xxyy t tt ) (1.3) 其中 T 是样本容量。若把 ut, u t-1 看作两个变量，则它们的相关系数是 ρˆ = ∑∑ ∑ = − = = − T t t T t t T t tt uu uu 2 2 1 2 2 2 1 (r = ∑∑ ∑ = = = − − −− T t t T t t T t tt yy xx xxyy 1 2 1 2 1 )()( ))(( ) (1.4) 对于大样本显然有 ∑ ≈ (1.5) = T t ut 2 2 ∑= − T t ut 2 2 1 1

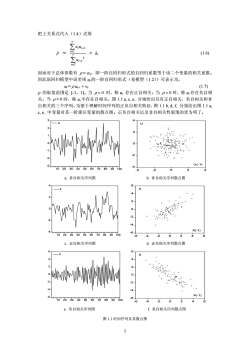
把上关系式代入（1.4）式得t=2X(1.6)a2Eu(=2因而对于总体参数有β=αi，即一阶自回归形式的自回归系数等于该二个变量的相关系数。因此原回归模型中误差项u的一阶自回归形式（见模型（1.2)）可表示为，(1.7)u=pu-i+vr.p的取值范围是[-1，1]。当p>0时，称u,存在正自相关；当p<0时，称u,存在负自相关。当p=0时，称u不存在自相关。图1.1a.c,e，分别给出具有正自相关，负自相关和非自相关的三个序列。为便于理解时间序列的正负自相关特征，图1.1b.d.f分别给出图1.1ac,e，中变量对其一阶滞后变量的散点图。正负自相关以及非自相关性展现的更为明了。U(-1)102030405060708090100-202a非自相关序列图b.非自相关序列散点图X4.20-24X(-1)102030405060708090100A-2024c.正自相关序列图d.正自相关序列散点图RA2.0.-2-X(-1).602030405060708090100-2406e.负自相关序列图f.负自相关序列散点图图1.1时间序列及其散点图2

把上关系式代入（1.4）式得 ρˆ ≈ ∑ ∑ = − = − T t t T t tt u uu 2 2 1 2 1 = (1.6) 1 aˆ 因而对于总体参数有 ρ = α1，即一阶自回归形式的自回归系数等于该二个变量的相关系数。 因此原回归模型中误差项 ut 的一阶自回归形式（见模型（1.2））可表示为， ut = ρ ut-1 + vt. (1.7) ρ 的取值范围是 [-1，1]。当 ρ > 0 时，称 ut 存在正自相关；当 ρ < 0 时，称 ut 存在负自相 关。当 ρ = 0 时，称 ut 不存在自相关。图 1.1 a, c, e, 分别给出具有正自相关，负自相关和非 自相关的三个序列。为便于理解时间序列的正负自相关特征，图 1.1 b, d, f, 分别给出图 1.1 a, c, e, 中变量对其一阶滞后变量的散点图。正负自相关以及非自相关性展现的更为明了。 -3 -2 -1 0 1 2 3 10 20 30 40 50 60 70 80 90 100 U -4 -2 0 2 4 -4 -2 0 2 4 U(-1) U a. 非自相关序列图 b. 非自相关序列散点图 -4 -2 0 2 4 10 20 30 40 50 60 70 80 90 100 X -6 -4 -2 0 2 4 6 -6 -4 -2 0 2 4 6 X(-1) X c. 正自相关序列图 d. 正自相关序列散点图 -6 -4 -2 0 2 4 6 10 20 30 40 50 60 70 80 90 100 X -6 -4 -2 0 2 4 6 -6 -4 -2 0 2 4 6 X(-1) X e. 负自相关序列图 f. 负自相关序列散点图 图 1.1 时间序列及其散点图 2

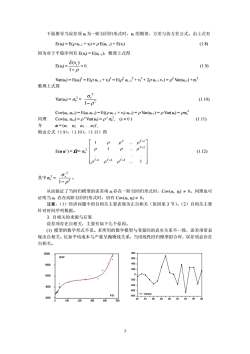
下面推导当误差项u为一阶自回归形式时，u的期望、方差与协方差公式。由上式有(1.8)E(u)=E(put-+v)=pE(ur-)+E(v)因为对于平稳序列有 E(u)=E(u-1)，整理上式得E()=0.(1.9)E(u):1-pVar(u)=E(u) =E(p ut-1 + y)"=E(p ut-} + v? + 2p ut-1 v)= Var(ut-1) +o,整理上式得Var(u) = 0, = 0, (1.10)1-p2Cov(ui, ut-1)= E(ut ui-1) = E(p ut-1 + v) ur-1) = p Var(ut-1)= p Var(u)= po,同理Cov(u, ut-s)= p"Var(u)=p"or2,(1.11)(s±0)令=(2...r),则由公式（1.9），（1.10），（1.11）得D207-11p1ppE(uu')=Q=02(1.12)C其中20从而验证了当回归模型的误差项u存在一阶自回归形式时，Cov(ui，u）0。同理也可证明当ut存在高阶自回归形式时，仍有Cov(ui,u）+0。注意，（1）经济问题中的自相关主要表现为正自相关（原因见3节）。（2）自相关主要针对时间序列数据。3.自相关的来源与后果误差项存在自相关，主要有如下几个原因。（1）模型的数学形式不妥。若所用的数学模型与变量间的真实关系不一致，误差项常表现出自相关。比如平均成本与产量呈抛物线关系，当用线性回归模型拟合时，误差项必存在自相关。8001000GDP600400800020060c02004004000600RESIDFDI80n2000828486&o925001002303004003

下面推导当误差项 ut 为一阶自回归形式时，ut 的期望、方差与协方差公式。由上式有 E(ut) = E(ρ ut -1 + vt) = ρ E(ut -1) + E(vt) (1.8) 因为对于平稳序列有 E(ut) = E(ut -1)，整理上式得 E(ut) = ( ) 1 E vt − ρ = 0. (1.9) Var(ut) = E(ut) 2 = E(ρ ut -1 + vt) 2 = E(ρ 2 ut –1 2 + vt 2 + 2ρ ut -1 vt ) = ρ 2 Var(ut-1) +σv 2 整理上式得 Var(ut) = σu 2 = 2 2 1 σ v − ρ (1.10) Cov(ut, ut-1) = E(ut ut-1) = E((ρ ut -1 + vt) ut-1) = ρ Var(ut-1) = ρ Var(ut) = ρσu 2 同理 Cov(ut, ut-s) = ρs Var(ut) = ρs σu 2 , (s ≠ 0 ) (1.11) 令 u = (u1 u2 u3 . uT)’, 则由公式（1.9），（1.10），（1.11）得 E(u u’ ) = Ω = σu 2 (1.12) ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ −− − − − 1. . 1 . 1 . 321 2 2 1 TT T T T ρρρ ρ ρρ ρρρ 其中σu 2 = 2 2 1 σ v − ρ 。 从而验证了当回归模型的误差项 ut存在一阶自回归形式时，Cov(ui, uj) ≠ 0。同理也可 证明当 ut 存在高阶自回归形式时，仍有 Cov(ui, uj) ≠ 0。 注意，（1）经济问题中的自相关主要表现为正自相关（原因见 3 节）。（2）自相关主要 针对时间序列数据。 3. 自相关的来源与后果 误差项存在自相关，主要有如下几个原因。 (1) 模型的数学形式不妥。若所用的数学模型与变量间的真实关系不一致，误差项常表 现出自相关。比如平均成本与产量呈抛物线关系，当用线性回归模型拟合时，误差项必存在 自相关。 -800 -600 -400 -200 0 200 400 600 800 82 84 86 88 90 92 94 96 98 RESID 3

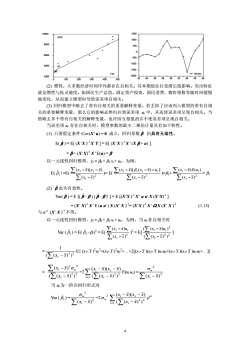
150010000401000800050006000-500-10004000-1500FDI?RESID-20008890929496n300200(2)惯性。大多数经济时间序列都存在自相关。其本期值往往受滞后值影响。突出特征就是惯性与低灵敏度。如国民生产总值，固定资产投资，国民消费，物价指数等随时间缓慢地变化，从而建立模型时导致误差项自相关。（3）回归模型中略去了带有自相关的重要解释变量。若丢掉了应该列入模型的带有自相关的重要解释变量，那么它的影响必然归并到误差项u中，从而使误差项呈现自相关。当然略去多个带有自相关的解释变量，也许因互相抵消并不使误差项呈现自相关。当误差项u存在自相关时，模型参数的最小二乘估计量具有如下特性。(1）只要假定条件Cov(X'u)=0成立，回归系数β仍具有无偏性。E(β)=E[(X'X)"X"Y]=E[(X'X)"x"(Xβ+u) ]=β+(X'X)"X"E(u)= β以一元线性回归模型，y=β+βx+u，为例E(A)-E(24-301-)= (2(-D1a(r-3)+l)-β+20-)E(c) Z(x, -x)2Z(x, -)2Z(x, -)2(2)β丧失有效性。Var(β)=E[(β-β)(β-β)]=E[(X"X)"x"uuX(X"x)"]=(XX)"X"E(uu)X(X"X)"=(X"X)"X"QX(X"X)(1.13)与2(X"X)"不等。以一元线性回归模型，y=β+βix+u，为例，当u非自相关时r(E(x,-x)u,)2Var(A)-E(-A)-E((-)-L%(Z(x, -x))2E(x, -x)?(,- (-)*+()+2() )+(1- )+)E(x, -)o.?a?+2)(,E(uus)(Z(x -x)2)2(Z(x, -x))2Z(x, -x)2当u为一阶自回归形式时2au2 (x, -X)(x, -对)Var(β)+2g.台(Z(x, -x)3)2(x, -x)24

2000 4000 6000 8000 10000 0 100 200 300 400 500 FDI GDP -2000 -1500 -1000 -500 0 500 1000 1500 82 84 86 88 90 92 94 96 98 RESID (2) 惯性。大多数经济时间序列都存在自相关。其本期值往往受滞后值影响。突出特征 就是惯性与低灵敏度。如国民生产总值，固定资产投资，国民消费，物价指数等随时间缓慢 地变化，从而建立模型时导致误差项自相关。 (3) 回归模型中略去了带有自相关的重要解释变量。若丢掉了应该列入模型的带有自相 关的重要解释变量，那么它的影响必然归并到误差项 ut 中，从而使误差项呈现自相关。当 然略去多个带有自相关的解释变量，也许因互相抵消并不使误差项呈现自相关。 当误差项 ut 存在自相关时，模型参数的最小二乘估计量具有如下特性。 (1) 只要假定条件 Cov(X ' u) = 0 成立，回归系数 β ˆ 仍具有无偏性。 E( ) = E[ (X 'X ) -1 X 'Y ] = E[ (X 'X ) -1 β X ' (X β + u) ]. ˆ = β + (X 'X) -1 X ' E(u) = β 以一元线性回归模型，yt = β0 + β1 xt + ut，为例， E( )=E( 1 ˆ β ∑ ∑ − −− 2 )( ))(( xx yyxx t tt )= E( ∑ ∑ − − +− 2 1 )( ])()[( xx uxxxx t t β t t )=β1+ ∑ ∑ − − 2 )( )()( xx uExx t t t = β1 (2) β ˆ 丧失有效性。 Var( ) = E [( - β ) ( - β )' ] = E [(X 'X ) -1 X ' u u' X (X 'X) -1 β ] ˆ β ˆ β ˆ = (X ' X) -1 X ' E (u u') X (X ' X ) -1= (X 'X ) -1 X ' Ω X (X ' X ) -1 (1.13) 与 (X ' X ) σ2 -1 不等。 以一元线性回归模型，yt = β0 + β1 xt + ut，为例，当 ut 非自相关时 Var ( ) = E( -β1) 2 = E( 1 ˆ β 1 ˆ β ∑ ∑ − − 2 )( )( xx uxx t tt ) 2 = E[ ∑ ∑ − − 22 2 ))(( ))(( xx uxx t tt ] = ∑ − 22 ))(( 1 xxt E{ (x1- x ) 2 u1 2 +(x2- x ) 2 u2 2 +.+2[(x1- x )(x2- x )u1u2+(x1- x )(x3- x )u1u3+.]} = ∑ ∑ − − 22 2 2 ))(( )( xx xx t t σ u +2∑< ∑ − − − st t t s xx xxxx 22 ))(( ))(( E(ut us) = ∑ − 2 2 xx )( t σ u 当 ut 为一阶自回归形式时 Var ( 1 ) = ˆ β ∑ − 2 2 xx )( t σ u +2 2 σ u ∑< ∑ − − − st t t s xx xxxx 22 ))(( ))(( ρ s-t 4

Oβ,的方差比u非自相关时大，失去有效性。因为OLS法仍然用估计β的Z(x, -3)?方差，而兴一)，一项常常是正的，所以会低估序的方差。Ks((x, -x))2B低估回归参数估计量的方差，等于夸大了回归参数的抽样精度（t1/ /Z(x, -)2过高的估计统计量1的值，从而把不重要的解释变量保留在模型里，使显著性检验失去意义。(3）有可能低估误差项u的方差。（4)Var(B阝）和s2都变大，都不具有最小方差性。所以用依据普通最小二乘法得到的回归方程去预测，预测是无效的。4.自相关检验下面介绍三种判别与检验方法。(1)图示法图示法就是依据残差u,对时间1的序列图作出判断。由于残差ü,是对误差项u的估计，所以尽管误差项u观测不到，但可以通过ü的变化判断u是否存在自相关。图示法的具体步骤是，（1）用给定的样本估计回归模型，计算残差i,，（t=1,2，..T)，绘制残差图；(2）分析残差图。若残差图与图1.1a类似，则说明ut不存在自相关；若与图1.1c类似，则说明u存在正自相关；若与图1.1e类似，则说明u存在负自相关。经济变量由于存在惯性，不可能表现出如图1.1e那样的震荡式变化。其变化形式常与图1.1中a相类似，所以经济变量的变化常表现为正自相关。(2）DW（Durbin-Watson）检验法DW检验是J.Durbin,GS.Watson于1950，1951年提出的。它是利用残差u,构成的统计量推断误差项u是否存在自相关。使用DW检验，应首先满足如下三个条件。（1）误差项u,的自相关为一阶自回归形式。（2）因变量的滞后值y-不能在回归模型中作解释变量。（3）样本容量应充分大（T>15）DW检验步骤如下。给出假设Ho:p=0(ut不存在自相关）Hi:p0(u存在一阶自相关)用残差值u,计算统计量DW。YZ(i, -it1)2DW=-2(1.14)Za?1=1其中分子是残差的一阶差分平方和，分母是残差平方和。把上式展开，5

1 ˆ β 的方差比 ut非自相关时大，失去有效性。因为 OLS 法仍然用 ∑ − 2 2 xx )( t σ u 估计 的 方差，而 1 ˆ β ∑ 15） DW 检验步骤如下。给出假设 H0: ρ = 0 (ut 不存在自相关) H1: ρ ≠ 0 (ut 存在一阶自相关) 用残差值 计算统计量 uˆt DW。 DW = ∑ ∑ = = − − T t t T t tt u uu 1 2 2 2 1 ˆ ( ˆˆ ) (1.14) 其中分子是残差的一阶差分平方和，分母是残差平方和。把上式展开， 5

2Eu,u-uZu-t=2=2DW=1=2(1.15)T因为当样本充分大时，有2Zi,(1.16)Ziu,-t=l(=21=2把（1.15）式中的有关项用上式中第2项代换7T22a. -22.ZiitDW~12t=2↑=2=2(1-(1.17))=2(1-p)TZi?2it=21=2因为p的取值范围是[-1,1]，所以DW统计量的取值范围是[0,4]。p与DW值的对应关系见表1.1。表 1.1p与DW值的对应关系及意义DWu的表现pDW=2P=0u非自相关DW=0p=1u完全正自相关DW=4P=-1u完全负自相关0<DW<20<p<1u有某种程度的正自相关2<DW<4-1<p<0u有某种程度的负自相关实际中DW=0,2,4的情形是很少见的。当DW取值在（0,2），（2,4）之间时，怎样判别误差项u是否存在自相关呢？推导统计量DW的精确抽样分布是困难的，因为DW是依据残差u,计算的，而ü,的值又与x的形式有关。DW检验与其它统计检验不同，它没有唯一的临界值用来制定判别规则。然而Durbin-Watson根据样本容量和被估参数个数，在给定的显著性水平下，给出了检验用的上、下两个临界值du和d。判别规则如下：不确不确拒绝Ho定区接受H。拒绝H。定区DW04d4-dwu4-d.图1.2（1）若DW取值在（O,d）之间，拒绝原假设Ho,认为u存在一阶正自相关。(2）若DW取值在（4-dl，4）之间，拒绝原假设Ho,认为ut存在一阶负自相关。(3）若DW取值在（du,4-du）之间，接受原假设Ho,认为ur非自相关。(4）若DW取值在（d.du）或（4-du.4-di）之间，这种检验没有结论，即不能判别u是否存在一阶自相关。判别规则可用图1.2表示。当DW值落在“不确定”区域时，有两种处理方法。①加大样本容量或重新选取样本，重作DW检验。有时DW值会离开不确定区。②选用其它检验方法。DW检验表4给出DW检验临界值。DW检验临界值与三个参数有关。①检验水平α，②样本容量T，③原回归模型中解释变量个数k（不包括常数项）。6

DW = ∑ ∑∑ ∑ = == = − −+ − T t t T t T t T t t t tt u uu uu 1 2 22 2 1 2 1 2 ˆ ˆˆ 2 ˆˆ (1.15) 因为当样本充分大时，有 ∑ ≈∑ ≈ (1.16) = T t t u 2 2 ˆ = − T t t u 2 2 1 ˆ ∑= T t t u 1 2 ˆ 把（1.15）式中的有关项用上式中第 2 项代换， DW ≈ ∑ ∑ ∑ = − = = − − − T t t T t T t t tt u u uu 2 2 1 2 2 1 2 1 ˆ 2 ˆ 2 ˆˆ = 2 (1 - ∑ ∑ = − = − T t t T t tt u uu 2 2 1 2 1 ˆ ˆˆ ) = 2 (1 - ρˆ ) (1.17) 因为 ρ 的取值范围是 [-1, 1]，所以 DW 统计量的取值范围是 [0, 4]。ρ 与 DW 值的对 应关系见表 1.1。 表 1.1 ρ 与 DW 值的对应关系及意义 ρ DW ut 的表现 ρ = 0 DW = 2 ut 非自相关 ρ = 1 DW = 0 ut 完全正自相关 ρ = -1 DW = 4 ut 完全负自相关 0 < ρ < 1 0 < DW < 2 ut 有某种程度的正自相关 -1 < ρ < 0 2 < DW < 4 ut 有某种程度的负自相关 实际中 DW = 0, 2, 4 的情形是很少见的。当 DW 取值在（0, 2），（2, 4）之间时，怎样判 别误差项 ut 是否存在自相关呢？推导统计量 DW 的精确抽样分布是困难的，因为 DW 是依 据残差 计算的，而 的值又与 xt 的形式有关。DW 检验与其它统计检验不同，它没有唯 一的临界值用来制定判别规则。然而 Durbin-Watson 根据样本容量和被估参数个数，在给定 的显著性水平下，给出了检验用的上、下两个临界值 dU和 dL 。判别规则如下： ut ˆ ut ˆ 图 1.2 (1) 若 DW 取值在（0, dL）之间，拒绝原假设 H0 ,认为 ut 存在一阶正自相关。 (2) 若 DW 取值在（4 - dL , 4）之间，拒绝原假设 H0 ,认为 ut 存在一阶负自相关。 (3) 若 DW 取值在（dU, 4- dU）之间，接受原假设 H0 ,认为 ut 非自相关。 (4) 若 DW 取值在（dL, dU）或（４- dU, 4 - dL）之间，这种检验没有结论，即不能判别 ut 是否存在一阶自相关。判别规则可用图 1.2 表示。 当 DW 值落在“不确定”区域时，有两种处理方法。①加大样本容量或重新选取样本， 重作 DW 检验。有时 DW 值会离开不确定区。②选用其它检验方法。 DW 检验表 4 给出 DW 检验临界值。DW 检验临界值与三个参数有关。①检验水平α， ②样本容量 T , ③原回归模型中解释变量个数 k（不包括常数项）。 6

注意：因为DW统计量是以解释变量非随机为条件得出的，所以当有滞后的内生变量作解释变量时，DW检验无效。这时的表现是DW值常常接近2。当估计式为yi=Bo+BiyiI+βx+ur时，Durbin认为应该用下面的h统计量检验一阶自相关。TTDWh=p(1(1-2i-T(Var(B)V1-T(Var(B,))Durbin已证明h统计量近似服从均值为零方差为1的标准正态分布。可以用标准正态分布临界值对h的显著性作出检验。注意：当T(Var(β,)>1 时检验无效。②不适用于联立方程模型中各方程的序列自相关检验。③DW统计量不适用于对高阶自相关的检验。(3）LM检验（亦称BG检验）法DW统计量只适用于一阶自相关检验，而对于高阶自相关检验并不适用。利用BG统计量可建立一个适用性更强的自相关检验方法，既可检验一阶自相关，也可检验高阶自相关。BG检验由Breusch-Godfrey提出。BG检验是通过一个辅助回归式完成的，具体步骤如下。对于多元回归模型(6.18)y=Bo+Bixi,+βx2,+ ... +βk-1x a-1t+u考虑误差项为n阶自回归形式(6.19)u,=pi u-I +... + Pn u-n + vt其中v，为随机项，符合各种假定条件。零假设为Ho: PI = P2 =...= Pn= 0这表明u不存在n阶自相关。用估计（6.18）式得到的残差建立辅助回归式i,=put--+...+pnitn+Bo+βixi,+βx2t+ ... +βk-1xk-li+v(6.20)上式中的i,是（6.18）式中u的估计值。估计上式，并计算可决系数R。构造LM统计量，LM=TR?(6.21)其中T表示（6.18）式的样本容量。R2为（6.20）式的可决系数。在零假设成立条件下，LM统计量渐近服从(m分布。其中n为（6.19）式中自回归阶数。如果零假设成立，LM统计量的值将很小，小于临界值。判别规则是，若LM=TR≤x(n)，接受Ho;若LM=TR>(m)，拒绝Ho;(4)回归检验法回归检验法的优点是，（1）适合于任何形式的自相关检验，（2）若结论是存在自相关，则同时能提供出自相关的具体形式与参数的估计值。缺点是计算量大。回归检验法的步骤如下：①用给定样本估计模型并计算残差u,。②对残差序列i,，（t=1,2，…，T）用普通最小二乘法进行不同形式的回归拟合。如u,=p u,-i+viu,=pi u,-1+p2 i,-2+v7

注意： ①因为 DW 统计量是以解释变量非随机为条件得出的，所以当有滞后的内生变量作解 释变量时，DW 检验无效。这时的表现是 DW 值常常接近 2。当估计式为 yt = β0 + β1 yt-1 + β2 xt + ut 时，Durbin 认为应该用下面的 h 统计量检验一阶自相关。 h = ρˆ = (1- 2 DW ) )) ˆ ((1 VarT β1 T )) − ˆ ((1 VarT β1 T − Durbin 已证明 h 统计量近似服从均值为零方差为 1 的标准正态分布。可以用标准正态 分布临界值对 h 的显著性作出检验。注意：当 VarT (( β ˆ 1 )) >1 时检验无效。 ②不适用于联立方程模型中各方程的序列自相关检验。 ③DW 统计量不适用于对高阶自相关的检验。 (3) LM 检验（亦称 BG 检验）法 DW 统计量只适用于一阶自相关检验，而对于高阶自相关检验并不适用。利用 BG 统计 量可建立一个适用性更强的自相关检验方法，既可检验一阶自相关，也可检验高阶自相关。 BG 检验由 Breusch-Godfrey 提出。BG 检验是通过一个辅助回归式完成的，具体步骤如下。 对于多元回归模型 yt = β0 + β1x1 t + β2 x2 t + . + β k –1 x k-1 t + ut (6.18) 考虑误差项为 n 阶自回归形式 ut = ρ1 ut-1 + . + ρn ut - n + vt (6.19) 其中 vt 为随机项，符合各种假定条件。零假设为 H0: ρ1 = ρ2 = .= ρn = 0 这表明 ut 不存在 n 阶自相关。用估计（6.18）式得到的残差建立辅助回归式， uˆt = 1 ρˆ 1 ˆ t− u + . + ρ n ˆ u −nt ˆ +β0 +β1x1 t +β2 x2 t + . + β k –1 x k-1 t + vt (6.20) 上式中的 是（6.18）式中 ut 的估计值。估计上式，并计算可决系数 R uˆt 2 。构造 LM 统计量， LM = T R2 (6.21) 其中 T 表示（6.18）式的样本容量。R2为（6.20）式的可决系数。在零假设成立条件下，LM 统计量渐近服从 χ 2 (n) 分布。其中 n 为（6.19）式中自回归阶数。如果零假设成立，LM 统计 量的值将很小，小于临界值。 判别规则是，若 LM = T R2 ≤ χ 2 (n)，接受 H0； 若 LM = T R2 > χ 2 (n)，拒绝 H0； (4) 回归检验法 回归检验法的优点是，（1）适合于任何形式的自相关检验，（2）若结论是存在自相关， 则同时能提供出自相关的具体形式与参数的估计值。缺点是计算量大。回归检验法的步骤如 下： ①用给定样本估计模型并计算残差 。ut ˆ ②对残差序列uˆt , (t = 1 ,2 ,. , T ) 用普通最小二乘法进行不同形式的回归拟合。如 ut ˆ = ρ – 1 + vt ut ˆ ut ˆ = ρ1 ut – 1 + ρ2 – 2 + vt ˆ ut ˆ 7

u,=pu,-1+vu,=pya-+v(3）对上述各种拟合形式进行显著性检验，从而确定误差项u，存在哪一种形式的自相关。5.克服自相关如果模型的误差项存在自相关，首先应分析产生自相关的原因。如果自相关是由于错误地设定模型的数学形式所致，那么就应当修改模型的数学形式。怎样查明自相关是由于模型数学形式不妥造成的？一种方法是用残差i，对解释变量的较高次幂进行回归，然后对新的残差作DW检验，如果此时自相关消失，则说明模型的数学形式不妥。如果自相关是由于模型中省略了重要解释变量造成的，那么解决办法就是找出略去的解释变量，把它做为重要解释变量列入模型。怎样查明自相关是由于略去重要解释变量引起的？一种方法是用残差t，对那些可能影响因变量但又未列入模型的解释变量回归，并作显著性检验，从而确定该解释变量的重要性。如果是重要解释变量，应该列入模型。只有当以上两种引起自相关的原因都消除后，才能认为误差项u“真正”存在自相关。在这种情况下，解决办法是变换原回归模型，使变换后的随机误差项消除自相关，进而利用普通最小二乘法估计回归参数。这种变换方法称作广义最小二乘法。下面介绍这种方法。设原回归模型是yi=βo+Bixir+Bx2t+.-+βkx k+u(1.19)(t=1, 2, ..., T)其中u具有一阶自回归形式u,=pu-i +vi其中v，满足通常的假定条件，把上式代入（1.19）式，(1.20)y=βo+Bix1++βx2,+... +oxkr+pur-1 + v求模型（1.19）的（t-1）期关系式，并在两侧同乘p(1.21)pyt-I=pβo+pβix1t-I+pβx21-I+...+pPexkt-1 +put-1用（1.19）式与上式相减得(1.22)yt-pyt-I=βo(1 -p) +Bi(xir-pxi-l)+...+Br(Xkt-pxkt-1)+ vt令(1.23)y*=yr-pyt-l,(1.24)x*=xi-pxt-, j=1,2,..kβ*=βo (1 -p),(1.25)则模型（1.22）表示如下，y*=B*+βx*+Bx2 *+... +βx*+V(1=2,3..T)(1.26)上述变换称作广义差分变换。上式中的误差项v是非自相关的，满足假定条件，所以可对上式应用最小二乘法估计回归参数。所得估计量具有最佳线性无偏性。上式中的β..限就是原模型（1.19）中的βi..，而B*与模型（1.19）中的β有如下关系β*=βo(1 -p),βo=β* / (1-p)(1.27)注意：（1）对（1.19）式进行OLS估计得到的β.B，，β的估计量称作普通最小二乘估计量；对（1.26）式进行OLS估计得到的B,β，，，β的估计量称作广义最小二乘估计量。8

ut ˆ = ρ - 1 2 ut + v t ˆ ut ˆ = ρ 1 ˆut− + vt . (3) 对上述各种拟合形式进行显著性检验，从而确定误差项 ut 存在哪一种形式的自相 关。 5. 克服自相关 如果模型的误差项存在自相关，首先应分析产生自相关的原因。如果自相关是由于错误 地设定模型的数学形式所致，那么就应当修改模型的数学形式。怎样查明自相关是由于模型 数学形式不妥造成的？一种方法是用残差 对解释变量的较高次幂进行回归，然后对新的 残差作 DW 检验，如果此时自相关消失，则说明模型的数学形式不妥。 ut ˆ 如果自相关是由于模型中省略了重要解释变量造成的，那么解决办法就是找出略去的解 释变量，把它做为重要解释变量列入模型。怎样查明自相关是由于略去重要解释变量引起 的？一种方法是用残差 对那些可能影响因变量但又未列入模型的解释变量回归，并作显 著性检验，从而确定该解释变量的重要性。如果是重要解释变量，应该列入模型。 ut ˆ 只有当以上两种引起自相关的原因都消除后，才能认为误差项 ut “真正”存在自相关。 在这种情况下，解决办法是变换原回归模型，使变换后的随机误差项消除自相关，进而利用 普通最小二乘法估计回归参数。这种变换方法称作广义最小二乘法。下面介绍这种方法。 设原回归模型是 yt = β0 + β1x1 t + β2 x2 t+ . + β k x k t + ut (t = 1, 2, ., T ) (1.19) 其中 ut 具有一阶自回归形式 ut = ρ ut-1 + vt 其中 vt 满足通常的假定条件，把上式代入（1.19）式， yt = β0 + β1 x1 t +β2 x2 t + . + β0 xk t + ρ ut - 1 + vt (1.20) 求模型（1.19）的 (t - 1) 期关系式，并在两侧同乘 ρ， ρ yt -1= ρ β0 + ρ β1 x1 t -1 + ρ β2 x2 t -1 + . + ρ βk xk t - 1 + ρ ut - 1 (1.21) 用（1.19）式与上式相减得 yt - ρ yt -1 = β0 (1 - ρ) + β1 (x1t - ρ x1 t-1) +. + βk ( xk t - ρ xk t -1) + vt (1.22) 令 yt* = yt - ρ yt -1 , (1.23) xj t* = xj t - ρ xj t - 1, j = 1 , 2 , . k (1.24) β0* = β0 (1 - ρ ), (1.25) 则模型（1.22）表示如下， yt* = β0*+ β1 x1 t* + β2 x2 t* +. + βk xk t* + vt ( t = 2 , 3 ,. T ) (1.26) 上述变换称作广义差分变换。上式中的误差项 vt是非自相关的，满足假定条件，所以可 对上式应用最小二乘法估计回归参数。所得估计量具有最佳线性无偏性。上式中的 β1 . βk 就是原模型（1.19）中的 β1 . βk，而 β0* 与模型（1.19）中的 β0 有如下关系， β0* = β0 (1 - ρ), β0 = β0* / (1 - ρ) (1.27) 注意： （1）对（1.19）式进行 OLS 估计得到的β0, β1, . , β k的估计量称作普通最小二乘估计 量；对（1.26）式进行 OLS 估计得到的β0, β1, , . , β k的估计量称作广义最小二乘估计量。 8

下图是以如下一元线性回归模型y,=0.5+0.8x,+ut，u=ut-1+Vt为基础用蒙特卡罗模拟方法给出四条关于β的半个置信区间的收敛曲线。由上至下四条收敛曲线的设定条件见下表：收敛曲线dix,估计方法T=50时的收敛相对比率1=0.7（有自相关）I(1)+tOLS2.712GLS2.09=0.7（有自相关）I(1)+t3OLS1.20I(1)=0（非自相关）4OLS1.00=0（非自相关）I(1)+t注：（1）由设定条件知y与x，存在协整关系。（2）下图横轴表示样本容量。曲线到横轴的垂直距离为置信区间半径（收敛于真值的半径）曲线①、②、③、④的收敛相对比率是以曲线④的置信区间半径为1的计算结果。图中可见样本容量越大估计越准确。自相关条件下GLS估计量优于OLS估计量。@2R4图1.3图中横轴表示样本容量。曲线到横轴的垂直距离为置信区间半径（收敛于真值的半径）。（2）这种广义差分变换损失了一个观测值，样本容量变成（T-1）。为避免这种损失，K.R.Kadiyala（1968）提出对y,与xj，的第一个观测值分别作如下变换。y*=yi/1-p2Xj1*=x1/i-p?,(j=1,2,..k)于是对模型（1.26），样本容量仍然为T。这种变换的目的就是使相应误差项u的方差与其它误差项u2,u3...ut,的方差保持相等。作上述变换后，有u*= u yl-p?则Var(u*)=(1 - p) Var(ui)把（1.10）式代入上式，Var(u1*) =(1 - p?) [α,2 / (1 - p2)] = g,2u与其他随机误差项的方差相同。（3）当误差项u的自相关具有高阶自回归形式时，仍可用与上述相类似的方法进行广9

下图是以如下一元线性回归模型 yt = 0.5 + 0.8 xt + ut ， ut = φ1 ut-1 + vt 为基础用蒙特卡罗模拟方法给出四条关于β1 的半个置信区间的收敛曲线。由上至下四条收敛 曲线的设定条件见下表： 收敛曲线 φ1 xt 估计方法 T = 50 时的收敛相对比率 1 φ1=0.7（有自相关） I(1)+t OLS 2.71 2 φ1=0.7（有自相关） I(1)+t GLS 2.09 3 φ1=0 （非自相关） I(1) OLS 1.20 4 φ1=0 （非自相关） I(1)+t OLS 1.00 注：（1）由设定条件知 yt 与 xt 存在协整关系。 （2）下图横轴表示样本容量。曲线到横轴的垂直距离为置信区间半径（收敛于真值的半径）。 曲线①、②、③、④的收敛相对比率是以曲线④的置信区间半径为 1 的计算结果。图中 可见样本容量越大估计越准确。自相关条件下 GLS 估计量优于 OLS 估计量。 图 1.3 图中横轴表示样本容量。曲线到横轴的垂直距离 为置信区间半径（收敛于真值的半径）。 （2）这种广义差分变换损失了一个观测值，样本容量变成（T- 1）。为避免这种损失， K. R. Kadiyala（1968）提出对 yt 与 xj t的第一个观测值分别作如下变换。 y1* = y1 2 1− ρ x j 1* = xj 1 2 1− ρ , ( j = 1 , 2 , . k ) 于是对模型（1.26），样本容量仍然为 T。 这种变换的目的就是使相应误差项 u1 的方差与其它误差项 u2, u3,.uT,的方差保持相等。 作上述变换后，有 u1* = u1 2 1− ρ 则 Var(u1*) = (1 - ρ 2 ) Var(u1) 把（1.10）式代入上式， Var(u1*) = (1 - ρ 2 ) [σv 2 / (1 - ρ 2 )] = σv 2 u1 与其他随机误差项的方差相同。 （3）当误差项 ut 的自相关具有高阶自回归形式时，仍可用与上述相类似的方法进行广 9

义差分变换。比如u具有二阶自回归形式，u=piui-1+p2u-2+V,则变换过程应首先求出原模型（t-1）期与（t-2）期的两个关系式，然后利用与上述相类似的变换方法建立符合假定条件的广义差分模型。若u具有k阶自回归形式，则首先求k个不同滞后期的关系式，然后通过广义差分变换使模型的误差项符合假定条件。需要注意的是对二阶自回归形式，作广义差分变换后，要损失两个观测值；对k阶自回归形式，作广义差分变换后，将损失k个观测值。（4）当用广义差分变量回归的结果中仍存在自相关时，可以对广义差分变量继续进行广义差分直至回归模型中不存在自相关为止。6.克服自相关的矩阵描述对于线性回归模型Y=Xβ+u(1.28)假定E(uu)=I不成立。误差项u具有一阶自回归形式自相关，u,=put-i+v,则Cov(u）由（1.12）式给出1P1pCov(u)= E(u u')= Q= ouT-1其中2=,2/(1-p)。取o1[Vi-p?1-pM=（按K.R.Kadiyala提议补上第一个观测值）10-p ]使MQM'=0,1(1.29)用M左乘模型（1.28），MY-MXB+Mu(1.30)令y*=MY,X*=MX,u*=Mu则模型（1.30）表示为Y* =X*β+ u*(1.31)其中10

义差分变换。比如 ut 具有二阶自回归形式， ut = ρ1 ut- 1 + ρ 2 ut– 2 + vt , 则变换过程应首先求出原模型（t-1）期与（t-2）期的两个关系式，然后利用与上述相类似 的变换方法建立符合假定条件的广义差分模型。若 ut 具有 k 阶自回归形式，则首先求 k 个不 同滞后期的关系式，然后通过广义差分变换使模型的误差项符合假定条件。 需要注意的是对二阶自回归形式，作广义差分变换后，要损失两个观测值；对 k 阶自回 归形式，作广义差分变换后，将损失 k 个观测值。 （4）当用广义差分变量回归的结果中仍存在自相关时，可以对广义差分变量继续进行 广义差分直至回归模型中不存在自相关为止。 6. 克服自相关的矩阵描述 对于线性回归模型 Y = Xβ + u (1.28) 假定 E(u u ') = σ 2 I 不成立。误差项 ut 具有一阶自回归形式自相关， ut = ρ u t -1 + vt 则 Cov(u) 由 (1.12) 式给出 Cov(u) = E(u u ' ) = Ω = σu 2 ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ −− − − − 1. . 1 . 1 . 321 1 2 1 TT T T T ρρρ ρ ρρ ρρρ 其中σu 2 = σv 2 / (1 - ρ 2 )。取 M = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − 0 1 1 . 1 1 0 2 ρ ρ ρ （按 K. R. Kadiyala 提议补上第一个观测值） 使 M Ω M ' = σv 2 I (1.29) 用 M 左乘模型（1.28）， M Y = M X β + M u (1.30) 令 Y* = M Y, X* = M X, u* = M u 则模型（1.30）表示为 Y* = X*β + u* (1.31) 其中 10