《计量经济学》课程授课教案（讲稿）03 多元线性回归模型

1.3多元线性回归与最小二乘估计1.假定条件、最小二乘估计量和高斯一马尔可夫定理多元线性回归模型：(1.1)y,=B+Bix+Bax+...+B-ixrk-I+u其中y是被解释变量（因变量），xj是解释变量（自变量），u是随机误差项，β，i=0,1，…，k-1是回归参数（通常未知）。对经济问题的实际意义：y与x,存在线性关系，Xj，j=0,1，…，k-1，是y的重要解释变量。u代表众多影响y变化的微小因素。使y的变化偏离了E(y)=β+βixa+βxe+.+1X1k-1决定的k维空间平面。当给定一个样本（yt，x，xexk-1），t=1,2，,T时，上述模型表示为yi=β+Bxn+Bx12+.+ik-1+ut，经济意义：xu,是y的重要解释变量。y2=B+βix21+Bax22+.+B-1X2k-1+u2，代数意义：y与xt,存在线性关系。几何意义：y表示一个多维平面。(1.2)y =B+BixTI+βx T2 +...+-iX Tk-I+uT此时y与xt已知，β与u未知。1[y]βoXjXI k=IuyβIy21uX21X2 k-X2j(1.3):：..1XTTLβk-I J(kxl)Lyr J(Tx)XTXT k-l[ur J(Tx1)Y=Xβ+u(1.4)为保证得到最优估计量，回归模型（1.4）应满足如下假定条件。假定（1）随机误差项u是非自相关的，每一误差项都满足均值为零，方差相同且为有限值，即[10000.0Var(u)=E(a")== 2E(u)=0[001[o]假定(2）解释变量与误差项相互独立，即E(X'u)= 0假定（3）解释变量之间不存在完全线性关系，即X或X'X是满秩的矩阵。rk(X'X) = rk(X) = k其中rk()表示矩阵的秩。假定(4）解释变量是非随机的，且当T→α时T'xX-Q其中Q是一个有限值的非退化矩阵。最小二乘（OLS）法的原理是求残差（误差项的估计值）平方和最小。代数上是求极值问题。1

1.3 多元线性回归与最小二乘估计 1．假定条件、最小二乘估计量和高斯—马尔可夫定理 多元线性回归模型： yt = β0 +β1xt1 + β2xt2 +.+ βk- 1xt k -1 + ut (1.1) 其中 yt 是被解释变量（因变量），xt j 是解释变量（自变量），ut 是随机误差项，βi, i = 0, 1, . , k - 1 是回归参数（通常未知）。 对经济问题的实际意义：yt 与 xt j 存在线性关系，xt j, j = 0, 1, . , k - 1, 是 yt 的重要解释 变量。ut 代表众多影响 yt变化的微小因素。使 yt 的变化偏离了 E( yt) = β0 +β1xt1 + β2xt2 +.+ βk- 1xt k -1 决定的 k 维空间平面。 当给定一个样本（yt , xt1, xt2 ,., xt k -1）, t = 1, 2, ., T 时, 上述模型表示为 y1 = β0 +β1x11 + β2x12 +.+ βk- 1x1 k -1 + u1, 经济意义：xt j 是 yt 的重要解释变量。 y2 = β0 +β1x21 + β2x22 +.+ βk- 1x2 k -1 + u2, 代数意义：yt与 xt j 存在线性关系。 . 几何意义：yt 表示一个多维平面。 yT = β0 +β1x T 1 + β2x T 2 +.+ βk- 1x T k -1 + uT (1.2) 此时 yt 与 x t i已知，βj 与 ut 未知。 )1( 2 1 1 )1( 1 0 )( 1 1 21 2 12 11 1 11 )1( 2 1 1 1 1 × − × × − − − × ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ kT k k T T T Tj kT j k j k T T u u u xxx xxx xxx y y y # # " " """""" " " " " # β β β (1.3) Y = X β + u , (1.4) 为保证得到最优估计量，回归模型（1.4）应满足如下假定条件。 假定 ⑴ 随机误差项 ut 是非自相关的，每一误差项都满足均值为零，方差 σ 2 相同且 为有限值，即 E(u) = 0 = , Var (u) = E( ' ) = σ 2 I = σ 2 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 # uˆ uˆ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 100 00 001 % 假定 ⑵ 解释变量与误差项相互独立，即 E(X 'u) = 0 假定 ⑶ 解释变量之间不存在完全线性关系，即 X 或 X 'X 是满秩的矩阵。 rk(X 'X) = rk(X) = k 其中 rk(⋅)表示矩阵的秩。 假定⑷ 解释变量是非随机的，且当 T → ∞ 时 T– 1X 'X → Q 其中 Q 是一个有限值的非退化矩阵。 最小二乘 (OLS) 法的原理是求残差（误差项的估计值）平方和最小。代数上是求极值 问题。 1

minS=(Y-Xβ)(Y-xp)=Y'Y-β'X'Y-Y"xβ+β'X'Xβ=Y'Y-2B'X'Y+B'X'XB(1.5)因为Y'Xβ是一个标量，所以有Y"Xβ=βX'Y。（1.5）的一阶条件为S= -2X'Y+2XXβ=0(1.6)ap化简得X'Y=X'XB因为(X'X）是一个非退化矩阵（见假定(3)），所以有β=(X'X)" X"Y(1.7)因为X的元素是非随机的，(X'X)-X是一个常数矩阵，则B是Y的线性组合，为线性估计量。求出β，估计的回归模型写为Y=x+a(1.9)其中β=（β。β：βk-I）是β的估计值列向量，a=(Y-Xβ）称为残差列向量。因为a=Y-Xβ= Y-X(X'X)'x'Y=[I-X(X'X)"X'JY(1.10)所以也是Y的线性组合。β的期望和方差是E(β)=E[(X'X)"x'Y]= E[(X'X)'X'(Xβ +u)]=β +(X'X)"'X'E(u)=β(1.11)Var(β)=E[(β-β(β-β)]=E[(X'X)"x'uux(X"X)"-E[(X"X)"X"IX(X"X)"] = ?(X"X)(1.12)高斯一马尔可夫定理：若前述假定条件成立，OLS估计量是最佳线性无偏估计量。β具有无偏性。β具有最小方差特性。β具有一致性，渐近无偏性和渐近有效性。2.残差的方差s=a'a/(T-k)(1.13)2是。2的无偏估计量，E(s2)=2。β的估计的方差协方差矩阵是Var(B)=$ (XX)l(1.14)3.多重确定系数（多重可决系数）Y=XB+a-Y+a(1.15)总平方和2

minS = (Y - X )' (Y - X ) = Y ' Y - X 'Y - Y ' X + β ˆ β ˆ β ˆ β ˆ ' β ˆ 'X 'X β ˆ = Y 'Y - 2 'X ' β Y + X 'X (1.5) ˆ β ˆ ' β ˆ 因为 Y 'X β 是一个标量，所以有 Y 'X = X 'Y。(1.5) 的一阶条件为： ˆ β ˆ β ˆ ' β ˆ ∂ ∂S = - 2X 'Y + 2X 'X β = 0 (1.6) ˆ 化简得 X 'Y = X 'X β ˆ 因为 (X 'X) 是一个非退化矩阵（见假定⑶），所以有 β ˆ = (X 'X) -1 X 'Y （1.7） 因为 X 的元素是非随机的，(X 'X) -1X 是一个常数矩阵，则 是 Y 的线性组合，为线性 估计量。 β ˆ 求出 ，估计的回归模型写为 β ˆ Y = X β + u (1.9) ˆ ˆ 其中 β = ( . )' 是 β 的估计值列向量， = (Y - X ) 称为残差列向量。因为 ˆ 0 ˆ β 1 ˆ β 1 ˆ β k− uˆ β ˆ uˆ = Y - X = Y - X (X 'X) -1X 'Y = [I - X (X 'X) -1 β X ' ]Y (1.10) ˆ 所以 也是 uˆ Y 的线性组合。 的期望和方差是 β ˆ E( ) = E[(X 'X) -1 X ' Y ] = E[(X 'X) -1 β X '(Xβ + u)] ˆ = β + (X 'X) -1X ' E(u) = β (1.11) Var( ) = E[( –β) ( –β)']= E[(X 'X) -1X ' u u' X (X 'X) -1 β ] ˆ β ˆ β ˆ = E[(X 'X) -1X ' σ 2 I X (X 'X) -1] = σ 2 (X 'X) -1 (1.12) 高斯—马尔可夫定理：若前述假定条件成立，OLS 估计量是最佳线性无偏估计量。 具 有无偏性。 具有最小方差特性。 具有一致性，渐近无偏性和渐近有效性。 β ˆ β ˆ β ˆ 2. 残差的方差 s 2 = uˆ ' uˆ / (T - k) (1.13) s 2 是σ 2 的无偏估计量，E(s 2 ) =σ 2 。 的估计的方差协方差矩阵是 β ˆ ∧ Var ( ) = s 2 (X 'X) -1 β (1.14) ˆ 3. 多重确定系数（多重可决系数） Y = X β + u = ˆ ˆ Yˆ + uˆ (1.15) 总平方和 2

SST-2L(0 -?-EL/3?-EL, 2,3+EL33-E?-2EJ,+?=YY-T2,(1.16)其中』是的样本平均数，定义为=（)/T。同理，回归平方和为SSR=TO,-D)?= PP-T?(1.17)其中立的定义同上。残差平方和为SSE= (,-)?= ZLa?= a'a(1.18)则有如下关系存在，SST= SSR + SSE(1.19)SSR_Y-Ty?R2=(1.20)SST"YY-Ty?显然有0≤R2≤1。R2→1，拟合优度越好。4.调整的多重确定系数当解释变量的个数增加时，通常R?不下降，而是上升。为调整因自由度减小带来的损失，又定义调整的多重确定系数R?如下：SSE I(T -k)T-1SST-SSRT-1R2 =1-(1 R)(1.21)=1T-kSSTT-kSST I(T-1)5.OLS估计量的分布若u～N(O,。1），则每个u都服从正态分布。于是有Y~N(XB,)(1.22)因B也是u的线性组合（见公式1.7），依据（1.11）和（1.12）有β~N(β(X'X)")(1.23)6.方差分析与F检验与SST相对应，自由度T-1也被分解为两部分(T-1) =(k-1)+(T- k)(1.24)SSRSSE回归均方定义为MSR=误差均方定义为MSE=k-1T-k表1.1方差分析表平方和自由度均方方差来源回归k-1MSR = SSR / (k-1)SSR=yy-Ty?误差SSE=a'aT-kMSE = SSE / (T-k)SST= YY-Tj?T-1总和3

SST =∑ = − T t t yy 1 2 )( =∑ ∑ = = ∑ = − + T t T t T t t t y yyy 1 2 1 1 2 2 = 2 1 1 2 2 yTyyy T t T t ∑ ∑ t − t + = = = Y 'Y - T 2 y , (1.16) 其中 y 是 yt 的样本平均数，定义为 y = Ty 。同理，回归平方和为 T t t /)(∑ =1 SSR = ∑ = − T t t yy 1 2 ( ˆ ) = Yˆ 'Yˆ - T 2 y (1.17) 其中 y 的定义同上。残差平方和为 SSE = ∑ = = ' (1.18) = − T t tt yy 1 2 ( ˆ ) ∑ = T t t u 1 2 ˆ uˆ uˆ 则有如下关系存在， SST = SSR + SSE (1.19) R2 = 2 ˆˆ 2 yT yT SST SSR -YY Y'Y ′ − = (1.20) 显然有 0 ≤ R 2 ≤ 1。R 2 →1，拟合优度越好。 4. 调整的多重确定系数 当解释变量的个数增加时，通常 R2 不下降，而是上升。为调整因自由度减小带来的损 失，又定义调整的多重确定系数 2 R 如下： 2 R = 1 - )( ) 1 (1 )1/( )/( SST SSRSST kT T TSST kTSSE − − − −= − − = 1 - )1( 1 2 R kT T − − − (1.21) 5. OLS 估计量的分布 若 u ∼ N (0, σ 2 I ) ，则每个 ut 都服从正态分布。于是有 Y ∼ N (Xβ, σ 2 I ) (1.22) 因 也是 β ˆ u 的线性组合（见公式 1.7），依据（1.11）和（1.12）有 β ˆ ∼ N ( β, σ 2 (X 'X) -1 ) (1.23) 6. 方差分析与 F 检验 与 SST 相对应，自由度 T-1 也被分解为两部分， （T-1）= (k -1) + (T- k) (1.24) 回归均方定义为 MSR = k −1 SSR ，误差均方定义为 MSE = kT SSE − 表 1.1 方差分析表 方差来源 平方和 自由度 均方 回归 SSR =Y 'Y -T ˆ ˆ y 2 k-1 MSR = SSR / (k-1) 误差 SSE = uˆ ' uˆ T-k MSE = SSE / (T-k) 总和 SST= Y 'Y - T y 2 T-1 3

Ho: β=β=..=β-I =0;Hi:β不全为零MSR-SSR/(k-1)F=~ F(&-1,T-k)(1.25)MSESSE/(T-k)设检验水平为α，则检验规则是，若F≤Fα(k-1,T-k)，接受Ho；若F>Fα(k-1,T-k)，拒绝Ho。a/2a2a/2Fa(k-1,T-k)-ta(Fi)ta(T-k)0图3.1F检验示意图图3.21检验示意图7. 1 检验Ho: β,=0, (i=1,2,,k-1), Hi: β +0Bβ, / Jvar(β) j++ =β, / /s(X"X)-j1 ~ (T-k)(1.26)s(βB,)判别规则：若|la(7-k)拒绝Ho。8.B的置信区间（1）全部β的联合置信区间接受F=(β-β)(X)(β-β)/ 2~Fa(,Tk)(1.27)(β-β)(XX)(β-β)≤skFα(hT-k)，它是一个k维椭球。(1.28)（2）单个B的置信区间β= β,+ /vj s tan(T-k) :(1.29)9. 预测（1）点预测(1.30)C=(1 X7+11 XT+12 ... XT+1k-1 )则T+1期被解释变量yT+1的点预测式是，JT+=cp-βo+βi x+11+.. +β kI X+1k!(1.31)（2）E(yT+1）的置信区间预测首先求点预测式cβ的抽样分布E(jT+1)=E(Cβ) =Cβ(1.32)Var(jT+1) = Var(Cβ) =E[(Cβ-Cβ)(Cβ-Cβ)')=E[C(β-β)[C(β-β)]'}-CE[(β-β)(β-β)"JC4

H0: β1= β2 = . = βk-1 = 0; H1: βj 不全为零 F = MSE MSR = )/( )1/( kTSSE kSSR − − ∼ F(k-1,T-k) (1.25) 设检验水平为α，则检验规则是，若 F ≤ Fα(k-1,T-k)，接受 H0；若 F > Fα(k-1,T-k) , 拒绝 H0。 图 3.1 F 检验示意图 图 3.2 t 检验示意图 7．t 检验 H 0：βj = 0, (j = 1, 2, ., k-1), H 1：βj ≠ 0 t = ) ˆ ( ˆ j j s β β = 1 2 1 1 )'( ˆ )ˆ ( ˆ + − + = j j jj β Var β β s XX ∼ t(T-k) (1.26) 判别规则：若⏐ t ⏐≤ tα(Τ−k) 接受 H 0；若⏐ t ⏐> tα(Τ−k) 拒绝 H 0。 8．βi 的置信区间 （1） 全部βi 的联合置信区间接受 F = k 1 (β - )' (X 'X) (β - ) / s 2 ∼ Fα (k, T-k) β (1.27) ˆ β ˆ ( β - )' (X 'X ) ( β - ) ≤ s 2 β k Fα (k, T-k)，它是一个 k 维椭球。 (1.28) ˆ β ˆ （2） 单个βi 的置信区间 βi = β i ± ˆ j+1 v s tα/2(Τ−k) . (1.29) 9．预测 （1）点预测 C = (1 xT+1 1 xT+1 2 . xT+1 k-1 ) (1.30) 则 T + 1 期被解释变量 yT+1 的点预测式是， 1 ˆT + y = C β = 0 + 1 xT+1 1 + . + k-1 xT+1 k-1 (1.31) ˆ β ˆ β ˆ β ˆ （2）E(yT+1) 的置信区间预测 首先求点预测式 C β 的抽样分布 ˆ E( ) yˆT +1 = E(C β ) = Cβ (1.32) ˆ Var( ) = Var(C ) = E[(C - Cβ ) (C - Cβ ) ' ] 1 ˆT + y β ˆ β ˆ β ˆ = E[C ( β - β ) [C ( - β )] ' ]= C E[( - β ) ( - β ) ' ]C ' ˆ β ˆ β ˆ β ˆ 4

=CVar(β)C'=C (X'X)'c"=C(X'X)'c(1.33)因为β服从多元正态分布，所以Cβ也是一个多元正态分布变量，即JT+I=Cβ~N(CB C(XX)"C)(1.34)构成1分布统计量如下C-Cβ1=JT+I-E(T+L) _-(1.35)I(T-R)sc(Xx)'csc(x'x)-'cCβ± ta2(, T-k) s c(x'x)-c置信区间(1.36)(3）单个yT+1的置信区间预测yT+I值与点预测值>T+有以下关系(1.37)yT+I= T+I+ U7+1其中ut+1是随机误差项。因为(1.38)E(yT+1)=E(yT+I+ UT+1)=CβVar( yT+1)= Var(J+I) + Var(uT+1) = α? C(XX)'C'+ ?= α? (C(X'X)'C"+ 1)(1.39)因为β服从多元正态分布，所以yT+I也是一个多元正态分布变量，即yT+1 ~ N (Cβ, αC(X'X)'C'+ 1)与上相仿，单个yT+1的置信区间是Cβ ± tal2(T-k) S /c(X'X)-'C'+1(1.40)计算举例：（见《计量经济分析》第19-27页，熟悉矩阵运算）（file:ble1）10.预测的评价指标注意，以下6个公式中的e表示的是预测误差，不是残差。可以在样本内、外预测。(1）预测误差。预测误差定义为e, = J,-y, 1=T+1, T+2, ..是对单点预测误差大小的测量。(2）相对误差PE(PercentageError)。-y,= T+1, T+2, ..PE=yt是对单点预测相对误差大小的测量。(3)误差均方根rmserror(RootMeanSquaredError)Z(,-y,)?rmserrorVTt=l通过若干个预测值对预测效果进行综合评价。5

= C Var( )C '= C σ 2 (X 'X ) -1C ' = σ 2 C (X 'X ) -1 β C ' , (1.33) ˆ 因为 服从多元正态分布，所以 β C 也是一个多元正态分布变量，即 ˆ β ˆ 1 ˆT + y = C ∼ N (Cβ, σ 2 C (X 'X ) -1 β C ') (1.34) ˆ 构成 t 分布统计量如下 t = ')'( ˆ ( ˆ ) 1 1 1 CXXC − + − + s yEyT T = ')'( ˆ 1 CXXC CC − − s ββ ∼ t (T-k) (1.35) 置信区间 C β ± tα/2 (1, T-k) s ˆ ')'( 1 CXXC − (1.36) (3) 单个 yT+1 的置信区间预测 yT+1 值与点预测值 有以下关系 1 ˆT + y yT+1 = + uT+1 (1.37) 1 ˆT + y 其中 uT+1 是随机误差项。因为 E( yT+1) = E( + uT+1) = Cβ (1.38) 1 ˆT + y Var( yT+1) = Var( ) + Var(uT+1) = σ 2 C (X 'X) -1C ' + σ 2 1 ˆT + y = σ 2 (C (X 'X) -1C ' + 1) (1.39) 因为 服从多元正态分布，所以 β yT+1也是一个多元正态分布变量，即 ˆ yT+1 ∼ N (Cβ, σ 2 C (X 'X ) -1C '+ 1) 与上相仿，单个 yT+1 的置信区间是 C β ± tα/2 (T-k) s ˆ 1')'( 1 + − CXXC (1.40) 计算举例：（见《计量经济分析》第 19-27 页，熟悉矩阵运算）（file:b1e1） 10. 预测的评价指标 注意，以下 6 个公式中的 et 表示的是预测误差，不是残差。可以在样本内、外预测。 (1) 预测误差。预测误差定义为 et = - yt, t = T+1, T+2, . t yˆ 是对单点预测误差大小的测量。 (2) 相对误差 PE (Percentage Error)。 PE = t tt y ˆ − yy , t = T+1, T+2, . 是对单点预测相对误差大小的测量。 (3) 误差均方根 rms error (Root Mean Squared Error) rms error = ∑= − T t tt yy T 1 2 ( ˆ ) 1 通过若干个预测值对预测效果进行综合评价。 5

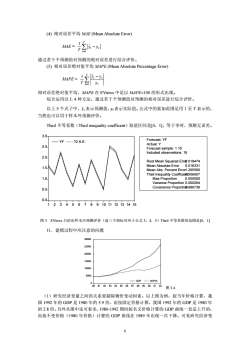
(4）绝对误差平均MAE（MeanAbsoluteError)-MAE=T2(=l通过若干个预测值对预测的绝对误差进行综合评价。(5）相对误差绝对值平均MAPE(MeanAbsolutePercentageError)1-yMAPE=相对误差绝对值平均，MAPE在EVieWs中是以MAPEx1O0的形式出现。综合运用以上4种方法，通过若干个预测值对预测的相对误差进行综合评价。以上5个式子中，表示预测值，V表示实际值。公式中的累加范围是用1至T表示的，当然也可以用于样本外预测评价。Theil不等系数（Theil inequalitycoefficent）取值区间是[O，1]，等于零时，预测无误差。3.0Forecast:YFYF.----?2S.E.Actual:Y2.5Forecastsample:115Includedobservations:152.0Root Mean Squared Err@.019474MeanAbsoluteError0.0163311.5MeanAbs.PercentErron.295560Theil Inequality Coefficieat0060071.0BiasProportion0.000000VarianceProportion0.000264Covariance Proportidin9997360.50.0123456789101112131415图3EViews只给出样本内预测评价（前三个指标对应于公式3，4，5）Theil不等系数的范围是[0，1]11.建模过程中应注意的问题30000250002000015000100005000GDPGDP(0)80818283848586878889909192图3.4（1）研究经济变量之间的关系要剔除物价变动因素。以上图为例，按当年价格计算，我国1992年的GDP是1980年的5.9倍，而按固定价格计算，我国1992年的GDP是1980年的2.8倍。另外从图中还可看出，1980-1992期间按名义价格计算的GDP曲线一直是上升的，而按不变价格（1980年价格）计算的GDP曲线在1989年出现一次下降。可见研究经济变6

(4) 绝对误差平均 MAE (Mean Absolute Error) MAE = ∑= − T t tt yy T 1 ˆ 1 通过若干个预测值对预测的绝对误差进行综合评价。 (5) 相对误差绝对值平均 MAPE (Mean Absolute Percentage Error) MAPE = ∑= − T t t tt y yy T 1 1 ˆ 相对误差绝对值平均，MAPE 在 EViews 中是以 MAPE×100 的形式出现。 综合运用以上 4 种方法，通过若干个预测值对预测的相对误差进行综合评价。 以上 5 个式子中， 表示预测值，yt 表示实际值。公式中的累加范围是用 1 至 T 表示的， 当然也可以用于样本外预测评价。 t yˆ Theil 不等系数（Theil inequality coefficent）取值区间是[0，1]，等于零时，预测无误差。 0.0 0.5 1.0 1.5 2.0 2.5 3.0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 YF ?2 S.E. Forecast: YF Actual: Y Forecast sample: 1 15 Included observations: 15 Root Mean Squared Error 0.019474 Mean Absolute Error 0.016331 Mean Abs. Percent Error 1.295560 Theil Inequality Coefficient 0.006007 Bias Proportion 0.000000 Variance Proportion 0.000264 Covariance Proportion 0.999736 图 3 EViews 只给出样本内预测评价（前三个指标对应于公式 3，4，5）Theil 不等系数的范围是[0，1] 11．建模过程中应注意的问题 0 5000 10000 15000 20000 25000 30000 80 81 82 83 84 85 86 87 88 89 90 91 92 GDP GDP(f) 图 3.4 （1）研究经济变量之间的关系要剔除物价变动因素。以上图为例，按当年价格计算，我 国 1992 年的 GDP 是 1980 年的 5.9 倍，而按固定价格计算，我国 1992 年的 GDP 是 1980 年 的 2.8 倍。另外从图中还可看出，1980-1992 期间按名义价格计算的 GDP 曲线一直是上升的， 而按不变价格（1980 年价格）计算的 GDP 曲线在 1989 年出现一次下降。可见研究经济变 6

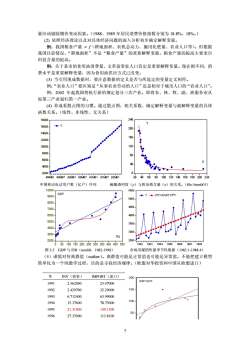
量应该剔除物价变动因素。（1988、1989年居民消费价格指数分别为18.8%、18%。）(2）依照经济理论以及对具体经济问题的深入分析初步确定解释变量。例：我国粮食产量=厂（耕地面积、农机总动力、施用化肥量、农业人口等）。但根据我国目前情况，“耕地面积”不是“粮食产量”的重要解释变量。粮食产量的提高主要来自科技含量的提高。例：关于某市的食用油消费量，文革前常驻人口肯定是重要解释变量。现在则不同，消费水平是重要解释变量，因为食用油供应方式已改变。(3）当引用现成数据时，要注意数据的定义是否与所选定的变量定义相符。例：“农业人口”要区别是“从事农业劳动的人口”还是相对于城市人口的“农业人口”。例：2002年起我国将执行新的规定划分三次产业。即将农、林、牧、副、渔服务业从原第三产业划归第一产业。（4）养成看散点图的习惯。通过散点图，相关系数，确定解释变量与被解释变量的具体函数关系。（线性、非线性、无关系）24018000YY160002001400016012000120100008000806000X4040000.200040608010012014016018020022099MD199MD7 00MD100MD701MD101MD702MD1205中国移动电话用户数（亿户）序列硫酸透明度（y）与铁杂质含量（x）的关系。（file:5nonlio1）100005500GDP2731.03+57.15*T90005000800045007000600400050003500400030003000FDI20000501001502002503003504004505001982198319841985198619871988图3.5GDP与FDI（nonli8，1982-1998）市场用煤销售量季节性数据（1982:1-1988:4）（5）谨慎对待离群值（outlier）。离群值可能是正常值也可能是异常值。不能把建立模型简单化为一个纯数学过程，目的是寻找经济规律。（欧盟对华投资和中国从欧盟进口）年INV（投资）IMPORT（进口）200IMPORT19912.56200023.4700015019922.42970032.2900019936.71240063.99000100199415.3760078.75000199521.31000149.130050199627.37000113.81007

量应该剔除物价变动因素。（1988、1989 年居民消费价格指数分别为 18.8%、18%。） (2) 依照经济理论以及对具体经济问题的深入分析初步确定解释变量。 例：我国粮食产量 = f（耕地面积、农机总动力、施用化肥量、农业人口等）。但根据 我国目前情况，“耕地面积”不是“粮食产量”的重要解释变量。粮食产量的提高主要来自 科技含量的提高。 例：关于某市的食用油消费量，文革前常驻人口肯定是重要解释变量。现在则不同，消 费水平是重要解释变量，因为食用油供应方式已改变。 (3) 当引用现成数据时，要注意数据的定义是否与所选定的变量定义相符。 例：“农业人口”要区别是“从事农业劳动的人口”还是相对于城市人口的“农业人口”。 例：2002 年起我国将执行新的规定划分三次产业。即将农、林、牧、副、渔服务业从 原第三产业划归第一产业。 (4) 养成看散点图的习惯。通过散点图，相关系数，确定解释变量与被解释变量的具体 函数关系。（线性、非线性、无关系） 中国移动电话用户数（亿户）序列 硫酸透明度（y）与铁杂质含量（x）的关系。（file:5nonli01） 图 3.5 GDP 与 FDI（nonli8，1982-1998） 市场用煤销售量季节性数据（1982:1-1988:4） （5）谨慎对待离群值（outlier）。离群值可能是正常值也可能是异常值。不能把建立模型 简单化为一个纯数学过程，目的是寻找经济规律。（欧盟对华投资和中国从欧盟进口） 年 INV（投资） IMPORT（进口） 1991 2.562000 23.47000 1992 2.429700 32.29000 1993 6.712400 63.99000 1994 15.37600 78.75000 1995 21.31000 149.1300 1996 27.37000 113.8100 7

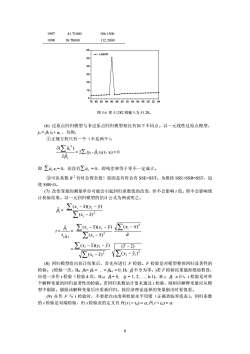
199741.71000106.1500199839.78000112.200060LABOR50 40.302010788082848688909294969800024图3.6把5.1282错输入为51.28。（6）过原点回归模型与非过原点回归模型相比有如下不同点。以一元线性过原点模型，y=x+u，为例，①正规方程只有一个（不是两个），a(Eu)=2Z (r-β,x) (-x)=0op,即Zi,x,=0，而没有Zi，=0，即残差和等于零不一定成立。②可决系数R?有时会得负值！原因是有时会有SSE>SST。为维持SSE+SSR=SST，迫使SSR1)=α,P(t<tα)=α8

1997 41.71000 106.1500 1998 39.78000 112.2000 0 10 20 30 40 50 60 78 80 82 84 86 88 90 92 94 96 98 00 02 04 LABOR 图 3.6 把 5.1282 错输入为 51.28。 (6) 过原点回归模型与非过原点回归模型相比有如下不同点。以一元线性过原点模型， yt = β1 xt + ut ，为例， ①正规方程只有一个（不是两个）， 1 2 ˆ ( ˆ ) ∂β ∂ ∑ut = 2∑ (yt - xt) (- xt) = 0 1 ˆ β 即 ∑uˆt xt = 0，而没有∑uˆt = 0，即残差和等于零不一定成立。 ②可决系数 R 2 有时会得负值！原因是有时会有 SSE>SST。为维持 SSE+SSR=SST，迫 使 SSR tα) = α, P( t < tα) = α 8

α/2a/2ad2Fa(k-1,T-k)-ta(Fk)ta(Fk)0图3.7图3.8（10）对于多元回归模型，当解释变量的量纲不相同时，不能在估计的回归系数之间比较大小。若要在多元回归模型中比较解释变量的相对重要性，应该对回归系数作如下变换s(xg)B,*=,(1.41)j= 1,2, ..., k-1s(y,)"其中s(x）和s(y）分别表示x和y的样本标准差。β，*可用来直接比较大小。以二元模型为例，标准化的回归模型表示如下（标准化后不存在截距项），-β++β+2-++s(y,)s(xa)s(x,2)两侧同乘s(y)，得(0%-j)= β* 50) ((-)+β*0(ae-2)+..+ u, SO)s(x,)s(x,2)因为均值点必在回归直线上，去掉上式中由均值点构成的方程，则必有=β*2+ β0xn+... +u,s(y)s(xa)s(x2)所以有s(Xg)B*S0)i= 1. 2.... k-1=β,i=1, 2, ..k-1, 即 β*=Ds(xy)s(y,)既是（1.41)式。（11）利用回归模型预测时，解释变量的值最好不要离开样本范围太远。原因是①根据预测公式离样本平均值越远，预测误差越大。以一元回归模型为例：~N(B+,(1++-)））TZ(x, -x)2从公式看，当xF=x时，的分布方差最小，即预测区间最小，预测精度最高。而预测点xF越远离，y的分布方差越大，即预测区间越大，预测精度越差。②有时，样本以外变量的关系不清楚。当样本外变量的关系与样本内变量的关系完全不同时，在样本外预测就会发生错误。图3.10给出青铜硬度与锡含量的关系曲线。若以锡含量为0-16%为样本，求得的关系近似是线性的。当把预测点选在锡含量为16%之外时，显然这种预测会发生严重错误。因为锡含量超过16%之后，青铜的硬度急剧下降，不再遵从锡含量为0-16%时的关系。9

图 3.7 图 3.8 (10) 对于多元回归模型，当解释变量的量纲不相同时，不能在估计的回归系数之间比 较大小。若要在多元回归模型中比较解释变量的相对重要性，应该对回归系数作如下变换 β j ˆ * = β j ˆ )( )( t tj ys xs , j = 1, 2, ., k-1 (1.41) 其中 s(xt) 和 s(yt) 分别表示 xt 和 yt 的样本标准差。 β ˆ j *可用来直接比较大小。 以二元模型为例，标准化的回归模型表示如下（标准化后不存在截距项）， )( t t ys − yy = β1* )( 1 11 t t xs − xx + β2* )( 2 22 t t xs − xx + . + ut 两侧同乘 s(yt)，得 (yt - y ) = β1* )( )( t1 t xs ys (xt1 - 1x ) + β2* )( )( t2 t xs ys (xt2 - 2 x ) + . + ut s(yt) 因为均值点必在回归直线上，去掉上式中由均值点构成的方程，则必有 yt = β1* )( )( t1 t xs ys xt1 + β2* )( )( t2 t xs ys xt2 + . + ut s(yt) 所以有 βj* )( )( tj t xs ys = βj, i = 1, 2, . k-1, 即 βj* = βj )( )( t tj ys xs , i = 1, 2, . k-1 既是 (1.41) 式。 (11) 利用回归模型预测时，解释变量的值最好不要离开样本范围太远。原因是①根据 预测公式离样本平均值越远，预测误差越大。以一元回归模型为例； F yˆ ∼ N (β0 + β1 xF, σ 2 (1+ T 1 + ∑ − − 2 2 )( )( xx xx t F ) ) 从公式看，当 xF = x 时， 的分布方差最小，即预测区间最小，预测精度最高。而预测点 xF越远离 F yˆ x ， 的分布方差越大，即预测区间越大，预测精度越差。 F yˆ ②有时，样本以外变量的关系不清楚。当样本外变量的关系与样本内变量的关系完全不 同时，在样本外预测就会发生错误。图 3.10 给出青铜硬度与锡含量的关系曲线。若以锡含 量为 0-16%为样本，求得的关系近似是线性的。当把预测点选在锡含量为 16%之外时，显然 这种预测会发生严重错误。因为锡含量超过 16%之后，青铜的硬度急剧下降，不再遵从锡 含量为 0-16%时的关系。 9

青铜硬度A16%锡含量（%）图3.9y的区间预测的变化图3.10青铜硬度与锡含量的关系青铜硬度16%锡含量（%）4c769(12）回归模型的估计结果应与经济理论或常识相一致。如边际消费倾向估计结果为1.5，则模型很难被接受。（产出对劳动力的弹性为负值！）（13）残差项应非自相关（用DW检验，亦可判断虚假回归）。否则说明①仍有重要解释变量被遗漏在模型之外。②选用的模型形式不妥。(14）通过对变量取对数消除异方差。(15）避免多重共线性。（16）解释变量应具有外生性，与误差项不相关。（17）应具有高度概括性。若模型的各种检验及预测能力大致相同，应选择解释变量较少的一个。（18）模型的结构稳定性要强，超样本特性要好。（19）世界是变化的，应该随时间的推移及时修改模型。建模案例1：《全国味精需求量的计量经济模型》（file:1c02）（见《预测》1987年第2期）1，依据经济理论选择影响味精需求量变化的因素依据经济理论一种商品的需求量主要取决于四个因素，即①商品价格，②代用品价格，③消费者收入水平，④消费者偏好。模型为：商品需求量=f（商品价格，代用品价格，收入水平，消费者偏好）对于特定商品味精，当建立模型时要对上述四个因素能否作为重要解释变量逐一鉴别商品价格：味精是一种生活常用品，当时又是一种价格较高的调味品。初步判断价格会对需求量产生影响。所以确定价格作为一个重要解释变量。代用品价格：味精是一种独特的调味品，目前尚没有替代商品。所以不考虑代用品价格这一因素。消费者收入：显然消费者收入应该是一个较重要的解释变量。偏好：由于因偏好不食味精或大量食用味精的情形很少见，所以每人用量只会在小范围内波动，所以不把偏好作为重要解释变量，而归并入随机误差项。分析结果，针对味精需求量只考虑两个重要解释变量，商品价格和消费者收入水平。味精需求量=（商品价格，收入水平）2．选择恰当的变量（既要考虑代表性，也要考虑可能性）10

图 3.9 yt 的区间预测的变化 图 3.10 青铜硬度与锡含量的关系 4 6 8 10 12 55 60 65 70 75 80 85 90 95 LOG(TRADE) (12) 回归模型的估计结果应与经济理论或常识相一致。如边际消费倾向估计结果为1.5， 则模型很难被接受。（产出对劳动力的弹性为负值！） (13) 残差项应非自相关（用 DW 检验，亦可判断虚假回归）。否则说明①仍有重要解释 变量被遗漏在模型之外。②选用的模型形式不妥。 (14) 通过对变量取对数消除异方差。 (15) 避免多重共线性。 (16) 解释变量应具有外生性，与误差项不相关。 (17) 应具有高度概括性。若模型的各种检验及预测能力大致相同，应选择解释变量较 少的一个。 (18) 模型的结构稳定性要强，超样本特性要好。 (19) 世界是变化的，应该随时间的推移及时修改模型。 建模案例 1：《全国味精需求量的计量经济模型》（file:1c02） （见《预测》1987 年第 2 期） 1．依据经济理论选择影响味精需求量变化的因素 依据经济理论一种商品的需求量主要取决于四个因素，即①商品价格，②代用品价格， ③消费者收入水平，④消费者偏好。模型为： 商品需求量 = f (商品价格，代用品价格，收入水平，消费者偏好) 对于特定商品味精，当建立模型时要对上述四个因素能否作为重要解释变量逐一鉴别。 商品价格：味精是一种生活常用品，当时又是一种价格较高的调味品。初步判断价格会 对需求量产生影响。所以确定价格作为一个重要解释变量。 代用品价格：味精是一种独特的调味品，目前尚没有替代商品。所以不考虑代用品价格 这一因素。 消费者收入：显然消费者收入应该是一个较重要的解释变量。 偏好：由于因偏好不食味精或大量食用味精的情形很少见，所以每人用量只会在小范围 内波动，所以不把偏好作为重要解释变量，而归并入随机误差项。 分析结果，针对味精需求量只考虑两个重要解释变量，商品价格和消费者收入水平。 味精需求量 = f (商品价格，收入水平) 2．选择恰当的变量（既要考虑代表性，也要考虑可能性） 10