《计量经济学》课程授课教案（讲稿）10 时间序列模型

第2章时间序列模型时间序列分析方法由Box-Jenkins(1976）年提出。它适用于各种领域的时间序列分析。时间序列模型不同于经济计量模型的两个特点是：（1）这种建模方法不以经济理论为依据，而是依据变量自身的变化规律，利用外推机制描述时间序列的变化。(2）明确考患时间序列的非平稳性。如果时间序列非平稳，建立模型之前应先通过差分把它变换成平稳的时间序列，再考虑建模问题。时间序列模型的应用：（1）研究时间序列本身的变化规律（何种结构，建立模型，有无确定性趋势，有无单位根，有无季节性成分）。（2）在回归模型的预测中首先预测解释变量的值。（3）非经典经济计量学是回归模型知识与时间序列模型知识的结合。1.随机过程、时间序列定义2.时间序列（ARIMA）模型的分类3.自相关函数与偏自相关函数4：建模步骤（识别、参数估计、诊断检验、预测）5.ARIMA模型案例分析与预测6.季节时间序列（SARIMA）模型7.SARIMA模型案例分析与预测8.回归与时间序列组合模型分析与预测9.时间序列模型干扰分析2.1随机过程、时间序列定义为什么在研究时间序列之前先要介绍随机过程？就是要把时间序列的研究提高到理论高度来认识。时间序列不是无源之水。它是由相应随机过程产生的。只有从随机过程的高度认识了它的一般规律。对时间序列的研究才会有指导意义。对时间序列的认识才会更深刻。自然界中事物变化的过程可以分成两类。一类是确定型过程，一类是非确定型过程。确定型过程即可以用关于时间1的函数描述的过程。例如，真空中的自由落体运动过程，电容器通过电阻的放电过程，行星的运动过程等。非确定型过程即不能用一个（或几个）关于时间t的确定性函数描述的过程。换句话说，对同一事物的变化过程独立、重复地进行多次观测而得到的结果是不相同的。例如，对河流水位的测量。其中每一时刻的水位值都是一个随机变量。如果以一年的水位纪录作为实验结果，便得到一个水位关于时间的函数x，。这个水位函数是预先不可确知的。只有通过测量才能得到。而在每年中同一时刻的水位纪录是不相同的。随机过程：由随机变量组成的一个有序序列称为随机过程，记为(x(s,1)，seS,teT)。其中S表示样本空间，T表示序数集。对于每一个t,teT，x（）是样本空间S中的一个随机变量。对于每一个s,seS,x(s，）是随机过程在序数集T中的一次实现。，x.,x)., x.1,x)(x12,x2随机过程..样本空间(xr))XT-1,TX2,1

第 2 章 时间序列模型 时间序列分析方法由 Box-Jenkins (1976) 年提出。它适用于各种领域的时间序列分析。 时间序列模型不同于经济计量模型的两个特点是： ⑴ 这种建模方法不以经济理论为依据，而是依据变量自身的变化规律，利用外推机制 描述时间序列的变化。 ⑵ 明确考虑时间序列的非平稳性。如果时间序列非平稳，建立模型之前应先通过差分 把它变换成平稳的时间序列，再考虑建模问题。 时间序列模型的应用： （1）研究时间序列本身的变化规律（何种结构，建立模型，有无确定性趋势，有无单 位根，有无季节性成分）。 （2）在回归模型的预测中首先预测解释变量的值。 （3）非经典经济计量学是回归模型知识与时间序列模型知识的结合。 1．随机过程、时间序列定义 2．时间序列（ARIMA）模型的分类 3．自相关函数与偏自相关函数 4．建模步骤（识别、参数估计、诊断检验、预测） 5．ARIMA 模型案例分析与预测 6．季节时间序列（SARIMA）模型 7．SARIMA 模型案例分析与预测 8．回归与时间序列组合模型分析与预测 9．时间序列模型干扰分析 2.1 随机过程、时间序列定义 为什么在研究时间序列之前先要介绍随机过程？就是要把时间序列的研究提高到理论 高度来认识。时间序列不是无源之水。它是由相应随机过程产生的。只有从随机过程的高度 认识了它的一般规律。对时间序列的研究才会有指导意义。对时间序列的认识才会更深刻。 自然界中事物变化的过程可以分成两类。一类是确定型过程，一类是非确定型过程。 确定型过程即可以用关于时间 t 的函数描述的过程。例如，真空中的自由落体运动过程， 电容器通过电阻的放电过程，行星的运动过程等。 非确定型过程即不能用一个（或几个）关于时间 t 的确定性函数描述的过程。换句话说， 对同一事物的变化过程独立、重复地进行多次观测而得到的结果是不相同的。例如，对河流 水位的测量。其中每一时刻的水位值都是一个随机变量。如果以一年的水位纪录作为实验结 果，便得到一个水位关于时间的函数 xt。这个水位函数是预先不可确知的。只有通过测量才 能得到。而在每年中同一时刻的水位纪录是不相同的。 随机过程：由随机变量组成的一个有序序列称为随机过程，记为{x (s, t) , s∈S , t∈T }。 其中 S 表示样本空间，T 表示序数集。对于每一个 t, t∈T, x (·, t ) 是样本空间 S 中的一个随 机变量。对于每一个 s, s∈S , x (s, ·) 是随机过程在序数集 T 中的一次实现。 {x1 1 , x2 1 , ., xT-1 1 , xT 1 } {x1 2 , x2 2 , ., xT-1 2 , xT 2 } 随机过程 : : : : : {x1 s , x2 s , ., xT-1 s , xT s } 样本空间 1

随机过程简记为（x）或xt。随机过程也常简称为过程。随机过程一般分为两类。一类是离散型的，一类是连续型的。如果一个随机过程(x)对任意的teT都是一个连续型随机变量，则称此随机过程为连续型随机过程。如果一个随机过程x对任意的teT都是一个离散型随机变量，则称此随机过程为离散型随机过程。本书只考虑离散型随机过程。一连续型（严（强）平稳过程随机过程平稳的人L宽平稳过程离散型非平稳的严（强）平稳过程：一个随机过程中若随机变量的任意子集的联合分布函数与时间无关，即无论对T的任何时间子集（1,2…,,）以及任何实数k,(t+k)eT,i=1,2,.,n都有F(x(t1), x(t2), .-, x(tn) ) = F(x(tI + k), x(t2+ k), .. , x(tn + k))成立，其中F）表示n个随机变量的联合分布函数，则称其为严平稳过程或强平稳过程。严平稳意味着随机过程所有存在的矩都不随时间的变化而变化。严平稳的条件是非常严格的，而且对于一个随机过程，上述联合分布函数不便于分析和使用。因此希望给出不象强平稳那样严格的条件。若放松条件，则可以只要求分布的主要参数相同。如只要求从一阶到某阶的矩函数相同。这就引出了宽平稳概念，如果一个随机过程m阶矩以下的矩的取值全部与时间无关，则称该过程为m阶平稳过程。比如E[x(t) ] = E[x(t; + k)] = μ< 00,Var[x(t)] = Var[x(t; + k)] = ? <00,Cov[x(t), x(t)] = Cov[x (t; + k), x (t, + k)] = if <00,其中μ,2和α为常数，不随t,(teT);k,（(t+k)T,r=ij）变化而变化，则称该随机过程（x）为二阶平稳过程（协方差平稳过程）。该过程属于宽平稳过程。如果严平稳过程的二阶矩为有限常数值，则其一定是宽平稳过程。反之，一个宽平稳过程不一定是严平稳过程。但对于正态随机过程而言，严平稳与宽平稳是一致的。这是因为正态随机过程的联合分布函数完全由均值、方差和协方差所惟一确定。本书简称二阶平稳过程为平稳过程。时间序列：随机过程的一次实现称为时间序列，也用(x，）或x，表示。与随机过程相对应，时间序列分类如下，连续型*（心电图，水位纪录仪，温度纪录仪）C时间序列从相同的时间间隔点上取自连续变化的序列（人口序列）离散型3一定时间间隔内的累集值（年粮食产量，进出口额序列）时间序列中的元素称为观测值。(x既表示随机过程，也表示时间序列。x既表示随机过程的元素随即变量，也表示时间序列的元素观测值。在不致引起混淆的情况下，为方便，x也直接表示随机过程和时间序列。随机过程与时间序列的关系如下所示：2

随机过程简记为 {xt} 或 xt。随机过程也常简称为过程。 随机过程一般分为两类。一类是离散型的，一类是连续型的。如果一个随机过程{xt}对 任意的 t∈T 都是一个连续型随机变量，则称此随机过程为连续型随机过程。如果一个随机 过程{xt}对任意的 t∈T 都是一个离散型随机变量，则称此随机过程为离散型随机过程。本书 只考虑离散型随机过程。 连续型 严（强）平稳过程 随机过程 平稳的 离散型 宽平稳过程 非平稳的 严（强）平稳过程：一个随机过程中若随机变量的任意子集的联合分布函数与时间无关， 即无论对 T 的任何时间子集（t1, t 2, ., tn）以及任何实数 k, (ti + k) ∈T, i = 1, 2, ., n 都有 F( x(t1), x(t2), ., x(tn) ) = F(x(t1 + k), x(t2 + k), . , x(tn + k) ) 成立，其中 F(·) 表示 n 个随机变量的联合分布函数，则称其为严平稳过程或强平稳过程。 严平稳意味着随机过程所有存在的矩都不随时间的变化而变化。严平稳的条件是非常严 格的，而且对于一个随机过程，上述联合分布函数不便于分析和使用。因此希望给出不象强 平稳那样严格的条件。若放松条件，则可以只要求分布的主要参数相同。如只要求从一阶到 某阶的矩函数相同。这就引出了宽平稳概念。 如果一个随机过程 m 阶矩以下的矩的取值全部与时间无关，则称该过程为 m 阶平稳过 程。比如 E[ x(ti) ] = E[ x(ti + k)] = μ < ∞, Var[x(ti)] = Var[x(ti + k)] = σ 2 < ∞, Cov[x(ti), x(tj)] = Cov[x (ti + k), x (tj + k)] = σ i j 2 < ∞, 其中 μ , σ 2 和 σ ij 2 为常数，不随 t, (t∈T ); k, ( (tr + k) ∈T, r = i, j ) 变化而变化，则称该随 机过程 {xt} 为二阶平稳过程（协方差平稳过程）。该过程属于宽平稳过程。 如果严平稳过程的二阶矩为有限常数值，则其一定是宽平稳过程。反之，一个宽平稳过 程不一定是严平稳过程。但对于正态随机过程而言，严平稳与宽平稳是一致的。这是因为正 态随机过程的联合分布函数完全由均值、方差和协方差所惟一确定。本书简称二阶平稳过程 为平稳过程。 时间序列：随机过程的一次实现称为时间序列，也用{x t }或 x t 表示。 与随机过程相对应，时间序列分类如下， 连续型* （心电图，水位纪录仪，温度纪录仪） 时间序列 从相同的时间间隔点上取自连续变化的序列（人口序列） 离散型 一定时间间隔内的累集值（年粮食产量，进出口额序列） 时间序列中的元素称为观测值。{xt}既表示随机过程，也表示时间序列。xt 既表示随机 过程的元素随即变量，也表示时间序列的元素观测值。在不致引起混淆的情况下，为方便， xt 也直接表示随机过程和时间序列。 随机过程与时间序列的关系如下所示： 2

随机过程：(x1,X2, .*,XT-1,XT,)第1次观测：(x，x2,.,x., x)第2次观测：(xz，x2,，.. XT-, XT)：：：：第n次观测：(x"，x2"，..xr-"，x)某河流一年的水位值，(xX1,x2，…，xT-1,xT,)，可以看作一个随机过程。每一年的水位纪录则是一个时间序列，(xl,x2，.,xT-,xT)。而在每年中同一时刻（如t=2时）的水位纪录是不相同的。（x2,x2，x2"）构成了x2取值的样本空间。例如，要记录某市日电力消耗量，则每日的电力消耗量就是一个随机变量，于是得到一个日电力消耗量关于天数t的函数。而这些以年为单位的函数族构成了一个随机过程(x)，1=1,2..365。因为时间以天为单位，是离散的，所以这个随机过程是离散型随机过程。而一年的日电力消耗量的实际观测值序列就是一个时间序列。自然科学领域中的许多时间序列常常是平稳的。如工业生产中对液面、压力、温度的控制过程，某地的气温变化过程，某地100年的水文资料，单位时间内路口通过的车辆数过程等。但经济领域中多数宏观经济时间序列却都是非平稳的。如一个国家的年GDP序列，年投资序列，年进出口序列等。为便于计算，先给出差分、差分算子、滞后算子定义。差分：时间序列变量的本期值与其滞后值相减的运算叫差分。差分分为一阶差分和高阶差分。首先给出差分符号。对于时间序列x，，一阶差分可表示为(2.1)X-XI-1 = △ x, = (1- L) x,= X,- Lx)其中4称为一阶差分算子（也用D表示）。L称为滞后算子（也用B表示），其定义是L"x,=Xt-n o差分算子和滞后算子可以直接参与运算。二次一阶差分表示为，x,= 4 x, - 4X-I = (x,-X1-1) -(Xi-1 - XI-2) =X, - 2 Xf-I+ X(-2,或x, =(1- L)2 x,=(1 - 2L + L3) x,= x;-2 x-I+ xμ2(2.2)k阶差分可表示为X1-XI-= 4k X,=(1- L*)x,= X- L* xk阶差分常用于季节性数据的差分，如4阶差分、12阶差分。滞后算子有如下性质。（1）常数与滞后算子相乘等于常数。Lc=C（2）滞后算子适用于分配率。（L+L)x=L'x+x=Xr-+Xi-（3）滞后算子适用于结合率。L'x=L+/x,=X-j()x,=L2/x=X-2)（4）滞后算子的零次方等于1。L°x=x（5）滞后算子的负整数次方意味着超前。L"x,=x3

随机过程: {x1, x2, ., xT-1, xT,} 第 1 次观测：{x1 1 , x2 1 , ., xT-1 1 , xT 1 } 第 2 次观测：{x1 2 , x2 2 , ., xT-1 2 , xT 2 } : : : : : 第 n 次观测：{x1 n , x2 n , ., xT-1 n , xT n } 某河流一年的水位值，{x1, x2, ., xT-1, xT,}，可以看作一个随机过程。每一年的水位纪录 则是一个时间序列，{x1 1 , x2 1 , ., xT-1 1 , xT 1 }。而在每年中同一时刻（如 t = 2 时）的水位纪录 是不相同的。{ x2 1 , x2 2 , ., x2 n ,} 构成了 x2 取值的样本空间。 例如，要记录某市日电力消耗量，则每日的电力消耗量就是一个随机变量，于是得到一 个日电力消耗量关于天数 t 的函数。而这些以年为单位的函数族构成了一个随机过程 {xt}, t = 1, 2, . 365。因为时间以天为单位，是离散的，所以这个随机过程是离散型随机过程。而 一年的日电力消耗量的实际观测值序列就是一个时间序列。 自然科学领域中的许多时间序列常常是平稳的。如工业生产中对液面、压力、温度的控 制过程，某地的气温变化过程，某地 100 年的水文资料，单位时间内路口通过的车辆数过程 等。但经济领域中多数宏观经济时间序列却都是非平稳的。如一个国家的年 GDP 序列，年 投资序列，年进出口序列等。 为便于计算，先给出差分、差分算子、滞后算子定义。 差分：时间序列变量的本期值与其滞后值相减的运算叫差分。差分分为一阶差分和高阶 差分。 首先给出差分符号。对于时间序列 x t ，一阶差分可表示为 xt - xt -1 = Δ xt = (1- L) xt = xt - L xt (2.1) 其中Δ 称为一阶差分算子（也用 D 表示）。L 称为滞后算子（也用 B 表示），其定义是 Ln xt = xt- n 。 差分算子和滞后算子可以直接参与运算。 二次一阶差分表示为， Δ 2 xt = Δ xt - Δ xt -1 = (xt - xt -1) – (xt-1 - xt -2) = xt - 2 xt -1+ xt –2， 或 Δ 2 xt = (1- L ) 2 xt = (1 – 2L + L 2 ) xt = xt –2 xt-1+ xt–2 (2.2) k 阶差分可表示为 xt - xt -k = Δk xt = (1- Lk ) xt = xt – Lk xt k 阶差分常用于季节性数据的差分，如 4 阶差分、12 阶差分。 滞后算子有如下性质。 （1）常数与滞后算子相乘等于常数。Lc = c （2）滞后算子适用于分配率。(Li + Lj ) xt = Li xt + Lj xt = xt -i+ xt –j （3）滞后算子适用于结合率。Li Lj xt = Li+ j xt = xt -i–j, (Lj ) 2 xt = L2 j xt = xt–2 j （4）滞后算子的零次方等于 1。L0 xt = xt （5）滞后算子的负整数次方意味着超前。L-i xt = xt+i 3

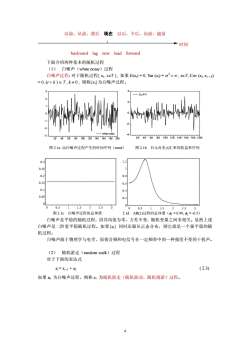
以前，从前，滞后现在以后，今后，向前，超前时间backwardlagnowleadforward下面介绍两种基本的随机过程（1）白噪声（whitenoise）过程白噪声过程：对于随机过程(xt,teT)，如果E(x)=0,Var(x)=α<00,teT,Cov(x,x+k)=0,(t+k）eT,k+0，则称(x)为白噪声过程。20406080100120140160180200406080100120140160180200图2.1a由白噪声过程产生的时间序列（nrnd）图2.1b日元对美元汇率的收益率序列0.30.250.2[0.150.10.0.05.oF0.51.522.500.501.522.5图2.1c白噪声过程的总体谱2.1dAR(2)过程的总体谱（=0.99,更=-0.5)白噪声是平稳的随机过程，因其均值为零，方差不变，随机变量之间非相关。显然上述白噪声是二阶宽平稳随机过程。如果x同时还服从正态分布，则它就是一个强平稳的随机过程。白噪声源于物理学与电学，原指音频和电信号在一定频带中的一种强度不变的干扰声。(2)随机游走（randomwalk）过程对于下面的表达式(2.3)X,=Xr-1 + ut如果u为白噪声过程，则称x，为随机游走（随机游动、随机漫游）过程。A

以前，从前，滞后 现在 以后，今后，向前，超前 时间 backward lag now lead forward 下面介绍两种基本的随机过程 （1） 白噪声（white noise）过程 白噪声过程：对于随机过程{ xt , t∈T }, 如果 E(xt) = 0, Var (xt) = σ 2 < ∞ , t∈T; Cov (xt, xt + k) = 0, (t + k ) ∈ T , k ≠ 0 , 则称{xt}为白噪声过程。 -3 -2 -1 0 1 2 3 20 40 60 80 100 120 140 160 180 200 white noise -4 -2 0 2 4 20 40 60 80 100 120 140 160 180 200 DJPY 图 2.1a 由白噪声过程产生的时间序列（nrnd） 图 2.1b 日元对美元汇率的收益率序列 0 0.5 1 1.5 2 2.5 3 0 0.05 0.1 0.15 0.2 0.25 0.3 0 0.5 1 1.5 2 2.5 3 0 0.2 0.4 0.6 0.8 1 1.2 图 2.1c 白噪声过程的总体谱 2.1d AR(2)过程的总体谱（φ1 = 0.99, φ2 = -0.5） 白噪声是平稳的随机过程，因其均值为零，方差不变，随机变量之间非相关。显然上述 白噪声是二阶宽平稳随机过程。如果{xt} 同时还服从正态分布，则它就是一个强平稳的随 机过程。 白噪声源于物理学与电学，原指音频和电信号在一定频带中的一种强度不变的干扰声。 （2） 随机游走（random walk）过程 对于下面的表达式 xt = xt -1 + ut ( 2.3) 如果 ut 为白噪声过程，则称 xt 为随机游走（随机游动、随机漫游）过程。 4

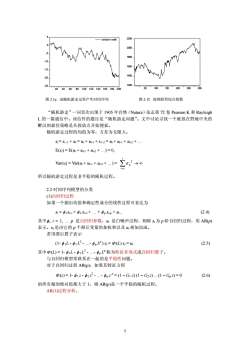
-10-15-202F1502503010020020406080100120140160180200图2.1e.由随机游走过程产生时间序列图2.1f.深圳股票综合指数“随机游走”一词首次出现于1905年自然（Nature）杂志第72卷PearsonK.和RayleighL.的一篇通信中。该信件的题目是“随机游走问题”。文中讨论寻找一个被放在野地中央的醉汉的最佳策略是从投放点开始搜索。随机游走过程的均值为零，方差为无限大。X,=Xr-I +ut=ur+u-I +Xr-2=u, +u-I +u-2+...E(x)=E(u, + uri +u-2 +...)=0,Var(x.)= Var(u, + u-I + u-2 + ...) =:dG所以随机游走过程是非平稳的随机过程。2.2时间序列模型的分类(1)自回归过程如果一个剔出均值和确定性成分的线性过程可表达为(2.4)X,=Φix-1+Φ2X-2+....+Φpxi-p+ut,其中，i=1，p是自回归参数，u是白噪声过程，则称x为p阶自回归过程，用ARp)表示。x是由它的p个滞后变量的加权和以及u相加而成。若用滞后算子表示(1-Φ-Φ2L-.-ΦpLP)x,=(L)x,=ut(2.5)其中@(L)=1-ΦL-2L?--更,LP称为特征多项式或自回归算子。与自回归模型常联系在一起的是平稳性问题。对于自回归过程AR(p)，如果其特征方程@()=1-Φ1=- Φ222-..-Φp=P=(1-G12)(1-G2=)..(1-Gp=)=0(2.6)的所有根的绝对值都大于1，则AR(p)是一个平稳的随机过程。AR(1)过程分析。5

-25 -20 -15 -10 -5 0 5 20 40 60 80 100 120 140 160 180 200 random walk 1200 1400 1600 1800 2000 2200 50 100 150 200 250 300 图 2.1e. 由随机游走过程产生时间序列 图 2.1f. 深圳股票综合指数 游走问题”。文中讨论寻找一个被放在野地中央的 醉汉 ut-1 + ut-2 + . E(xt) = E(ut + ut-1 + ut-2 + .) = 0, Var(xt) = Var(ut + ut-1 + ut-2 + .) = → ∞ 以随机游走过程是非平稳的随机过程。 的分类 t为 p 阶自回归过程，用 AR(p) 后变量的加权和以及 ut相加而成。 2 p (2.5) 其中 或自回归算子。 。 ) 2 p – Gp z) = 0 (2.6) 的所有根的绝对值都大于 1，则 AR(p)是一个平稳的随机过程。 AR(1)过程分析。 “随机游走”一词首次出现于 1905 年自然（Nature）杂志第 72 卷 Pearson K.和 Rayleigh L.的一篇通信中。该信件的题目是“随机 的最佳策略是从投放点开始搜索。 随机游走过程的均值为零，方差为无限大。 xt = xt -1 + ut = ut + ut-1 + xt -2 = ut + ∑∞− t u 2 σ 所 2.2 时间序列模型 (1)自回归过程 如果一个剔出均值和确定性成分的线性过程可表达为 xt = φ 1xt-1 + φ 2 xt-2 + . + φ p xt-p + ut , (2.4) 其中φi, i = 1, . p 是自回归参数，ut 是白噪声过程，则称 x 表示。xt 是由它的 p 个滞 若用滞后算子表示 (1- φ 1L - φ 2 L - .- φ p L ) xt = Φ (L) xt = ut Φ (L) = 1- φ 1L - φ 2 L2 - .- φ p Lp 称为特征多项式 与自回归模型常联系在一起的是平稳性问题 对于自回归过程 AR(p ，如果其特征方程 Φ (z) = 1- φ 1 z - φ 2 z - .- φ p z = (1 – G1 z) (1 – G2 z) . (1 5

20406080100120140160180200图2.2AR(1)过程(2.7)X=0ix-I+ut保持其平稳性的条件是特征方程(1 - $L)=0根的绝对值必须大于1，满足[1/ 6i/>1也就是I ]<1解释如下：一阶自回归过程，x,=1xi-1+ut，可写为(1- L) x, = ux,= (1- , L)" u,在「<1条件下，有X=(1+ ΦL+(L)2+ ( L) 3 +.) ut若保证AR(1)具有平稳性，Z必须收敛，即必须满足|<1。这是容易理解的，如果|i≥l，i发散，于是x变成一个非平稳随机过程。由（2.7）式有X,= u,+ ur-1 + gf x12= u + u.+ + g? up2 +...（短记忆过程）因为u是一个白噪声过程，所以对于平稳的AR(1)过程E(x) = 0Var (x)= o,? + ? o,2+ o, +..=.1-d,2上式也说明若保证x平稳，必须保证「则<1。例1：有AR(1)模型则，（1-0.6L)x=urX=0.6x-1+u1u,=(1 +0.6 L+0.36 L2+ 0.216 L +..) u,X,=1-0.6L= u, +0.6 ut-i +0.36 u-2 +0.216 u-3+.6

-4 -2 0 2 4 20 40 60 80 100 120 140 160 180 200 AR(1) 图 2.2 AR(1)过程 xt = φ 1 xt-1+ ut (2.7) 保持其平稳性的条件是特征方程 (1 - φ 1 L) = 0 根的绝对值必须大于 1，满足 |1/φ1|> 1 也就是 | φ1| < 1 解释如下：一阶自回归过程，xt = φ 1 xt-1+ ut，可写为 (1- φ1L) xt = ut xt = (1- φ1 L) -1 ut 在 | φ1| < 1 条件下，有 xt = (1+ φ1L + (φ1 L) 2 + (φ1 L) 3 +.) ut 若保证 AR(1)具有平稳性， 必须收敛，即φ1 必须满足|φ1|< 1。这是容易理解的， 如果|φ1|≥1， 发散，于是 xt 变成一个非平稳随机过程。 ∑∞ =0i 1 i i φ L ∑∞ =0i 1 i i φ L 由（2.7）式有 xt = ut + φ1 ut-1 + φ1 2 xt-2 = ut + φ1 ut-1 + φ1 2 ut-2 +. （短记忆过程） 因为 ut 是一个白噪声过程，所以对于平稳的 AR(1)过程 E(xt) = 0 Var (xt) = σu 2 + φ1 2 σu 2 + φ1 4 σu 2 +. = 2 2 1 1 1 σ u −φ 上式也说明若保证 xt 平稳，必须保证 | φ1| < 1。 例 1：有 AR(1) 模型 xt = 0.6 x t-1 + ut 则，(1 - 0.6 L ) x t = ut xt = 6.01 L 1 − ut = (1 + 0.6 L + 0.36 L2 + 0.216 L3 + . ) ut = ut + 0.6 ut-1 + 0.36 ut-2 + 0.216 ut-3 + . 6

上式变换为一个无限阶的移动平均过程。AR(2)过程分析。(0)X=01X-1+02X-2+u具有平稳性的条件。对于AR(2）过程，特征方程式是1--2=0上式的两个根是L, L2= 9±V0°+4g202设入=1/L，则相应的特征方程是。-0-2=0其两个根是1,=+/0+402(1)2根,分别与Li,Lz互为倒数关系。那么AR(2）模型具有平稳性的条件是ILil>1,ILI>1（在单位圆外）或(2)[0，从而得(5)Φ2+$,<1(6)单2-Φ/<1由(2)和(4)式得-1<@2<1(7)(5)，（6)和（7）式是保证AR(2）过程平稳，回归参数Φ2，所应具有的条件。若(5)、(6)和（7)式成立，则特征方程1-Φ,L-Φ2L=0的根必在单位圆之外。条件(5)，（6)和（7)给出的区域称为平稳域。是一个三角形区域。见下图阴影部分。7

上式变换为一个无限阶的移动平均过程。 AR(2)过程分析。 xt = φ 1 xt-1+φ 2 xt-2+ ut (0) 具有平稳性的条件。 对于 AR(2) 过程，特征方程式是 1 - φ 1 L - φ 2 L2 = 0 上式的两个根是 L1, L2 = 2 2 2 11 2 4 φ φφφ − +± 设λ = 1 / L，则相应的特征方程是。 λ 2 - φ 1 λ - φ 2 = 0 其两个根是 λ1, λ2 = 2 4 2 2 ∓ 11 + φφφ (1) 根λ1, λ2 分别与 L1, L2 互为倒数关系。那么 AR(2) 模型具有平稳性的条件是 | L1| > 1, | L2| > 1 （在单位圆外）或 | λ1| 0，从而得 φ 2 + φ 1 < 1 (5) φ 2 - φ 1 < 1 (6) 由 (2) 和 (4) 式得 -1 < φ 2 < 1 (7) (5)，(6)和 (7) 式是保证 AR(2) 过程平稳，回归参数φ 2, φ 1 所应具有的条件。若(5)、(6)和 (7) 式成立，则特征方程 1- φ 1 L - φ 2 L = 0 的根必在单位圆之外。条件 (5)，(6)和 (7)给出的区域 称为平稳域。是一个三角形区域。见下图阴影部分。 7

92+q=1Φ2-0=1过阻尼=122-291少2=-1-1次阻尼临界阻尼9?+4g2=0图1平稳AR(2）过程，取值域（阴影部分）回归参数2，，的取值变化分三种情形讨论。（1）当2+4$2=0时，有L=L为相等实数根。，，取值在图中的抛物线上，称为临界阻尼状态。(2）当+4$2>0时，L1，L2为不等实数根。，的值位于过阻尼区（自相关函数呈指数衰减）。(3)当+42<0时，根为共轭复根。Φ2，Φ的值位于欠阻尼区（自相关函数呈正弦震荡衰减）。例2有AR(2)模型x,=0.7x-1-0.1x-2+u，试判别x,的平稳性。解：有3种方法。解法1：（检查，约束条件）+=0.6，-+Φ=-0.8，=-0.1，满足条件（5）（6）（7），所以x是平稳的。解法2：（因式分解求根）由原式得（1-0.7L+0.1L2）x,=u。特征方程为，(1 - 0.7 L+ 0.1 L2)=0(1 - 0.2 L)(1- 0.5 L)= 0特征方程的两个根是，L,=5，L,=2。因为两个根都在单位圆之外，所以x是平稳的。解法3：（观察（，）点是否落在三角区）从图1看，因为（，）=(0.7,-0.1)，落在了AR(2)过程的平稳域，落在了过阻尼区，所以x,为平稳过程。例3：有AR(2）模型x,=0.6x-1-0.1xt-2+ut，试判别x的平稳性。解：解法1：（检查，$约束条件）+,=0.5，-年+，=-0.7，=-0.1，满足条件（5）（6）（7)，所以x,是平稳的。因为特征方程中各项都是实数，所以其虚根必然是共轭的。[1- (0.3 - 0.1i) L] [1- (0.3 + 0.17) L]= 0特征方程的两个根是，1(0.3 + 0.1i)Li ==3 +i,0.3-0.1i(0.30.1/)(0.3 +0.1)1L2==3-i,0.3+0.1i8

图 1 平稳 AR(2) 过程φ1, φ2取值域（阴影部分） 回归参数φ 2，φ 1 的取值变化分三种情形讨论。（1）当φ 1 2 + 4φ 2 = 0 时，有 L1 = L2 为相 等实数根。φ2, φ 1 取值在图中的抛物线上，称为临界阻尼状态。(2) 当 φ 1 2 + 4φ 2 > 0 时，L1, L2 为不等实数根。φ2, φ1 的值位于过阻尼区（自相关函数呈指数衰减）。(3)当 φ 1 2 + 4φ 2 < 0 时，根为共轭复根。φ 2, φ 1 的值位于欠阻尼区（自相关函数呈正弦震荡衰减）。 例 2 有 AR(2) 模型 xt = 0.7 xt -1 - 0.1 xt -2 + ut，试判别 xt 的平稳性。 解：有 3 种方法。 解法 1：（检查φ1, φ2 约束条件） 1 ˆ φ + = 0.6，- + = -0.8， = - 0.1，满足条件（5）（6）（7），所以 xt 是平稳的。 2 ˆ φ 1 ˆ φ 2 ˆ φ 2 ˆ φ 解法 2：（因式分解求根） 由原式得 (1 - 0.7 L + 0.1 L2 ) xt = ut 。 特征方程为， (1 - 0.7 L + 0.1 L 2 ) = 0 (1 - 0.2 L) (1- 0.5 L) = 0 特征方程的两个根是，L1 = 5，L2 = 2。因为两个根都在单位圆之外，所以 xt 是平稳的。 解法 3：（观察（φ1, φ2）点是否落在三角区） 从图 1 看，因为（φ1, φ2）= (0.7, -0.1)，落在了 AR(2) 过程的平稳域，落在了过阻尼区， 所以 xt 为平稳过程。 例 3：有 AR(2) 模型 x t = 0.6 x t-1 - 0.1 x t-2 + ut ，试判别 xt 的平稳性。 解： 解法 1：（检查φ1, φ2 约束条件） 1 ˆ φ + = 0.5，- + = -0.7， = - 0.1，满足条件（5）（6）（7），所以 xt 是平稳的。 2 ˆ φ 1 ˆ φ 2 ˆ φ 2 ˆ φ 因为特征方程中各项都是实数，所以其虚根必然是共轭的。 [1- (0.3 - 0.1i ) L ] [1- (0.3 + 0.1i ) L ] = 0 特征方程的两个根是， L1 = 1.03.0 i 1 − = )1.03.0)(1.03.0( )1.03.0( ii i +− + = 3 + i， L2 = 1.03.0 i 1 + = 3 - i， 8

3 +13-1因为两个根都在单位圆之外，所以x是平稳的随机过程。解法3：（观察（，）点是否落在三角区）从图1看，因为（，）=(0.6,-0.1)，落在了AR(2）过程的平稳域，落在了欠阻尼区，所以x为平稳过程。例4：有AR(2）模型x,=0.7x-1+0.6xt-2+u，试判别x,的平稳性。解：解法1：（检查，约束条件）+,=1.3，-+Φ=-0.1，Φ=0.6，条件（5）不满足，所以x是非平稳的。解法2：（因式分解求根）由原式得，（1-0.7L-0.6L）x=ut，特征方程为，(1 -0.7 = - 0.6 -2)=0(1 + 0.5 =) (1- 1.2 =)= 0特征方程的两个根是，21=-2，z2=0.83。因为一个根0.83在单位圆内，所以x是一个非平稳的随机过程。解法3：（观察（，）点是否落在三角区）从图1看，因为（，）=(0.7,0.6)，落在了AR(2）过程的非平稳域，所以x,为非平稳过程。对于一般的自回归过程AR(p)，特征多项式(L)= 1 - L - L2 - .. - ,LP=(1 - G L) (1 - G2L).. (1 -G,L)则x，可表达为kpki+_k2(2.8)x,=@-(L) u=(-+...u1-G,L1-G, L1-G, L其中k，k2,.,k是待定系数。x,具有平稳性的条件是(L）必须收敛，即应有Gl1。由上式可看出一个平稳的AR(p)过程可以转换成一个无限阶的移动平均过程（p个无穷级数之和)。保证ARp）过程平稳的必要但不充分的条件是p个自回归系数之和要小于1，即24i=l保证AR(p）过程平稳的充分但不必要条件是p个自回归系数的绝对值之和要小于19

因为两个根都在单位圆之外，所以 xt 是平稳的随机过程。 解法 3：（观察（φ1, φ2）点是否落在三角区） 从图 1 看，因为（φ1, φ2）= (0.6, -0.1)，落在了 AR(2) 过程的平稳域，落在了欠阻尼区， 所以 xt 为平稳过程。 例 4：有 AR(2) 模型 x t = 0.7 x t-1 + 0.6 x t-2 + ut ，试判别 xt 的平稳性。 解： 解法 1：（检查φ1, φ2 约束条件） 1 ˆ φ + = 1.3，- + = -0.1， = 0.6，条件（5）不满足，所以 xt 是非平稳的。 2 ˆ φ 1 ˆ φ 2 ˆ φ 2 ˆ φ 解法 2：（因式分解求根） 由原式得，(1 - 0.7 L - 0.6 L2 ) xt = ut ，特征方程为， (1 - 0.7 z - 0.6 z 2 ) = 0 (1 + 0.5 z ) (1- 1.2 z ) = 0 特征方程的两个根是，z1 = -2，z2 = 0.83。因为一个根 0.83 在单位圆内，所以 xt 是一个非平 稳的随机过程。 解法 3：（观察（φ1, φ2）点是否落在三角区） 从图 1 看，因为（φ1, φ2）= (0.7, 0.6)，落在了 AR(2) 过程的非平稳域，所以 xt 为非平稳 过程。 对于一般的自回归过程 AR (p)，特征多项式 Φ (L) = 1 - φ1 L - φ2 L2 - . - φp Lp = (1 – G1 L) (1 – G2 L) . (1 – Gp L) 则 xt 可表达为 xt = Φ-1 (L) ut = ( LG k 1 -1 1 + LG k 2 -1 2 +. + ) -1 LG k p p ut (2.8) 其中 k1, k 2, ., k p 是待定系数。xt 具有平稳性的条件是Φ-1 (L) 必须收敛，即应有| Gi | 1。 由上式可看出一个平稳的 AR(p)过程可以转换成一个无限阶的移动平均过程（p 个无穷级数 之和）。 保证 AR(p) 过程平稳的必要但不充分的条件是 p 个自回归系数之和要小于 1，即 ∑ <1 = p i i 1 φ 保证 AR(p) 过程平稳的充分但不必要条件是 p 个自回归系数的绝对值之和要小于 1， 9

即1Z0/01-0103+02-03>03+Φ1+2-303>03-1+$2+303>0如果前三个不等式成立，则可以对后两个不等式中的任何一个进行验证。如果后两个中的任何一个成立，则不必再考虑另外一个（另外一个是多余的）。(2）移动平均过程如果一个剔出均值和确定性成分的线性随机过程可用下式表达,=ur+01u-1 +02 u-2+.. +gu-q=(1 + 0,L +2L+... +0L9)u=(L)u(2.9)其中1,02,..，0。是移动平均参数，ut为白噪声过程，则上式称为9阶移动平均过程，记为MA(）。之所以称“移动平均”，是因为x是由q+1个u和u滞后项的加权和构造而成。“移动”指1的变化，“平均”指加权和。由定义知任何一个9阶移动平均过程都是由9+1个白噪声变量的加权和组成，所以任何一个移动平均过程都是平稳的。与移动平均过程相联系的一个重要概念是可逆性（invertibility）。移动平均过程具有可逆性的条件是特征方程。0(2)=(1 +01=+02 2+.. +02)=0(2.10)的全部根的绝对值必须大于1。由（2.9）有（L)x=u。由于（L）可表示为@(L)=(1- HL)(1- H L) .. (1- H, L)所以有mqm,m2①(L)"= ((2.11)1-H,L1-H,L..1- HqLm为待定参数。可见保证MA(q)过程可以转换成一个无限阶自回归过程，即MA(g)具有可逆性的条件(L)"收敛。对于[L|≤1，必须有|H1，j=1，2，，q成立。而H-是特征方程(L)=(1-HL)（1-HL)...1-HgL)=0的根，所以MA(g)过程具有可逆性的条件是特征方程(L)=0的根必须在单位圆之外。（因为x,=(L)u是平稳的，如果变换成(L)x=u后，变得不平稳，显然失去可逆性。）注意，对于无限阶的移动平均过程(o,ut-)=u(1+L + L 2 +.. )x,=(2.12)i=010

即 ∑ = p i i 1 φ 0 1+ φ 1 - φ 2 + φ 3 > 0 1- φ 1φ 3 + φ 2 - φ 3 2 > 0 3 + φ 1 + φ 2 - 3φ 3 > 0 3 - φ 1 + φ 2 + 3φ 3 > 0 如果前三个不等式成立，则可以对后两个不等式中的任何一个进行验证。如果后两个中 的任何一个成立，则不必再考虑另外一个（另外一个是多余的）。 (2) 移动平均过程 如果一个剔出均值和确定性成分的线性随机过程可用下式表达 xt = ut + θ 1 ut –1 +θ 2 ut -2 + . + θ q ut – q = (1 + θ 1L + θ 2 L2 + . +θ q L q ) ut = Θ(L) ut (2.9) 其中θ 1, θ 2, ., θ q 是移动平均参数，ut为白噪声过程，则上式称为 q 阶移动平均过程，记为 MA(q) 。之所以称“移动平均”，是因为 xt 是由 q +1 个 ut和 ut 滞后项的加权和构造而成。 “移动”指 t 的变化，“平均”指加权和。 由定义知任何一个 q 阶移动平均过程都是由 q + 1 个白噪声变量的加权和组成，所以任 何一个移动平均过程都是平稳的。 与移动平均过程相联系的一个重要概念是可逆性（invertibility）。移动平均过程具有可 逆性的条件是特征方程。 Θ(z) = (1 + θ 1 z + θ 2 z 2 + . + θ q z q )= 0 (2.10) 的全部根的绝对值必须大于 1。 由 (2.9) 有Θ (L) -1 xt = ut。由于Θ (L) 可表示为 Θ (L) = (1 – H1 L) ( 1 – H2 L) . (1 – Hq L) 所以有 Θ (L) -1 =（ LH m 1 1 1− + LH m 2 2 1− +.+ HqL mq 1− ）, (2.11) mi 为待定参数。可见保证 MA(q)过程可以转换成一个无限阶自回归过程，即 MA(q)具有可 逆性的条件Θ(L) -1 收敛。对于 | L | ≤ 1，必须有|Hj| 1，j = 1，2，.，q 成立。 而 Hj -1 是特征方程Θ (L) = (1 – H1 L) ( 1 – H2 L) . (1 – Hq L) = 0 的根，所以 MA(q)过程具有 可逆性的条件是特征方程Θ (L) = 0 的根必须在单位圆之外。（因为 x t =Θ (L) ut 是平稳的，如 果变换成Θ (L) -1 xt = ut 后，变得不平稳，显然失去可逆性。） 注意，对于无限阶的移动平均过程 xt = θ i u t -i) = ut (1+θ1 L + θ2 L 2 ∑ +. ) (2.12) ∞ =0i ( 10