《计量经济学》课程授课教案（讲稿）02 一元线性回归模型

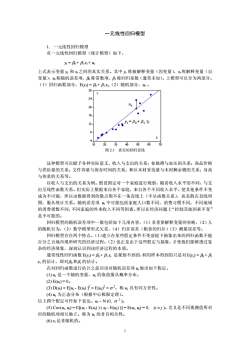
一元线性回归模型1.一元线性回归模型有一元线性回归模型（统计模型）如下，y=+βix+ur上式表示变量y和x之间的真实关系。其中y称被解释变量（因变量），x称解释变量（自变量），u称随机误差项，β称常数项，β称回归系数（通常未知）。上模型可以分为两部分。（1）回归函数部分，E(y)=β+βix，（2）随机部分，ut。284?242016.J=80+81X12X10203040506070图2.1真实的回归直线这种模型可以赋予各种实际意义，收入与支出的关系；如脉搏与血压的关系：商品价格与供给量的关系：文件容量与保存时间的关系；林区木材采伐量与木材剩余物的关系；身高与体重的关系等。以收入与支出的关系为例。假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。但实际上数据来自各个家庭，来自各个不同收入水平，使其他条件不变成为不可能，所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。随机误差项u中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。所以在经济问题上“控制其他因素不变”是不可能的。回归模型的随机误差项中一般包括如下几项内容，（1）非重要解释变量的省略，（2）人的随机行为，（3）数学模型形式欠妥，（4）归并误差（粮食的归并）（5）测量误差等。回归模型存在两个特点。（1)建立在某些假定条件不变前提下抽象出来的回归函数不能百分之百地再现所研究的经济过程。（2）也正是由于这些假定与抽象，才使我们能够透过复杂的经济现象，深刻认识到该经济过程的本质。通常线性回归函数E(y)=β+βix,是观察不到的，利用样本得到的只是对E(y)=β+βx,的估计，即对阝和β的估计。在对回归函数进行估计之前应该对随机误差项u做出如下假定。(1)u是一个随机变量，u的取值服从概率分布。(2) E(u) = 0。(3)D(u)=E[u-E(u)}=E(u)=α。称ui具有同方差性。(4)u为正态分布（根据中心极限定理）。以上四个假定可作如下表达。u~N(0，)。(5)Cov(ui,u)=E[(ui-E(u))（uj-E(u)))=E(ui,u)=0,(ij)。含义是不同观测值所对应的随机项相互独立。称为u的非自相关性。(6)x是非随机的。1

一元线性回归模型 1．一元线性回归模型 有一元线性回归模型（统计模型）如下， yt = β0 + β1 xt + ut 上式表示变量 yt 和 xt 之间的真实关系。其中 yt 称被解释变量（因变量），xt 称解释变量（自 变量），ut 称随机误差项，β0 称常数项，β1 称回归系数（通常未知）。上模型可以分为两部分。 （1）回归函数部分，E(yt) = β0 + β1 xt,（2）随机部分，ut 。 图 2.1 真实的回归直线 这种模型可以赋予各种实际意义，收入与支出的关系；如脉搏与血压的关系；商品价格 与供给量的关系；文件容量与保存时间的关系；林区木材采伐量与木材剩余物的关系；身高 与体重的关系等。 以收入与支出的关系为例。假设固定对一个家庭进行观察，随着收入水平的不同，与支 出呈线性函数关系。但实际上数据来自各个家庭，来自各个不同收入水平，使其他条件不变 成为不可能，所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周 围，服从统计关系。随机误差项 ut 中可能包括家庭人口数不同，消费习惯不同，不同地域 的消费指数不同，不同家庭的外来收入不同等因素。所以在经济问题上“控制其他因素不变” 是不可能的。 回归模型的随机误差项中一般包括如下几项内容，（1）非重要解释变量的省略，（2）人 的随机行为，（3）数学模型形式欠妥，（4）归并误差（粮食的归并）（5）测量误差等。 回归模型存在两个特点。（1）建立在某些假定条件不变前提下抽象出来的回归函数不能 百分之百地再现所研究的经济过程。（2）也正是由于这些假定与抽象，才使我们能够透过复 杂的经济现象，深刻认识到该经济过程的本质。 通常线性回归函数E(yt) = β0 + β1 xt 是观察不到的，利用样本得到的只是对E(yt) = β0 + β1 xt 的估计，即对β0 和β1的估计。 在对回归函数进行估计之前应该对随机误差项 ut 做出如下假定。 (1) ut 是一个随机变量，ut 的取值服从概率分布。 (2) E(ut) = 0。 (3) D(ut) = E[ut - E(ut) ]2 = E(ut) 2 = σ 2 。称 ui 具有同方差性。 (4) ut 为正态分布（根据中心极限定理）。 以上四个假定可作如下表达。ut ∼ N (0, σ 2 )。 (5) Cov(ui, uj) = E[(ui - E(ui) ) ( uj - E(uj) )] = E(ui, uj) = 0, (i ≠ j )。含义是不同观测值所对 应的随机项相互独立。称为 ui 的非自相关性。 (6) xi 是非随机的。 1

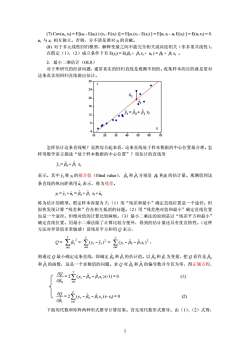
(7)Cov(ui,x)=E[(u;-E(u)) (xi-E(x))]=E[ui (xi-E(x)]=E[uix-u,E(x)]=E(uxi)=0ui与x相互独立。否则，分不清是谁对y的贡献。（8）对于多元线性回归模型，解释变量之间不能完全相关或高度相关（非多重共线性）。在假定（1)，（2）成立条件下有E(y)=E(β+βx,+u,）=β+βx。2.最小二乘估计（OLS）对于所研究的经济问题，通常真实的回归直线是观测不到的。收集样本的且的就是要对这条真实的回归直线做出估计。28.24文20 16.=po+ p xt12oX?10203040506070怎样估计这条直线呢？显然综合起来看，这条直线处于样本数据的中心位置最合理。怎样用数学语言描述“处于样本数据的中心位置”？设估计的直线用j,=βo+ βi x表示。其中j,称y的拟合值（fittedvalue)），β和β,分别是B和β的估计量。观测值到这条直线的纵向距离用，表示，称为残差。y=j,+i,=βo+, x,+it称为估计的模型。假定样本容量为T。（1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。（2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。（3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。（这种方法对异常值非常敏感）设残差平方和用Q表示，7a-含0-)-2-o-m),O=imli=li=l则通过Q最小确定这条直线，即确定β和β,的估计值。以β和β,为变量，把Q看作是β和β的函数，这是一个求极值的问题。求Q对β和β的偏导数并令其为零，得正规方程，只=22(y,-β-βx,)(-1)=0(1)apo=l器-2之(0,-β-x,)(-x)=0(2)下面用代数和矩阵两种形式推导计算结果。首先用代数形式推导。由（1）、（2）式得，2

(7) Cov(ui, xi) = E[(ui - E(ui) ) (xi - E(xi) )] = E[ui (xi - E(xi) ] = E[ui xi - ui E(xi) ] = E(ui xi) = 0. ui 与 xi 相互独立。否则，分不清是谁对 yt 的贡献。 (8) 对于多元线性回归模型，解释变量之间不能完全相关或高度相关（非多重共线性）。 在假定（1），（2）成立条件下有 E(yt) = E(β0 + β1 xt + ut ) = β0 + β1 xt 。 2．最小二乘估计（OLS） 对于所研究的经济问题，通常真实的回归直线是观测不到的。收集样本的目的就是要对 这条真实的回归直线做出估计。 怎样估计这条直线呢？显然综合起来看，这条直线处于样本数据的中心位置最合理。怎 样用数学语言描述“处于样本数据的中心位置”？设估计的直线用 yt = + xt ˆ 0 ˆ β 1 ˆ β 表示。其中 称 yt 的拟合值（fitted value）， 和 分别是 β0 和β1 的估计量。观测值到这 条直线的纵向距离用 表示，称为残差。 t yˆ 0 ˆ β 1 ˆ β ut ˆ yt = + = + xt + t yˆ ut ˆ 0 ˆ β 1 ˆ β ut ˆ 称为估计的模型。假定样本容量为 T。（1）用“残差和最小”确定直线位置是一个途径。但 很快发现计算“残差和”存在相互抵消的问题。（2）用“残差绝对值和最小”确定直线位置 也是一个途径。但绝对值的计算比较麻烦。（3）最小二乘法的原则是以“残差平方和最小” 确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。（这种 方法对异常值非常敏感）设残差平方和用 Q 表示， Q = ∑ = = ， = T i ut 1 2 ˆ ∑= − T i tt yy 1 2 ( ˆ ) ∑= −− T i t t y x 1 2 10 ) ˆˆ ( ββ 则通过 Q 最小确定这条直线，即确定 和 的估计值。以 和 为变量，把 Q 看作是 和 的函数，这是一个求极值的问题。求 Q 对 和 的偏导数并令其为零，得正规方程， 0 ˆ β 1 ˆ β 0 ˆ β 1 ˆ β 0 ˆ β 1 ˆ β 0 ˆ β 1 ˆ β 0 ˆ ∂β ∂Q = 2∑ (-1) = 0 (1) = −− T i t t y x 1 10 ) ˆˆ ( ββ 1 ˆ ∂β ∂Q = 2∑ (- xt) = 0 (2) = −− T i t t y x 1 10 ) ˆˆ ( ββ 下面用代数和矩阵两种形式推导计算结果。首先用代数形式推导。由（1）、（2）式得， 2

(3)Z(y,-β -βix)=0i=lE(yt-Bo -βix,)x=0(4)-（3）式两侧用T除，并整理得，o= J-Bix(5)把上式代入（4）式并整理，得，210 -( -)4-0(6)i=l含0 -)-含(0-),-0(7)isli=lEx,(y, -)β,=(8)E(x, -X)xTTT(x,-X)=0，分别在（8）式的分子和分母上减(y;-)和因为x(y,-)=0,i=lisli=l≥(, -3) 得,islZx(,-)-x(y,-)B=(9)(x, -x)x -Ex(x -x)Z(x, -)(y, -)(10)(x, - x)2下面用矩阵形式推导yBT+B(Zx)=i=li=l.2++(2+)=2）=-Zx,yi=li=li=l[2, [到][][到][区,到[区]-2[[]3

∑ = 0 (3) = −− T i t t y x 1 10 ) ˆˆ ( ββ ∑ xt = 0 (4) = −− T i t t y x 1 10 ) ˆˆ ( ββ （3）式两侧用 T 除，并整理得， 0 ˆ β = xy 1 ˆ − β (5) 把上式代入（4）式并整理，得， ])( ˆ )[( 1 ∑ 1 = −−− T i t t β xxyy xt = 0 (6) ∑ ∑ = = −− − T i tt T i tt xxxxyy 1 1 1 )( ˆ )( β = 0 (7) 1 ˆ β = ∑ ∑ − − tt tt xxx yyx )( )( (8) 因为∑= − T i t yyx 1 )( = 0，∑= − T i t xxx 1 )( = 0，分别在（8）式的分子和分母上减 ∑= − T i t yyx 1 )( 和 ∑= − T i t xxx 1 )( 得， 1 ˆ β = ∑ ∑ ∑ ∑ −−− −−− )()( )()( xxxxxx yyxyyx tt t tt t (9) = ∑ ∑ − −− 2 )( ))(( xx yyxx t t t (10) 下面用矩阵形式推导 T + (∑ ) = 0 ˆ β 1 ˆ β = T i t x 1 ∑= T i t y 1 + ( ) = 0 ˆ β ∑= T i t x 1 1 ˆ β ∑= T i t x 1 2 ∑= T i tt yx 1 = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑∑ ∑ 2 tt t xx xT ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ 1 0 ˆ ˆ β β ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ ∑ tt t yx y = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ 1 0 ˆ ˆ β β 1 2 − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑∑ ∑ tt t xx xT ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ ∑ tt t yx y = 2 2 )( 1 t − ∑∑ t xxT ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − ∑ ∑∑ Tx xx t t t 2 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ ∑ tt t yx y 3

这种形式在单位根检验的理论分析中非常有用。3.最小二乘估计量β和β,的特性(1)线性特性这里指β和β分别是y的线性函数。(x, -)(/-)_(x, -),-(x, -)_(x, -)yB=E(x, -x)2Z(x, -x)Z(x, -x)2(x, -x)令k=(,-，代入上式得,-Zkiy可见β是y的线性函数，是β的线性估计量。同理β也具有线性特性。(2)无偏性利用上式E(β)=E(Zky)=EZk(β+βx,+u)=E(βZk,+βZk,x+Zkut=E[βZk(xrx)+Zkiu]=β+E(Zkiu)=βi(3)有效性B,β的OLS估计量的方差比其他估计量的方差小。Gauss-Marcov定理：若u满足E(u)=0，D(u)=2，那么用OLS法得到的估计量就具有最佳线性无偏性。估计量称最佳线性无偏估计量。最佳线性无偏估计特性保证估计值最大限度的集中在真值周围，估计值的置信区间最小。上面的评价是对有限样本而言，下面讨论估计量的渐近特性。渐近无偏性，一致性和渐近有效性。先给出渐近分布的概念。渐近分布。用T<T<<T表示连续递增样本容量。设在每个样本容量T下重复抽样。则每个xn都应有自己的均值E(xn）与方差Var(xn)。利用递增样本可以求得随机变量序列，XT= [XTI, XT2, --,XTN)其中每个元素都是相应样本容量下的一个随机变量。当T趋于无穷大时，这些分布收敛于某一分布。则称该分布为渐近分布或极限分布。渐近期望。对于期望值序列，E(xT) = (E(x), E(x2), .., E(xTN) )如随着T→80，期望值E(x)收敛于某一常数u，则称μ为x的渐近期望。记为（与期望概念不同）LimE(x)=μ与期望值序列相对应，也可以写出方差序列。Var(x7) =E(x-E(x)=E[xT1 - E(x) , E[xT2 - E(x2) ,..., E[xN - E(XN) )但在许多情形下，LimE(xr-E(xr)=0，即xr的分布退化为一点。例如，已知x的分布是x~4

这种形式在单位根检验的理论分析中非常有用。 3．最小二乘估计量 和 的特性 0 ˆ β 1 ˆ β (1) 线性特性 这里指 和 分别是 β ˆ 0 β ˆ 1 yt的线性函数。 1= ˆ β ∑ ∑ − −− 2 )( ))(( xx yyxx t t t = ∑ ∑ ∑ − −−− 2 )( )()( xx xxyyxx t tt t = ∑ ∑ − − 2 )( )( xx yxx t tt 令 kt = ∑ − − 2 )( )( xx xx t t ，代入上式得 1= ∑ kt yt ˆ β 可见 是β ˆ 1 yt 的线性函数，是β1 的线性估计量。同理β0 也具有线性特性。 (2) 无偏性 利用上式 E( ) = E(∑ kt yt) = E[ ∑ kt (β0 + β1 xt + ut) ] = E ( β0 ∑ kt + β1 ∑ kt xt + ∑ kt ut) 1 ˆ β = E[β1 ∑ kt (xt- x ) + ∑ kt ut ] = β1 + E(∑ kt ut ) = β1 (3) 有效性 β0, β1 的 OLS 估计量的方差比其他估计量的方差小。 Gauss-Marcov 定理： 若 ut 满足 E(ut) = 0，D(ut) = σ 2 ，那么用 OLS 法得到的估计量就具有最佳线性无偏性。 估计量称最佳线性无偏估计量。最佳线性无偏估计特性保证估计值最大限度的集中在真值周 围，估计值的置信区间最小。 上面的评价是对有限样本而言，下面讨论估计量的渐近特性。渐近无偏性，一致性和渐 近有效性。先给出渐近分布的概念。 渐近分布。用 T1 < T2 < .< TN 表示连续递增样本容量。设在每个样本容量 Ti 下重复抽 样。则每个 xTi 都应有自己的均值 E(xTi) 与方差 Var (xTi)。利用递增样本可以求得随机变量 序列， xT = {xT1, xT2, ., xTN} 其中每个元素都是相应样本容量下的一个随机变量。当 TN 趋于无穷大时，这些分布收敛于 某一分布。则称该分布为渐近分布或极限分布。 渐近期望。对于期望值序列， E(xT ) = {E(xT1), E(xT2), ., E(xTN) } 如随着 T → ∞，期望值 E(xT )收敛于某一常数μ，则称μ 为 xT的渐近期望。记为 T )( = μ （与期望概念不同） T xELim∞→ 与期望值序列相对应，也可以写出方差序列。 Var(xT) = E(xT -E(xT))2 ={E[xT1 - E(xT1) ]2 , E[xT2 - E(xT2) ]2 ,., E[xTN - E(xTN ) ]2 } 但在许多情形下， (xT -E(xT))2 E = 0，即 xT的分布退化为一点。例如，已知 T ∞→ Lim x 的分布是 x ∼ 4

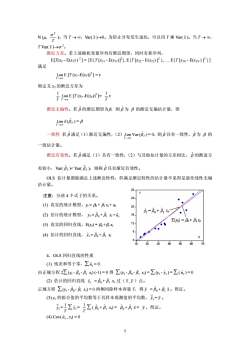
N(H)。当T→80，Var(x）>0。为防止分布发生退化，可以用T乘Var()。当T→0T Var(x)>α?。渐近方差。若上述随机变量序列有渐近期望，同时有新序列，E[T(XT - E())] = {E(T[X1 - E(X)}), E(T[X2 - E(X2)1., E(T[XN- E(XN) )满足Lim E [T (xr-E(x7)"]=v则定义x的渐近方差为Lim E[(a-E(x)IT T→渐近无偏性。若β的渐近期望为β，则β为β的渐近无偏估计量，即Lim E(β)=β致性若β满足（1）渐近无偏性，（2）LimVar(β）=0，则β具有一致性，β为β的一致估计量。渐近有效性。若β满足（1）具有一致性，（2）与其他估计量的方差相比，β的渐进方差较小，Var(βVar(β），则称β具有渐近有效性。OLS估计量都能满足上述渐近特性，但满足渐近特性的估计量不见得是最佳线性无偏估计量。28Y注意：分清4个式子的关系。24(1）真实的统计模型，y=β+βix+ut20J,-po+pi xt16(2）估计的统计模型，y=β+β,x+iE(p)=o+βixt12(3）真实的回归直线，E(y)=B+Bx8.(4）估计的回归直线，,=βo+βxx2050603040704.OLS回归直线的性质(1)残差和等于零，Zi,=0由正规方程2Z(-Bo-x)(-1)=0得Z(y-Bo-x)-Z(-)=Z()=0(2）估计的回归直线，=β+βx过（x）点。正规方程Z(yr-β-βx)=0两侧同除样本容量T，得=β+x。得证。(3)y的拟合值的平均数等于其样本观测值的平均数，=J。-(o+x)=Bo+=。得证。T(4) Cov(u, x) =05

N (μ, T 2 σ )。当 T → ∞，Var( x )→0。为防止分布发生退化，可以用 T 乘 Var( x )。当 T → ∞， T Var( x )→σ 2 。 渐近方差。若上述随机变量序列有渐近期望，同时有新序列， E[T(xT - E(xT) ) 2 ] = {E{T [xT1 - E(xT1)]2 }, E{T [xT2 - E(xT2) ]2 },., E{T [xTN - E(xTN ) ]2 }} 满足 [T (xT -E(xT))2 E ] = v T ∞→ Lim 则定义 xT的渐近方差为 T 1 E T ∞→ Lim [T (xT -E(xT))2 ]= T 1 v 渐近无偏性。若 的渐近期望为 β ˆ β，则 为β ˆ β 的渐近无偏估计量，即 ) = β ˆ ( T T ELim β ∞→ 一致性 若 满足（1）渐近无偏性，（2） = 0，则 具有一致性， 为 β 的 一致估计量。 β ˆ ) ˆ (V T T arLim β ∞→ β ˆ β ˆ 渐近有效性。若 满足（1）具有一致性，（2）与其他估计量的方差相比， 的渐进方 差较小，Var( )< Var( β ˆ β ˆ β T ˆ β T ~ )，则称 具有渐近有效性。 β ˆ OLS 估计量都能满足上述渐近特性，但满足渐近特性的估计量不见得是最佳线性无偏 估计量。 注意：分清 4 个式子的关系。 (1) 真实的统计模型，yt = β0 + β1 xt + ut (2) 估计的统计模型， yt = + xt + 0 ˆ β 1 ˆ β ut ˆ (3) 真实的回归直线，E(yt) = β0 +β1 xt (4) 估计的回归直线， yt = + xt ˆ 0 ˆ β 1 ˆ β 4．OLS 回归直线的性质 (1) 残差和等于零，∑uˆt = 0 由正规方程 2∑(yt - - xt) (-1) = 0 得 ∑(yt - - xt) = ∑(yt - ) = ∑( ) = 0 0 ˆ β 1 ˆ β 0 ˆ β 1 ˆ β t yˆ ut ˆ (2) 估计的回归直线 yˆt = β ˆ 0 + β ˆ 1 xt 过（ x , y ）点。 正规方程 ∑(yt - β ˆ 0 - β ˆ 1 xt) = 0 两侧同除样本容量 T，得 y = 0 + ˆ β 1 ˆ β x 。得证。 (3) yt 的拟合值的平均数等于其样本观测值的平均数， t yˆ = y 。 t yˆ = T 1 ∑ = t yˆ T 1 ∑ ( 0 + xt) = + ˆ β 1 ˆ β 0 ˆ β 1 ˆ β x = y 。得证。 (4) Cov( , xt) = 0 ut ˆ 5

只需证明Z(x-x)u=Zxu-Zxi=Zxu-Zx(-o-x)=0。上式为正规方程之一。(5)Cov(ut,y,)=0只需证明(-)=,-=Z,=i+x)= βZu+pZux=05.y的分布和β,的分布根据假定条件ut~N(0,2)，E(y)=E(Bo+ βix+ u)=Bo+ βix,+ E(u)=Bo+ βixroVar(y) = Var (Bo + βi x, + u) = Var (Bo + βi x.) + Var (u) = ?y,是u,的线性函数，所以Jf~ N(βo+ βix, 2 )。可以证明1E(β)=β,Var(β)=a2Z(x, -x)2β是y的线性函数（β=Zky)，所以1βI~N(βI,0)Z(x, -x)26.的估计定义62= (Zu,)/(T-2)其中2表示待估参数的个数。可以证明E(2）=2。2是的无偏估计量。因为,是残差，所以?又称作误差均方。可用来考察观测值对回归直线的离散程度。β和β.的估计的方差是1Var(B)=S(B)=62Z(x, -x)2Ex?Var(B)=S(Bo)"a,-)627.拟合优度的测量拟合优度是指回归直线对观测值的拟合程度。显然若观测值离回归直线近，则拟合程度好；反之则拟合程度差。6

只需证明 ∑ ( xt - x ) uˆt = ∑ xt uˆt - ∑ x ut ˆ = ∑ xt uˆt = ∑ xt ( - - yˆt β ˆ 0 β ˆ 1 xt) = 0。 上式为正规方程之一。 (5) Cov( , ) = 0 ut ˆ t yˆ 只需证明 ∑ ( -t yˆ y ) uˆt = ∑ yˆt uˆt - ∑ y ut ˆ = ∑ = ∑ ( + xt) t yˆ ut ˆ ut ˆ 0 ˆ β 1 ˆ β = ∑ + ∑ xt = 0 0 ˆ β ut ˆ 1 ˆ β ut ˆ 5．yt 的分布和 的分布 1 ˆ β 根据假定条件 ut ∼ N (0, σ 2 )， E(yt) = E(β0 + β1 xt + ut) = β0 + β1 xt + E(ut) = β0 + β1 xt。 Var(yt) = Var (β0 + β1 xt + ut) = Var (β0 + β1 xt) + Var (ut) = σ 2 yt 是 ut 的线性函数，所以 yt ∼ N (β0 + β1 xt, σ 2 )。 可以证明 E( ) = β1， Var ( ) = 1 ˆ β 1 ˆ β ∑ − 2 )( 1 xxt σ 2 ， 1 ˆ β 是 yt 的线性函数（ = ∑ kt yt），所以 1 ˆ β 1 ˆ β ∼ N (β1, ∑ − 2 )( 1 xxt σ 2 )。 6．σ 2 的估计 定义 2 σˆ = ( ˆ )2() 2 ∑ t Tu − 其中 2 表示待估参数的个数。可以证明 E( ) = σ 2 。 是σ 2 的无偏估计量。因为 是残 差，所以 又称作误差均方。可用来考察观测值对回归直线的离散程度。 2 σˆ 2 σˆ ut ˆ 2 σˆ 1 ˆ β 和 的估计的方差是 0 ˆ β ∧ Var ( ) = S2 ( ) 1 = ˆ β 1 ˆ β ∑ − 2 )( 1 xxt 2 σˆ ， ∧ Var ( ) = S2 ( ) 0 = ˆ β 0 ˆ β ∑ ∑ − 2 2 xxT )( x t t 2 σˆ 7．拟合优度的测量 拟合优度是指回归直线对观测值的拟合程度。显然若观测值离回归直线近，则拟合程度 好；反之则拟合程度差。 6

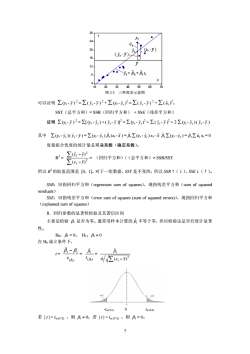
2824.20(Yt-y)(-y)16X12g,=Bo+Bir8X203040506070图2.3三种离差示意图可以证明 (1-)-(-)+-)=(-)2+(u。SST（总平方和）=SSR（回归平方和）+SSE（残差平方和）证明(1-)-[(1-)+(,-)=-+(-+2(1-)(-)其中Z(t-,)(,-)-(-)(xi-x)=(1-)x-xZ(1-)=,Zi,x=0度量拟合优度的统计量是可决系数（确定系数）。Z(,-J)?R?=（回归平方和）/（总平方和）=SSR/SSTZ(y, -j)?所以R的取值范围是[O，1]。对于一组数据，SST是不变的，所以SSRt（+），SSE！（）。SSR：旧指回归平方和（regressionsumofsquares），现指残差平方和（sumof squaredresiduals)SSE：旧指残差平方和（errorsumofsquares（sumofsquarederrors）），现指回归平方和(explainedsumofsquares)8.回归参数的显著性检验及其置信区间主要是检验β是否为零。通常用样本计算的β不等于零，但应检验这是否有统计显著性。Ho: βi= 0;Hi:B*0在Ho成立条件下，Bi-βBS(p)S(p)/ /Z(x, -x)20-1α(T-2)1a(T-2)若/>α(T-2)，则β0;若I<tα(T-2)，则β=0。7

图 2.3 三种离差示意图 可以证明 ∑(yt - y ) 2 = ∑( -t yˆ y ) 2 + ∑(yt - ) 2 = ∑( - t t yˆ yˆ y ) 2 + ∑( u ) ˆt 2 。 SST（总平方和）= SSR（回归平方和） + SSE（残差平方和） 证明 ∑ (yt - y ) 2 = ∑[ (yt - ) + ( - t t yˆ yˆ y )]2 = ∑ (yt - ) 2 + ∑ ( - t t yˆ yˆ y ) 2 + 2 ∑ (yt - )( - t t yˆ yˆ y ) 其中 ∑ (yt - )( - t yˆ t yˆ y ) = ∑ (yt - ) (xt - t yˆ 1 ˆ β x ) = ∑ (yt - ) xt - 1 ˆ β t yˆ x 1 ˆ β ∑ (yt - ) = ∑ xt = 0 t yˆ 1 ˆ β ut ˆ 度量拟合优度的统计量是可决系数（确定系数）。 R2 = ∑ ∑ − − 2 2 )( ( ˆ ) yy yy t t = （回归平方和）/（总平方和）= SSR/SST 所以 R2 的取值范围是 [0，1]。对于一组数据，SST 是不变的，所以 SSR↑（↓），SSE↓（↑）。 SSR：旧指回归平方和（regression sum of squares），现指残差平方和（sum of squared residuals） SSE：旧指残差平方和（error sum of squares (sum of squared errors)），现指回归平方和 （explained sum of squares） 8．回归参数的显著性检验及其置信区间 主要是检验 β1 是否为零。通常用样本计算的 不等于零，但应检验这是否有统计显著 性。 1 ˆ β H0：β1 = 0； H1：β1 ≠ 0 在 H0 成立条件下， t = ) ˆ ( 11 1 ˆ β ββ s − = 1) ˆ ( 1 ˆ β β s = ∑ − 2 1 ˆ )( ˆ xx σ t β -tα (T-2) 0 tα (T-2) 若 | t | > tα (T-2) ，则 β1 ≠ 0；若 | t | < tα (T-2) ，则 β1 = 0。 7

还可以利用β估计β的置信区间。由于p:a-a≤ lα(T-2)) = 1- αS()由大括号内不等式得阝的置信区间BI-S(g) a(T2)≤β≤BI+S(a) ta(T-2)1其中s()是s(）=62的算术根，而其中的是2的算术根。Z(x, -x)29.VF的点预测及其区间预测下面以时间序列数据为例介绍预测问题。预测可分为事前预测和事后预测。两种预测都是在样本区间之外进行，如图所示。对于事后预测，被解释变量和解释变量的值在预测区间都是已知的。可以直接用实际发生值评价模型的预测能力。对于事前预测，解释变量是未发生的。（当模型中含有滞后变量时，解释变量则有可能是已知的。）当预测被解释变量时，则首先应该预测解释变量的值。对于解释变量的预测，通常采用时间序列模型，TiT2T3（目前）样本区间「事后预测|事前预测预测还分为有条件预测和无条件预测。对于无条件预测，预测式中所有解释变量的值都是已知的。所以事后预测应该属于无条件预测。当一个模型的解释变量完全由滞后变量组成时，事前预测也有可能是无条件预测。例如y,=βo+ β xt当预测T+1期的y值时，x用的是T期值，是已知值。预测还分为静态预测和动态预测。(1)yF的点预测。根据估计的回归函数，得ye =βo+β, xp(2)单个yF的区间预测e的分布是(XF -x)21JF~N(B+β xF,(1+)）TE(x, -x)?0,1+1+(xr-3)2所以，yF的区间预测是yp ±[ta(T-2) E(x, -x)2T(3)E(yF）的区间预测E（F）的分布是8

还可以利用 估计 β ˆ 1 β1 的置信区间。由于 P { ) ˆ ( 11 1 ˆ β ββ s − ≤ tα (T-2) } = 1- α 由大括号内不等式得β1 的置信区间 1 ˆ β - tα (T-2) ≤ β1 ≤ + tα (T-2) ) ˆ (β1 s 1 ˆ β ) ˆ (β1 s 其中 是 = ) ˆ (β1 s ) ˆ ( 2 s β1 ∑ − 2 )( 1 xxt 2 σˆ 的算术根，而其中的σˆ 是 的算术根。 2 σˆ 9．yF 的点预测及其区间预测 下面以时间序列数据为例介绍预测问题。预测可分为事前预测和事后预测。两种预测都 是在样本区间之外进行，如图所示。 对于事后预测，被解释变量和解释变量的值在预测区间都是已知的。可以直接用实际发 生值评价模型的预测能力。对于事前预测，解释变量是未发生的。（当模型中含有滞后变量 时，解释变量则有可能是已知的。）当预测被解释变量时，则首先应该预测解释变量的值。 对于解释变量的预测，通常采用时间序列模型。 T1 T2 T3（目前） 样本区间 事后预测 事前预测 预测还分为有条件预测和无条件预测。对于无条件预测，预测式中所有解释变量的值都 是已知的。所以事后预测应该属于无条件预测。当一个模型的解释变量完全由滞后变量组成 时，事前预测也有可能是无条件预测。例如 t yˆ = +0 xt-1 ˆ β 1 ˆ β 当预测 T+1 期的 yt 值时，xt 用的是 T 期值，是已知值。 预测还分为静态预测和动态预测。 (1) yF 的点预测。 根据估计的回归函数，得 = yF + xF ˆ 0 ˆ β 1 ˆ β (2) 单个 yF 的区间预测 F yˆ 的分布是 F yˆ ∼ N (β0 + β1 xF, σ 2 (1+ T 1 + ∑ − − 2 2 )( )( xx xx t F ) ) 所以，yF 的区间预测是 yF ± [ tα (T-2) ˆ σˆ ∑ − − ++ 2 2 )( 1 )( 1 xx xx T t F ] (3) E(yF) 的区间预测 E( yˆ F ) 的分布是 8

E(JF)~N(Bo+Bi X,o(+aF-))Z(x, -x)(xp-x)?1则E(yF）的区间预测是JF ±[ta(T-2) Z(x, - x)2VTt10.案例：用回归模型预测木材剩余物（file:b1c3）伊春林区位于黑龙江省东北部。全区有森林面积218.9732万公项，木材蓄积量为2.324602亿m。森林覆盖率为62.5%，是我国主要的木材工业基地之一。1999年伊春林区木材采伐量为532万m。按此速度44年之后，1999年的蓄积量将被采伐一空。所以目前驱待调整木材采伐规划与方式，保护森林生态环境。为缓解森林资源危机，并解决部分职工就业问题，除了做好木材的深加工外，还要充分利用木材剩余物生产林业产品，如纸浆、纸袋、纸板等。因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。下面，利用一元线性回归模型预测林区每年的木材剩余物。显然引起木材剩余物变化的关键因素是年木材采伐量。给出伊春林区16个林业局1999年木材剩余物和年木材采伐量数据如表2.1。散点图见图2.14。观测点近似服从线性关系。建立一元线性回归模型如下：yi=+Bx+u表2.1年剩余物y和年木材采伐量x数据林业局名年木材剩余物y（万m）年木材采伐量x（万m）乌伊岭26.1361.4东风23.4948.3新青21.9751.8红星11.5335.9五营7.1817.8上甘岭6.8017.0友好18.4355.0翠峦11.6932.7乌马河6.8017.0美溪9.6927.3大丰7.9921.5南岔12.1535.5带岭6.8017.0朗乡17.2050.0桃山9.5030.0双丰5.5213.8合计202.87532.00284242016128X0203040506070图2.14年剩余物y和年木材采伐量x散点图9

E( ) ∼ N (β0 + β1 xF, σ 2 ( F yˆ T 1 + ∑ − − 2 2 )( )( xx xx t F ) ) 则 E(yF) 的区间预测是 yF ± [ tα (T-2) ˆ σˆ ∑ − − + 2 2 )( 1 )( xx xx T t F ] 10．案例：用回归模型预测木材剩余物（file:b1c3） 伊春林区位于黑龙江省东北部。全区有森林面积 218.9732 万公顷，木材蓄积量为 2.324602 亿 m 3 。森林覆盖率为 62.5%，是我国主要的木材工业基地之一。1999 年伊春林区 木材采伐量为 532 万 m 3 。按此速度 44 年之后，1999 年的蓄积量将被采伐一空。所以目前 亟待调整木材采伐规划与方式，保护森林生态环境。为缓解森林资源危机，并解决部分职工 就业问题，除了做好木材的深加工外，还要充分利用木材剩余物生产林业产品，如纸浆、纸 袋、纸板等。因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。下 面，利用一元线性回归模型预测林区每年的木材剩余物。显然引起木材剩余物变化的关键因 素是年木材采伐量。 给出伊春林区 16 个林业局 1999 年木材剩余物和年木材采伐量数据如表 2.1。散点图见 图 2.14。观测点近似服从线性关系。建立一元线性回归模型如下： yt = β0 + β1 xt + ut 表 2.1 年剩余物 yt 和年木材采伐量 xt 数据 林业局名 年木材剩余物 y（万t m3 ）年木材采伐量 x（万t m3 ） 乌伊岭 26.13 61.4 东风 23.49 48.3 新青 21.97 51.8 红星 11.53 35.9 五营 7.18 17.8 上甘岭 6.80 17.0 友好 18.43 55.0 翠峦 11.69 32.7 乌马河 6.80 17.0 美溪 9.69 27.3 大丰 7.99 21.5 南岔 12.15 35.5 带岭 6.80 17.0 朗乡 17.20 50.0 桃山 9.50 30.0 双丰 5.52 13.8 合计 202.87 532.00 图 2.14 年剩余物 yt 和年木材采伐量 xt 散点图 9

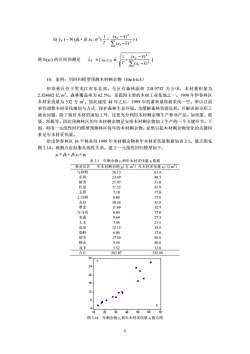
Dependent Variable:YMethod:Least SquaresDate:10/09/033Time:15:38Sample:116Includedobservations:16VariableProb.CoefficientStd. Errort-StatisticC-0.7629281.220966-0.6248560.5421X0.4042800.00000.03337712.11266R-squared0.912890Mean dependent var12.679386.665466Adjusted R-squared0.906668S.D.dependent varS.E.of regression4.3766332.036319Akaike info criterion58.05231Schwarz criterion4.473207Sum squared resid-33.01306Log likelihoodF-statistic146.7166Durbin-Watson stat1.481946Prob(F-statistic)0.000000图2.15EViews输出结果EViews估计结果见图2.15。建立EViews数据文件的方法见附录1。在已建立Eviews数据文件的基础上，进行OLS估计的操作步骤如下：打开工作文件，从主菜单上点击Quick键，选EstimateEquation功能。在出现的对话框中输入ycX。点击Ok键。立即会得到如图2.15所示的结果。下面分析EViews输出结果。先看图2.15的最上部分。被解释变量是yr估计方法是最小二乘法。本次估计用了16对样本观测值。输出格式的中间部分给出5列。第1列给出截距项（C）和解释变量x。第2列给出第1列相应项的回归参数估计值（β和β）。第3列给出相应回归参数估计值的样本标准差（s(βo),s(β,))。第4列给出相应t值。第5列给出t统计量取值大于用样本计算的t值（绝对值）的概率值。以1=12.11266为例，相应概率0.0000表示统计量1取值（绝对值）大于12.1的概率是一个比万分之一还小的数。换句话说，若给定检验水平为0.05，则临界值为t0.05(14)=2.15。1=12.1>2.15落在了Ho的拒绝域，所以结论是β不为零。输出格式的最下部分给出了评价估计的回归函数的若于个统计量的值。依纵向顺序，这些统计量依次是可决系数R、调整的可决系数R2（第3章介绍）、回归函数的标准差（s.e.，即均方误差的算术根）、残差平方和、对数极大似然函数值（第2章介绍）、DW统计量的值、被解释变量的平均数（j）、被解释变量的标准差（s(y,））、赤池（Akaike）信息准则（是一个选择变量最优滞后期的统计量）、施瓦茨（Schwatz）准则（是一个选择变量最优滞后期的统计量）、F统计量（第3章介绍）的值以及F统计量取值大于该值的概率。注意：S.D.和s.e.的区别。s.e.和SSE的关系。根据EViews输出结果（图2.15），写出OLS估计式如下：,=-0.7629 + 0.4043 x(2.64)R=0.91,s.e.=2.04(-0.6)(12.1)其中括号内数字是相应1统计量的值。s.e.是回归函数的标准误差，即=Zi2/16-2)1R是可决系数。R2=0.91说明上式的拟合情况较好。y变差的91%由变量x解释。检验回归系数显著性的原假设和备择假设是（给定α=0.05）Ho:β=0;Hi:β+010

图 2.15 EViews 输出结果 EViews 估计结果见图 2.15。建立 EViews 数据文件的方法见附录 1。在已建立 Eviews 数据文件的基础上，进行 OLS 估计的操作步骤如下：打开工作文件，从主菜单上点击 Quick 键，选 Estimate Equation 功能。在出现的对话框中输入 y c x。点击 Ok 键。立即会得到如图 2.15 所示的结果。 下面分析 EViews 输出结果。先看图 2.15 的最上部分。被解释变量是 yt。估计方法是最 小二乘法。本次估计用了 16 对样本观测值。输出格式的中间部分给出 5 列。第 1 列给出截 距项（C）和解释变量 xt。第 2 列给出第 1 列相应项的回归参数估计值（ 和 ）。第 3 列 给出相应回归参数估计值的样本标准差（s( ), s( )）。第 4 列给出相应 t 值。第 5 列给出 t 统计量取值大于用样本计算的 t 值（绝对值）的概率值。以 t = 12.11266 为例，相应概率 0.0000 表示统计量 t 取值（绝对值）大于 12.1 的概率是一个比万分之一还小的数。换句话说， 若给定检验水平为 0.05，则临界值为 t0.05 (14) = 2.15。t = 12.1>2.15 落在了 H0 的拒绝域，所以 结论是β1 不为零。输出格式的最下部分给出了评价估计的回归函数的若干个统计量的值。依 纵向顺序，这些统计量依次是可决系数 R2 、调整的可决系数 0 ˆ β 1 ˆ β 0 ˆ β 1 ˆ β 2 R （第 3 章介绍）、回归函数 的标准差（s.e.，即均方误差的算术根σˆ ）、残差平方和、对数极大似然函数值（第 2 章介绍）、 DW 统计量的值、被解释变量的平均数（ y ）、被解释变量的标准差（ ）、赤池（Akaike） 信息准则（是一个选择变量最优滞后期的统计量）、施瓦茨（Schwatz）准则（是一个选择变 量最优滞后期的统计量）、F 统计量（第 3 章介绍）的值以及 F 统计量取值大于该值的概率。 )t ( ys 注意：S.D.和 s.e.的区别。s.e.和 SSE 的关系。 根据 EViews 输出结果（图 2.15），写出 OLS 估计式如下： t yˆ = -0.7629 + 0.4043 xt (2.64) (-0.6) (12.1) R2 = 0.91, s. e. = 2.04 其中括号内数字是相应 t 统计量的值。s.e.是回归函数的标准误差，即σˆ = ˆ )216( 2 ut −∑ 。 R2 是可决系数。R 2 = 0.91 说明上式的拟合情况较好。yt 变差的 91%由变量 xt 解释。检验回 归系数显著性的原假设和备择假设是（给定α = 0.05） H0：β1 = 0； H1：β1 ≠ 0 10