《计量经济学》课程教学资源（实验指导）实验九 协整与误差修正模型

实验九协整与误差修正模型【实验目的】掌握单根检验、协整检验以及误差修正模型的估计【实验内容】消费模型的协整检验和误差修正模型的估计【实验步骤】【例1]表9-1中为美国1929年到1994年实际可支配收入x与实际消费水平y统计资料，对消费模型的协整检验和建立误差修正模型表 9-1 可支配收入x与实际消费水平y统计资料实际消费实际可支实际可支实际消费配收入x水平y配收入x水平yyearyear1929585.81962554. 51414. 81293. 31930542.252019631461.11341.9519.7501196419311562.21417. 219651932449. 8456. 61653.514974371933447.419661734.31573. 819344621967461. 11811.41622. 41935505.2487. 619681886.81707. 51936565.9534. 419691947. 41771.21937554.61970585.52025.31813.51938547.6542.219712099.91873. 71939590. 3568. 719722186.21978.4627.2595. 2197319402334. 12066.71941713.9629. 3197423172053.81942824. 71975628.72355.42097.51943863.8647. 319762440.92207.3901.8671.2197719442512.62296.619451978890. 9714. 62638.42391.81946860779. 119792710.12448. 41947793. 31980826. 12733.62447.11948872.981319812795.82476.91949874.5831.419822820.42503.71950942.5874.319832619. 42893.61951978.2894.719843080.12746. 119521009. 7923. 419853162.12865.819531053. 5962.519863261.92969.119541071. 5987.319873289.63052.219551130.8104719883404.33162.419561185. 219891078.73464. 93223.319571214.61104.419903524.53272.6

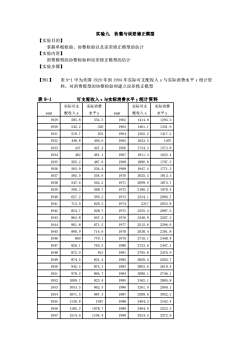
实验九 协整与误差修正模型 【实验目的】 掌握单根检验、协整检验以及误差修正模型的估计 【实验内容】 消费模型的协整检验和误差修正模型的估计 【实验步骤】 【例1】 表 9-1 中为美国 1929 年到 1994 年实际可支配收入 x 与实际消费水平 y 统计资 料，对消费模型的协整检验和建立误差修正模型 表 9-1 可支配收入 x 与实际消费水平 y 统计资料 year 实际可支 配收入 x 实际消费 水平 y year 实际可支 配收入 x 实际消费 水平 y 1929 585.8 554.5 1962 1414.8 1293.3 1930 542.2 520 1963 1461.1 1341.9 1931 519.7 501 1964 1562.2 1417.2 1932 449.8 456.6 1965 1653.5 1497 1933 437 447.4 1966 1734.3 1573.8 1934 462 461.1 1967 1811.4 1622.4 1935 505.2 487.6 1968 1886.8 1707.5 1936 565.9 534.4 1969 1947.4 1771.2 1937 585.5 554.6 1970 2025.3 1813.5 1938 547.6 542.2 1971 2099.9 1873.7 1939 590.3 568.7 1972 2186.2 1978.4 1940 627.2 595.2 1973 2334.1 2066.7 1941 713.9 629.3 1974 2317 2053.8 1942 824.7 628.7 1975 2355.4 2097.5 1943 863.8 647.3 1976 2440.9 2207.3 1944 901.8 671.2 1977 2512.6 2296.6 1945 890.9 714.6 1978 2638.4 2391.8 1946 860 779.1 1979 2710.1 2448.4 1947 826.1 793.3 1980 2733.6 2447.1 1948 872.9 813 1981 2795.8 2476.9 1949 874.5 831.4 1982 2820.4 2503.7 1950 942.5 874.3 1983 2893.6 2619.4 1951 978.2 894.7 1984 3080.1 2746.1 1952 1009.7 923.4 1985 3162.1 2865.8 1953 1053.5 962.5 1986 3261.9 2969.1 1954 1071.5 987.3 1987 3289.6 3052.2 1955 1130.8 1047 1988 3404.3 3162.4 1956 1185.2 1078.7 1989 3464.9 3223.3 1957 1214.6 1104.4 1990 3524.5 3272.6

1958123619913259.41122.23538.519591284.91178.919923349.53648.1196013131210.819933704.13458.7196119941356.41238.43835.43578.5一、单位根检验在检验过程中，若ADF检验值的绝对值大于临界值的绝对值，则认为被检验的序列为平稳序列。检验的顺序为：模型 II:AX,=α+βt+(p-1)X,- + Z P,AX,- +8,i=1,2,.1.用模型III的ADFte分布来检验p=1。如果原假设被拒绝，我们得出结论：X不存在单根。否则，继续第二步。2.使用模型III的ADFtB，给定p=1，检验β=0。如果原假设被拒绝，我们需要利用正态分布来检验0=1：见下面第三步。否则，继续判断和检验模型II，3．使用正态分布检验p=1。如果原假设被拒绝，我们得出结论：不存在单根。否则，我们认为数据序列是不稳定的，并使用差分数据重新开始检验过程。模型 I:AX,=α+(p-1)X,-I+Z P,AX,-,+8,i=1,2,-1.用模型ⅡI的ADFtp分布来检验p=1。如果原假设被拒绝，我们得出结论：X不存在单根。否则，继续第二步。2.使用模型II的ADFta，给定p=1，检验α=0。如果原假设被拒绝，我们需要利用正态分布来检验p=1，见下面第三步。否则，继续判断和检验模型I。3．使用正态分布检验p=1。如果原假设被拒绝，我们得出结论：不存在单根。否则，我们认为数据序列是不稳定的，并使用差分数据重新开始检验过程。模型 I:AX,=α+(p-1)X,-I+Z P,AX,- +8,i=1,2,.使用模型I的ADFte分布来检验p=1。如果原假设被拒绝，我们得出结论：X不存在单根。否则，我们认为数据序列是不稳定的，并使用差分数据重新开始检验过程。利用美国1929年到1994年可支配收入x与消费水平y统计资料进行单位根检验：在此我们先以对Y的检验为例，在主菜单中选择Quick/SeriesStatistics/UnitRootTest屏幕提示用户输入待检验序列名，输入Y，单击OK进入单位根检验定义的对话框，如图9-1

1958 1236 1122.2 1991 3538.5 3259.4 1959 1284.9 1178.9 1992 3648.1 3349.5 1960 1313 1210.8 1993 3704.1 3458.7 1961 1356.4 1238.4 1994 3835.4 3578.5 一、单位根检验 在检验过程中，若 ADF 检验值的绝对值大于临界值的绝对值，则认为被检验的序列为 平稳序列。检验的顺序为： 模型 III: 1 1,2, ( 1) t t i t i t i X t X X      − − =  = + + − +  +  1．用模型 III 的 ADFt分布来检验=。如果原假设被拒绝，我们得出结论：X 不存在 单根。否则，继续第二步。 2．使用模型 III 的 ADFt，给定=，检验β=。如果原假设被拒绝，我们需要利用正 态分布来检验=，见下面第三步。否则，继续判断和检验模型。 ．使用正态分布检验=。如果原假设被拒绝，我们得出结论：不存在单根。否则， 我们认为数据序列是不稳定的，并使用差分数据重新开始检验过程。 模型 II: 1 1,2, ( 1) t t i t i t i X X X     − − =  = + − +  +  1．用模型 II 的 ADFt分布来检验=。如果原假设被拒绝，我们得出结论：X 不存在单 根。否则，继续第二步。 2．使用模型 II 的 ADFtα，给定=，检验α=。如果原假设被拒绝，我们需要利用正 态分布来检验=，见下面第三步。否则，继续判断和检验模型。 ．使用正态分布检验=。如果原假设被拒绝，我们得出结论：不存在单根。否则，我 们认为数据序列是不稳定的，并使用差分数据重新开始检验过程。 模型 I: 1 1,2, ( 1) t t i t i t i X X X     − − =  = + − +  +  使用模型 I 的 ADFt分布来检验=。如果原假设被拒绝，我们得出结论：X 不存在单根。 否则，我们认为数据序列是不稳定的，并使用差分数据重新开始检验过程。 利用美国 1929 年到 1994 年可支配收入 x 与消费水平 y 统计资料进行单位根检验： 在此我们先以对 Y 的检验为例，在主菜单中选择 Quick/Series Statistics/Unit Root Test， 屏幕提示用户输入待检验序列名，输入 Y，单击 OK 进入单位根检验定义的对话框，如图 9-1

Unit Root IestXTesttypeAugmentedDickey-Fuller4Test for unit root inLaglengthLevelCAutomaticselection:Ist differenceSchwarz Info Criterion-2nd differenceMaximumlags:10Include in testequationInterceptCUser specified:CTrend and interceptCNoneOKCancel图9-1单位根检验定义的对话框对话框由三部分构成。检验类型（TestType）中默认项是ADF检验,其他还包括PP检验、DF检验等。TestforunitrootIn中可选择的是对原序列、一阶差分序列或是二阶差序列做单位根检验，在此我们保持默认的level,即原序列。左下方的Includeintestequation中，有三个选项，依次为含常数项，含常数项和趋势项，没有常数项且没有趋势。默认最大滞后期为10，系统默认根据SC最小准则来确定滞后期数。也可以自定滞后期的长度。选择有常数项和趋势项，自定义滞后期的长度为3，见图9-2。区Unit Root IestTesttypeAugmented Dickey-FullerTest forunit rootinLag lengthCLevelCAutomatic selection:CIst differenceSchwarzInfo CriterionC2nd differenceMaximum lags:IncludeintestequationCInterceptuser specified:3Trend and interceptCNoneOKCancel图9-2单位根检验自定义的对话框①有关是否包含常数项和趋势项，比较有效的方法可以用画图法来确定，但是对于一些数据生成过程较为复杂，很难直观地判定。这就需要对常数项、时间趋势与单位根前面系数进行反复的检验。具体检验过程可以参照林光平(2003)

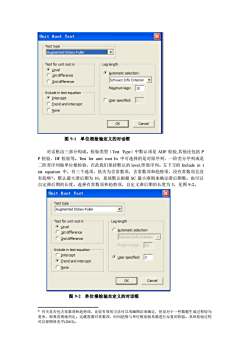
图 9-1 单位根检验定义的对话框 对话框由三部分构成。检验类型（Test Type）中默认项是 ADF 检验,其他还包括 P P 检验、DF 检验等。Test for unit root In 中可选择的是对原序列、一阶差分序列或是 二阶差序列做单位根检验，在此我们保持默认的 level,即原序列。左下方的 Include in t est equation 中，有三个选项，依次为含常数项，含常数项和趋势项，没有常数项且没 有趋势①。默认最大滞后期为 10，系统默认根据 SC 最小准则来确定滞后期数。也可以 自定滞后期的长度。选择有常数项和趋势项，自定义滞后期的长度为 3，见图 9-2。 图 9-2 单位根检验自定义的对话框 ① 有关是否包含常数项和趋势项，比较有效的方法可以用画图法来确定，但是对于一些数据生成过程较为 复杂，很难直观地判定。这就需要对常数项、时间趋势与单位根前面系数进行反复的检验。具体检验过程 可以参照林光平(2003)

在检验的结果输出窗口中(如图9-3)，右上方为ADF检验值，右下方为依次1%、5%和10%的显著水平下的临界值，从图中可以看出ADF统计的检验值为-1.10,其绝对值小于5%的显著水平的临界值-3.48。因此，单位根被清晰地显示出来。给定存在单位根，继续步骤2，检验趋势变量的零值系数假设。基于趋势项的ADF-t统计量的临界值见附表1。不存在趋势的假设在10%的显著性水平下刚刚被拒绝，该10%的临界值为2.38。注意，这里的t统计量不同于我们在做最小二乘时用的t统计值。然后根据步骤3，对传统正态性检验单位根的确认，接受原假设。从上面的分析我们可以认为该序列为非平稳的序列，且该序列有趋势项和常数项。Series: Y forkfile: SHIYANg::Untitledy口回区View ProcObject PropertiesPrint Name FreezeSample Genr Sheet|Graph Stats IdentAugmentedDickey-FullerUnitRootTestonYNull Hypothesis: Y has a unit rootExogenous:Constant, Linear TrendLagLength:3(Fixed)t-StatisticProb.*Augmented Dickey-Fullertest statistic-1.1003220.92051%level-4.113017Test criticalvalues:5%level-3.48397010%level-3.170071*MacKinnon(1996)one-sidedp-valuesAugmented Dickey-Fuller Test EquationDependentVariable:D(Y)Method:LeastSquaresDate:04/25/11Time:09:36Samnle(adiusted)-19331994图9-3单位根检验结果的输出窗口由于水平数据非平稳的，再做一阶差分变换进而再进行估计和单位根检验。在图中的TestforunitrootIn中选差分一阶，同时在Includeintestequation中选取含趋势项和常数项这一项，我们同样根据SC最小来选择滞后两期，发现0阶最好，见图9-4。?在基于5%临界水平下被接受，5%显著性水平的临界值为2.81。有鉴于此，我们使用了基于F-统计量的ADFΦ-检验，临界值见附表2。发现在5%的临界水平下仍然拒绝。因此，综合两种方法考虑，拒绝趋势项系数为0的假设

在检验的结果输出窗口中(如图 9-3)，右上方为 ADF 检验值，右下方为依次 1%、5%和 １0%的显著水平下的临界值，从图中可以看出 ADF 统计的检验值为-1.10,其绝对值小于 5% 的显著水平的临界值–3.48。因此，单位根被清晰地显示出来。给定存在单位根，继续步骤 2， 检验趋势变量的零值系数假设。基于趋势项的 ADF-t 统计量的临界值见附表 1。不存在趋势 的假设在 10%的显著性水平下刚刚被拒绝，该 10%的临界值为 2.38①。注意，这里的 t 统计 量不同于我们在做最小二乘时用的 t 统计值。然后根据步骤 3，对传统正态性检验单位根的 确认，接受原假设。从上面的分析我们可以认为该序列为非平稳的序列，且该序列有趋势项 和常数项。 图 9-3 单位根检验结果的输出窗口 由于水平数据非平稳的，再做一阶差分变换进而再进行估计和单位根检验。在图中的 Test for unit root In 中选差分一阶，同时在 Include in test equation 中选取含趋势项和常数项这 一项，我们同样根据 SC 最小来选择滞后两期，发现 0 阶最好,见图 9-4。 ① 在基于 5%临界水平下被接受，5%显著性水平的临界值为 2.81。有鉴于此，我们使用了基于 F-统计量的 ADFΦ-检验，临界值见附表 2。发现在 5%的临界水平下仍然拒绝。因此，综合两种方法考虑，拒绝趋势 项系数为 0 的假设

Unit Root IestXTesttypeAugmentedDidkeyFulerATest forunit rootinLaglengthLevelSAutomatic selection:Ist differenceSchwarz Info CriterionT2nd differenceMaximumlags:-Include in test equationCInterceptUser spedifed:0Trend and interceptCNoneOKCancel图9-4差分的单位根检验的自定义窗口结果如图9-5：Series:YForkfile: SHIYANg::Untitledl口回区View ProcObject Properties|Print Name|Freeze|Sample|Genr|Sheet|GraphStats IdentAugmentedDickeyFullerUnitRootTestonD(Y)Null Hypothesis:D(Y)has a unit rootExogenous:Constant,LinearTrendLagLength:0(Fixed)Prob.*t-Statistic-5.5496360.0001AugmentedDickey-Fullerteststatistic-4.107947Testcriticalvalues:1%level5% level-3.48159510%level-3.168695*MacKinnon(1996)one-sidedp-values图9-5差分的单位根检验的输出窗口ADF-t值等于-555，很容易得出一阶差分数据不存在单位根的结论。因此，消费数据序列是一阶单整序列。也即一阶差分可以使数据平稳。以下对可支配收入进行单位根检验，仍然选择水平数据，有趋势项和常数项，并经过调试发现1阶滞后最好

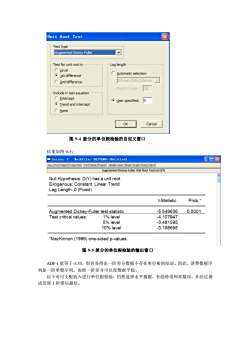
图 9-4 差分的单位根检验的自定义窗口 结果如图 9-5： 图 9-5 差分的单位根检验的输出窗口 ADF-t 值等于-5.55，很容易得出一阶差分数据不存在单位根的结论。因此，消费数据序 列是一阶单整序列。也即一阶差分可以使数据平稳。 以下对可支配收入进行单位根检验，仍然选择水平数据，有趋势项和常数项，并经过调 试发现 1 阶滞后最好

Unit Root Iest+TesttypeAugmentedDickeyFullerTestforunitrootinLaglengthoLevelAutomatic selection:Ist differenceSchwarzInfo Criterion2nd differenceMaximunlags:10Include intestequationCInterceptCUserspecified:Trend and interceptNoneOKCancel图9-6可支配收入单位根检验的自定义窗口结果见图9-7：00×Series:xVorkfile:SHIYANg::UntitlediView Proc Object Properties Print Name Freeze Sample Gerr Sheet Graph Stats IdentAugmented Dickey-FullerUnit RootTest onXNull Hypothesis:X has aunit rootExogenous:Constant,LinearTrendLagLength:1 (Fixed)Prob.*t-StatisticAugmented Dickey-Fullertest statistic-1.7058750.73731%level-4.107947Test critical values:5%level-3.48159510%level-3.168695*MacKinnon(1996)one-sidedp-values图9-7可支配收入单位根检验的自定义窗口根据步骤1.ADF-t统计量和相应的临界值比较，存在单位根。再根据步骤2，在10%显著性水平下，拒绝原假设，我们发现存在趋势项。再根据步骤3，接受原假设，存在单位根。即可支配收入的水平数据是非平稳的。通过一阶差分，选择带常数项和趋势项，滞后一期。结果如图9-8：我们使用了基于F-统计量的ADFΦ-检验，发现在5%的临界水平下仍然拒绝

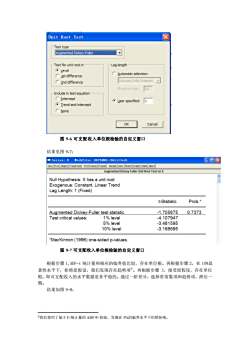
图 9-6 可支配收入单位根检验的自定义窗口 结果见图 9-7： 图 9-7 可支配收入单位根检验的自定义窗口 根据步骤 1,ADF-t 统计量和相应的临界值比较，存在单位根。再根据步骤 2，在 10%显 著性水平下，拒绝原假设，我们发现存在趋势项①。再根据步骤 3，接受原假设，存在单位 根。即可支配收入的水平数据是非平稳的。通过一阶差分，选择带常数项和趋势项，滞后一 期。 结果如图 9-8： ①我们使用了基于 F-统计量的 ADFΦ-检验，发现在 5%的临界水平下仍然拒绝

Series:XWorkfile:SHIYAHg::Untitledy回区View Proc|Object|Properties|Print|Name FreezeSampleGenr Sheet|Graph|Stats|IdentAugmentedDickey-FullerUnit RootTestonD(X)ANull Hypothesis: D(X) has a unit rootExogenous:Constant, Linear TrendLag Length:1 (Fixed)t-StatisticProb.*0.0015Augmented Dickey-Fullerteststatistic-4.749638-4.110440Testcriticalvalues:1%level5%level-3.48276310%level-3.169372*MacKinnon(1996)one-sidedp-values.图9-8可支配收入差分单位根检验的输出窗口ADF-t值等于-4.75，很容易得出可支配收入一阶差分不存在单位根的结论。因此，与消费数据相同，收入数据序列是一阶单整序列。二、协整检验在上面的例子中我们分析出可支配收入为一阶单整序列，同时我们采用同样的分析方法，可知消费支出也为一阶单整。以下检验两者是否具有协整关系。(1)首先对消费方程进行回归，得到回归方程为：Yt=-8.4711+0.9148*Xt(2)再对该回归方程的残差进行单位根检验选择没有常数项，也没有趋势项，滞后期为2。结果如图9-900×Series:EForkfile:SHIYANg::UntitlediView Proc Object Proper tiesPrint Name FreezeSample Genr Sheet Graph Sstats ldentAugmentedDickey-FullerUnitRootTestonENull Hypothesis:E has a unit rootExogenous:NoneLag Length:2 (Fixed)t-StatisticProb.*-3.5146140.0007AugmentedDickey-Fullerteststatistic1%levelTest critical values:-2.6021855%level-1.94607210%level-1.613448*MacKinnon(1996)one-sidedp-values图9-9协整检验ADF-t统计量为-3.52,应该利用后面的附表3，5%置信水平下的临界值为-3.42。因此，变量X和Y之间存在协整关系。可支配收入变化1个单位，消费支出增加0.9148个单位

图 9-8 可支配收入差分单位根检验的输出窗口 ADF-t 值等于-4.75，很容易得出可支配收入一阶差分不存在单位根的结论。因此，与消 费数据相同，收入数据序列是一阶单整序列。 二、协整检验 在上面的例子中我们分析出可支配收入为一阶单整序列，同时我们采用同样的分析方 法，可知消费支出也为一阶单整。以下检验两者是否具有协整关系。 (1)首先对消费方程进行回归，得到回归方程为： Yt = -8.4711 + 0.9148*Xt (2)再对该回归方程的残差进行单位根检验 选择没有常数项，也没有趋势项，滞后期为2。结果如图9-9： 图 9-9 协整检验 ADF-t 统计量为-3.52,应该利用后面的附表 3，5%置信水平下的临界值为-3.42。因此， 变量 X 和 Y 之间存在协整关系。可支配收入变化 1 个单位，消费支出增加 0.9148 个单位

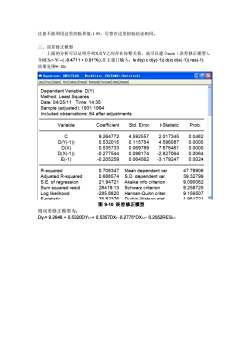
注意不能利用这里的临界值-1.95，尽管在这里检验结论相同。三、误差修正模型上面的分析可以证明序列X及Y之间存在协整关系，故可以建立ecm（误差修正模型）。令RESt=Yt-(-8.4711+0.91Xt),在主窗口输入：Isd(y)cd(y(-1)d(x)d(x(-1))res(-1)结果见图9-10：Equation: UNTITLEDForkfile:SHIYAN9::Untitledy口回区View ProcObjectPrintNameFreezeEstimate Forecaststats ResidsADependentVariable:D(Y)Method:Least SquaresDate:04/25/11Time:14:35Sample(adjusted):19311994Includedobservations:64afteradjustmentsVariableCoefficientStd.Errort-StatisticProb.c9.2647724.5925572.0173450.0482D(Y(-1)0.5320150.1157544.5960870.0000D(X)0.5357330.00000.0697897.676461D(X(-1)-0.2775440.098174-2.8270640.0064E(-1)-0.2052590.064562-3.1792470.0024R-squared0.708347Mean dependent var47.78906Adjusted R-squared0.688574S.D.dependent var39.3279921.947219.090062S.E.of regressionAkaike infocriterionSum squared resid28419.139.258725Schwarzcriterion-285.88209.156507Log likelihoodHannan-Quinncriter35823761Q5171F-etatictinNiirhin_lAatennetat图9-10误差修正模型则误差修正模型为：Dyt=9.2648+0.5320DYt1+0.5357DXt-0.2775*DXt-1-0.2052RESt-1

注意不能利用这里的临界值-1.95，尽管在这里检验结论相同。 三、误差修正模型 上面的分析可以证明序列X及Y之间存在协整关系，故可以建立ecm（误差修正模型）。 令RESt= Yt –( -8.4711 + 0.91*Xt),在主窗口输入：ls d(y) c d(y(-1)) d(x) d(x(-1)) res(-1) 结果见图−： 图 9-10 误差修正模型 则误差修正模型为： Dyt= 9.2648 + 0.5320DYt-1+ 0.5357DXt- 0.2775*DXt-1- 0.2052RESt-1

附表1：基于t统计量的Dickey-Fuller单位根检验临界值Probability to the Right of Critical Value95%90%10%5% 97. 5%2. 5% 99%1%Model Statistic N2. 26-1. 95-1.600.921.331. 70IADFtp252. 662.16502. 622. 25-1. 95-1. 610.911.311. 662. 081002. 60-2. 24-1. 95-1. 610.901. 291. 642. 03-2. 23-1. 610. 891.292502.58-1. 951. 632. 010. 895002.58-2. 23-1. 95-1.611.281. 622.00>500-2. 58-2. 23-1. 95-1. 610. 891.281. 622. 00253. 75-3. 33-3. 00-2. 620. 370.000. 340. 72I1ADF.p50-3.583. 222. 93-2. 60-0. 400. 030. 290. 66100-3. 513. 172. 89-2. 580. 420. 050.260. 63250-3. 46-3. 142. 88-2. 570. 420. 060. 240. 625003. 13-2. 87-2. 570. 430. 070. 243. 440. 61>5003. 12-2. 86-2. 570. 233. 430. 440. 070. 60-4. 38-3. 95-3. 603. 24-1. 140. 800.50IIIADFtp250. 15504. 153. 803. 50-3. 18-1. 190. 870. 580. 241004. 043. 733. 45-3. 151.220. 900. 62-0.28-3. 13250-3. 993. 69-3. 43-1.23-0. 92-0. 64-0. 31-3. 983. 421, 24500-3. 68-3. 130. 930. 650. 32-3.66>5003. 963. 413, 12-1. 25-0. 940. 660. 33Probability toothe Rightof Critical Value1% 2. 5%5%ModelStatisticN10% (Symmetric Distribution, given p = 1)2. 20IIADFta253. 142.972. 61503.282. 892. 182.561003. 222.862.542. 17 2503.192.842. 532. 165003.182.832.522. 16>5003. 182.832.522. 16IIIADFra254.053.593. 202. 77503.873.143.472.781003.783.423.112.733.743. 092503.392.735003.723.383. 082. 72>5003.713.383.082. 72III253. 743.252.852. 39ADFiβ503.603.182.812. 381003.533. 142.792. 382503. 493.122.792. 385003.483.112. 782. 383.46>5003. 112.782.38

附表 1: 基于 t 统计量的 Dickey-Fuller 单位根检验临界值 Probability to the Right of Critical Value Model Statistic N 99% 97.5% 95% 90% 10% 5% 2.5% 1% I ADFt 25 -2.66 -2.26 -1.95 -1.60 0.92 1.33 1.70 2.16 50 -2.62 -2.25 -1.95 -1.61 0.91 1.31 1.66 2.08 100 -2.60 -2.24 -1.95 -1.61 0.90 1.29 1.64 2.03 250 -2.58 -2.23 -1.95 -1.61 0.89 1.29 1.63 2.01 500 -2.58 -2.23 -1.95 -1.61 0.89 1.28 1.62 2.00 >500 -2.58 -2.23 -1.95 -1.61 0.89 1.28 1.62 2.00 II ADFt 25 -3.75 -3.33 -3.00 -2.62 -0.37 0.00 0.34 0.72 50 -3.58 -3.22 -2.93 -2.60 -0.40 -0.03 0.29 0.66 100 -3.51 -3.17 -2.89 -2.58 -0.42 -0.05 0.26 0.63 250 -3.46 -3.14 -2.88 -2.57 -0.42 -0.06 0.24 0.62 500 -3.44 -3.13 -2.87 -2.57 -0.43 -0.07 0.24 0.61 >500 -3.43 -3.12 -2.86 -2.57 -0.44 -0.07 0.23 0.60 III ADFt 25 -4.38 -3.95 -3.60 -3.24 -1.14 -0.80 -0.50 -0.15 50 -4.15 -3.80 -3.50 -3.18 -1.19 -0.87 -0.58 -0.24 100 -4.04 -3.73 -3.45 -3.15 -1.22 -0.90 -0.62 -0.28 250 -3.99 -3.69 -3.43 -3.13 -1.23 -0.92 -0.64 -0.31 500 -3.98 -3.68 -3.42 -3.13 -1.24 -0.93 -0.65 -0.32 >500 -3.96 -3.66 -3.41 -3.12 -1.25 -0.94 -0.66 -0.33 Probability to the Right of Critical Value Model Statistic N 1% 2.5% 5% 10% (Symmetric Distribution, given  = 1) II ADFt 25 3.14 2.97 2.61 2.20 50 3.28 2.89 2.56 2.18 100 3.22 2.86 2.54 2.17 250 3.19 2.84 2.53 2.16 500 3.18 2.83 2.52 2.16 >500 3.18 2.83 2.52 2.16 III ADFt 25 4.05 3.59 3.20 2.77 50 3.87 3.47 3.14 2.78 100 3.78 3.42 3.11 2.73 250 3.74 3.39 3.09 2.73 500 3.72 3.38 3.08 2.72 >500 3.71 3.38 3.08 2.72 III ADFt 25 3.74 3.25 2.85 2.39 50 3.60 3.18 2.81 2.38 100 3.53 3.14 2.79 2.38 250 3.49 3.12 2.79 2.38 500 3.48 3.11 2.78 2.38 >500 3.46 3.11 2.78 2.38

附表2：基于F统计量的Dickey-Fuller单位根检验临界值Probability to the Right of Critical Value5%10% 90%1% 2. 5%95%97. 5%Model StatisticN99%4. 12257. 886.305.180. 650. 49 0.380. 29I1ADFra.p507.065. 804. 863. 940. 660. 500. 300. 291006.705. 574. 713. 860. 670. 500. 300. 292506. 525.454. 633. 810. 670. 510. 390. 305006. 475. 414.613. 790. 670. 510. 390. 303.780. 670. 51>5006. 435. 384. 590. 400. 306.755. 684. 671. 10IIIADFra.pp 258.210. 890. 750. 61507.025.134. 311.120.910.775.940.621006.505.594.884.161. 120. 920. 770. 634. 072506. 225. 404. 751. 130. 920. 770. 635006. 155. 354.714. 051. 130. 920.770. 63>5000. 926. 095.314. 684.031. 130. 770. 637. 245.911. 33I1I2510. 618.651.080.900. 74ADFep509.317.816.735. 611. 371. 110. 930. 761008.737.446. 495.471. 381. 12 0.940.765. 391. 391. 132508.437.256. 340. 940. 765008.347.206.305. 361. 391. 130. 940. 76>5008. 277.166. 255.341.391. 130.940. 77附表 3用于残差回归的 Dickey-Fuller 协整 t统计量临界值K1%5%Mode12. 5%10%223. 96-3. 643. 373. 0734. 314, 023. 773. 4544. 734. 374. 113. 8355. 074. 71-4. 45-4. 1665. 284. 98-4. 71-4. 4322a3. 98-3. 683.42-3. 1334. 364. 073. 80-3. 5244. 654. 394. 16-3. 8455. 044. 774. 49-4. 2065. 365. 024. 744. 4675. 585. 315. 03-4. 73324. 074. 363.803.5234. 654. 39-4. 163. 8445. 044. 77-4. 49-4. 2055. 365. 024. 74-4. 4665. 585.315. 034. 73

附表 2: 基于 F 统计量的 Dickey-Fuller 单位根检验临界值 Probability to the Right of Critical Value Model Statistic N 1% 2.5% 5% 10% 90% 95% 97.5% 99% II ADFF 25 7.88 6.30 5.18 4.12 0.65 0.49 0.38 0.29 50 7.06 5.80 4.86 3.94 0.66 0.50 0.30 0.29 100 6.70 5.57 4.71 3.86 0.67 0.50 0.30 0.29 250 6.52 5.45 4.63 3.81 0.67 0.51 0.39 0.30 500 6.47 5.41 4.61 3.79 0.67 0.51 0.39 0.30 >500 6.43 5.38 4.59 3.78 0.67 0.51 0.40 0.30 III ADFF 25 8.21 6.75 5.68 4.67 1.10 0.89 0.75 0.61 50 7.02 5.94 5.13 4.31 1.12 0.91 0.77 0.62 100 6.50 5.59 4.88 4.16 1.12 0.92 0.77 0.63 250 6.22 5.40 4.75 4.07 1.13 0.92 0.77 0.63 500 6.15 5.35 4.71 4.05 1.13 0.92 0.77 0.63 >500 6.09 5.31 4.68 4.03 1.13 0.92 0.77 0.63 III ADFF 25 10.61 8.65 7.24 5.91 1.33 1.08 0.90 0.74 50 9.31 7.81 6.73 5.61 1.37 1.11 0.93 0.76 100 8.73 7.44 6.49 5.47 1.38 1.12 0.94 0.76 250 8.43 7.25 6.34 5.39 1.39 1.13 0.94 0.76 500 8.34 7.20 6.30 5.36 1.39 1.13 0.94 0.76 >500 8.27 7.16 6.25 5.34 1.39 1.13 0.94 0.77 附表 3 用于残差回归的 Dickey-Fuller 协整 t 统计量临界值 Model K 1% 2.5% 5% 10% 2 2 -3.96 -3.64 -3.37 -3.07 3 -4.31 -4.02 -3.77 -3.45 4 -4.73 -4.37 -4.11 -3.83 5 -5.07 -4.71 -4.45 -4.16 6 -5.28 -4.98 -4.71 -4.43 2a 2 -3.98 -3.68 -3.42 -3.13 3 -4.36 -4.07 -3.80 -3.52 4 -4.65 -4.39 -4.16 -3.84 5 -5.04 -4.77 -4.49 -4.20 6 -5.36 -5.02 -4.74 -4.46 7 -5.58 -5.31 -5.03 -4.73 3 2 -4.36 -4.07 -3.80 -3.52 3 -4.65 -4.39 -4.16 -3.84 4 -5.04 -4.77 -4.49 -4.20 5 -5.36 -5.02 -4.74 -4.46 6 -5.58 -5.31 -5.03 -4.73