《计量经济学》课程教学资源（实验指导）实验四 异方差性

实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国消费函数模型【实验步骤】【例1】表4-1列出了2007年我国31个省市人均GDP(X)与人均消费(Y)的统计资料，请利用统计软件Eviews建立我国消费函数模型。表 4-12007年我国31个省市人均GDP（X）与人均消费（Y）Yx地区XY地区北京湖北6513189115820416206天津1195746122湖南624014492河北广东5674198771266333151山西552516945广西498712555内蒙7062海南55522539314555辽宁796525792重庆654514660吉林四川667519382525912893黑龙江598618478贵州40576915上海2426066367云南455310540江苏9659西藏32153392812109浙江陕西5272125693741114607安徽5278甘肃42741034612045福建877225908青海497814257宁夏江西470212633581614649山东807548901699927807新疆河南514116012一、检验异方差性1.图形分析检验(1)观察销售利润（Y）与销售收入（X）的相关图（图4-1)：SCATXY1

1 实验四 异方差性 【实验目的】 掌握异方差性的检验及处理方法 【实验内容】 建立并检验我国消费函数模型 【实验步骤】 【例1】 表 4-1 列出了 2007 年我国 31 个省市人均 GDP(X)与人均消费(Y)的统计资料，请 利用统计软件 Eviews 建立我国消费函数模型。 表 4-1 2007 年我国 31 个省市人均 GDP(X)与人均消费(Y) 地区 X Y 地区 X Y 北京 18911 58204 湖北 6513 16206 天津 11957 46122 湖南 6240 14492 河北 5674 19877 广东 12663 33151 山西 5525 16945 广西 4987 12555 内蒙 7062 25393 海南 5552 14555 辽宁 7965 25792 重庆 6545 14660 吉林 6675 19382 四川 5259 12893 黑龙江 5986 18478 贵州 4057 6915 上海 24260 66367 云南 4553 10540 江苏 9659 33928 西藏 3215 12109 浙江 12569 37411 陕西 5272 14607 安徽 5278 12045 甘肃 4274 10346 福建 8772 25908 青海 4978 14257 江西 4702 12633 宁夏 5816 14649 山东 8075 27807 新疆 4890 16999 河南 5141 16012 一、检验异方差性 ⒈图形分析检验 ⑴观察销售利润（Y）与销售收入（X）的相关图(图 4-1)：SCAT X Y

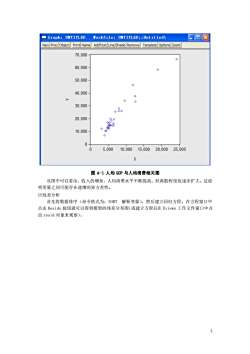
Graph:UHIIILED口回区Workfile:UNIIILED::UntitledvView ProcObject Print NameAddTextLine/ShadeRemoveTemplateOptionsZoom70.000o60.00050.00040.000-30.000-00020.000800a10.000o0-5,00010.000015.00020.00025.000X图4-1人均GDP与人均消费相关图从图中可以看出，收入的增加，人均消费水平不断提高，但离散程度也逐步扩大。这说明变量之间可能存在递增的异方差性。(2)残差分析首先将数据排序（命令格式为：SORT解释变量），然后建立回归方程。在方程窗口中点击Resids按钮就可以得到模型的残差分布图（或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。2

2 图 4-1 人均 GDP 与人均消费相关图 从图中可以看出，收入的增加，人均消费水平不断提高，但离散程度也逐步扩大。这说 明变量之间可能存在递增的异方差性。 ⑵残差分析 首先将数据排序（命令格式为：SORT 解释变量），然后建立回归方程。在方程窗口中 点击 Resids 按钮就可以得到模型的残差分布图（或建立方程后在 Eviews 工作文件窗口中点 击 resid 对象来观察）

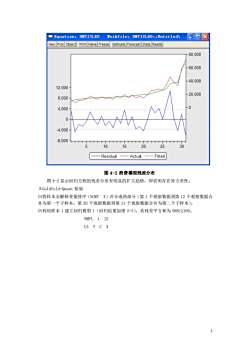
Equation:UHIIILEDForkfile:UHIIILED::UntitledyView ProcObjectPrint Name FreezeEstimateForecast Stats Resids80,00060.00040.00012,000-20,0008.000-4.000-0-4,000-8.00030510152025FittedResidualActual图4-2消费模型残差分布图4-2显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。2.Goldfeld-Quant检验(1)将样本安解释变量排序（SORTX）并分成两部分（第1个观察数据到第12个观察数据合并为第一个子样本，第20个观察数据到第31个观察数据合并为第二个子样本）。(2)利用样本1建立回归模型1（回归结果如图4-3），其残差平方和为58812169。SMPL112LSYCX

3 图 4-2 消费模型残差分布 图 4-2 显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。 ⒉Goldfeld-Quant 检验 ⑴将样本安解释变量排序（SORT X）并分成两部分（第 1 个观察数据到第 12 个观察数据合 并为第一个子样本，第 20 个观察数据到第 31 个观察数据合并为第二个子样本）。 ⑵利用样本 1 建立回归模型 1（回归结果如图 4-3），其残差平方和为 58812169。 SMPL 1 12 LS Y C X

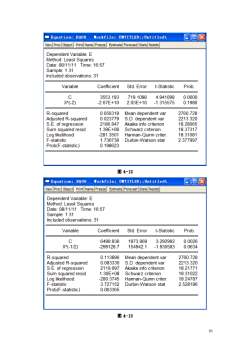
O回×Equation:EQo1Torkfile:UNIIILED::UntitledEstimate Forecast stats ResidsViewProcObjectPrintNameFreezeDependentVariable:YMethod:LeastSquaresDate:08/11/11Time:09:21Sample:112Includedobservations:12VariableStd.Errort-StatisticProb.CoefficientC0.72492040.2825637.5010.361913x2.2511331.1858531.8983240.0869R-squared0.264902Meandependent var12659.250.1913932696.899Adjusted R-squaredS.D. dependent varS.E.of regression2425.12218.57616AkaikeinfocriterionSum squared resid58812169Schwarzcriterion18.65698-109.457018.54624Log likelihoodHannan-QuinncriterF-statistic3.603635Durbin-Watson stat2.0396040.086862Prob(F-statistic)图4-3样本1回归结果(3)利用样本2建立回归模型2（回归结果如图4-4），其残差平方和为225000000。SMPL2031SYCXLS4

4 图 4-3 样本 1 回归结果 ⑶利用样本 2 建立回归模型 2（回归结果如图 4-4），其残差平方和为 225000000。 SMPL 20 31 LS Y C X

口回风Equation: EQ02forkfile:UHIIILED::UntitledyView Proc Object Print Name Freeze Estimate Forecast stats ResidsDependent Variable:YMethod:LeastSquaresDate:08/11/11Time:09:22Sample:2031Includedobservations:12VariableCoefficientStd.Errort-StatisticProb.C3804.8693277.6910.27271.160838x2.7270990.26443710.312860.0000R-squared0.91405634510.42MeandependentvarAdjustedR-squared0.90546215440.92S.D.dependentvarS.E.of regression4747.62719.91969Akaike infocriterion2.25E+0820.00051Sum squaredresidSchwarzcriterion-117.518119.88977Log likelihoodHannan-Quinncriter106.3552F-statisticDurbin-Watson stat1.621173Prob(F-statistic)0.000001图4-4样本2回归结果(4)计算F统计量：F=RSS,/RSS,=225000000/58812169=3.8257，RSS和RSS分别是模型1和模型2的残差平方和。取α=0.05时，查F分布表得Fo.0s(12-1-1,12-1-1)=2.98，而F=3.8257>Fo.05=2.98，所以模型存在异方差性。3.White检验(1)建立回归模型（先利用SMPL命令调整为全样本)：LSYCX，回归结果如图4-5。5

5 图 4-4 样本 2 回归结果 ⑷计算 F 统计量： 2 1 F = RSS / RSS ＝225000000/58812169=3.8257， RSS1和RSS2 分别是 模型 1 和模型 2 的残差平方和。 取  = 0.05 时，查 F 分 布 表 得 0.05 F (12 1 1,12 1 1) 2.98 − − − − = ， 而 0.05 F F =  = 3.8257 2.98 ，所以模型存在异方差性。 ⒊White 检验 ⑴建立回归模型(先利用 SMPL 命令调整为全样本)：LS Y C X，回归结果如图 4-5

Equation: UNIIILEDforkfile:UNIIILED::UntitledyView ProcObjectPrint Name Freeze Estimate Forecast Stats ResidsDependentVariable:YMethod:Least SquaresDate:08/11/11Time:09:46Sample:131Includedobservations:31VariableCoefficientStd.Errort-StatisticProb.c-609.50661286.432-0.4737960.6392x3.0045390.14745820.375590.0000R-squared0.93470921975.42Mean dependent varAdjustedR-squared0.932458S.D.dependentvar13987.64S.E.of regression3635.238Akaike info criterion19.297083.83E+0819.38959SumsquaredresidSchwarzcriterionLog likelihood-297.104719.32724Hannan-Quinncriter415.1649F-statisticDurbin-Watsonstat1.569375Prob(F-statistic)0.000000图4-5全样本回归模型(2)在方程窗口上点击View/ResidualTests)HeteroskedastcityTests，在弹出的对话框中选择White，并点击OK，检验结果如图4-6。Equation:EQ03Torkfile:UHIIILED::Untitled口回×ViewProc ObjectPrintName FreezeEstimateForecast stats Resids一HeteroskedasticityTest:White0.0795F-statistic2.775656EProb.F(2.28)5.129178Prob.Chi-Square(2)0.0770Obs*R-squared0.0374ScaledexplainedSs6.572087Prob.Chi-Square(2)图4-6White检验结果White检验可以利用三种统计量，这三种统计量是渐近一致，但在有限样本情况下，结论可能不一致。取显著水平α=0.05，如利用F值检验，则不存在异方差；如利用nR2检验，由于x0.0s(2)=5.99>nR2=5.1291,所以不存在异方差性。但是利用第三种统计量，则存在异方差。实际应用中可以直接观察相伴概率p值的大小，若p值较小，则认为存在异方差性。反之，则认为不存在异方差性。4.Park检验(1)建立回归模型（结果同图4-5所示）。(2)生成新变量序列：GENRLNE2=1og(RESID~2)GENR LNX=log(x)

6 图 4-5 全样本回归模型 ⑵在方程窗口上点击 View\Residual Tests\ Heteroskedastcity Tests ,在弹出的对话框 中选择 White,并点击 OK,检验结果如图 4-6。 图 4-6 White 检验结果 White 检验可以利用三种统计量，这三种统计量是渐近一致，但在有限样本情况下， 结论可能不一致。取显著水平  = 0.05 ，如利用 F 值检验，则不存在异方差；如利用 2 nR 检验，由于 2 2 0.05  (2) 5.99 5.1291 =  = nR ,所以不存在异方差性。但是利用第三种统计量， 则存在异方差。实际应用中可以直接观察相伴概率 p 值的大小，若 p 值较小，则认为存在异 方差性。反之，则认为不存在异方差性。 ⒋Park 检验 ⑴建立回归模型（结果同图 4-5 所示）。 ⑵生成新变量序列：GENR LNE2=log(RESID^2) GENR LNX=log(X)

(3)建立新残差序列对解释变量的回归模型：LSLNE2CLNX，回归结果如图4-7所示，Equation: UHIIILEDYorkfile: UHIIILED::Untitled口回区View Proc objectPrint Name FreezeEstimateForecast Stats ResidsDependentVariable:LNE2MethodLeastSquaresDate:08/11/11Time:16:44Sample:131Includedobservations:31VariableStd.Errort-StatisticProb.Coefficientc0.33308.6529498.7892880.984488LNX0.7127700.48020.9965160.715262R-squared0.01733614.93168Meandependentvar-0.0165492.434562Adjusted R-squaredS.D.dependentvarS.E.ofregression2.454625Akaikeinfocriterion4.696166174.73034.788681Sum squaredresidSchwarzcriterionLog likelihood-70.790574.726324Hannan-Quinncriter0.5116002.721885F-statisticDurbin-Watson statProb(F-statistic)0.480166图4-7Park检验回归模型从图4-7所示的回归结果中可以看出，不能拒绝LNX的系数估计值为0的假设，即误差项的方差与解释变量不存在较强的相关关系，即认为不存在异方差性。5.Gleiser检验（Gleiser检验与Park检验原理相同）(1)建立回归模型（结果同图4-5所示）。(2)生成新变量序列：GENRE=ABS(RESID)(3)分别建立新残差序列（E）对各解释变量（X/X~2/X~（1/2)/X（一1)/X~（2)/X（—1/2））的回归模型，回归结果如图4-8、4-9、4-10、4-11、4-12、4-13所示。7

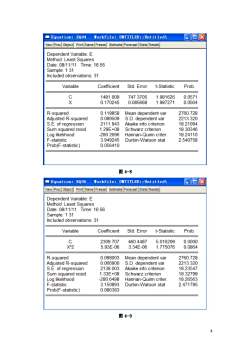
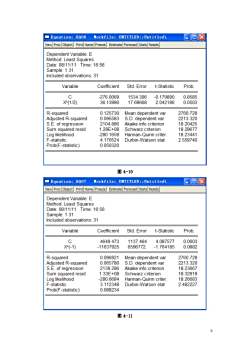
7 ⑶建立新残差序列对解释变量的回归模型：LS LNE2 C LNX，回归结果如图 4-7 所示。 图 4-7 Park 检验回归模型 从图 4-7 所示的回归结果中可以看出，不能拒绝 LNX 的系数估计值为 0 的假设，即误差 项的方差与解释变量不存在较强的相关关系，即认为不存在异方差性。 ⒌Gleiser 检验（Gleiser 检验与 Park 检验原理相同） ⑴建立回归模型（结果同图 4-5 所示）。 ⑵生成新变量序列：GENR E=ABS(RESID) ⑶分别建立新残差序列（E）对各解释变量（X/X^2/X^(1/2)/X^(－1)/ X^(－2)/ X^(－1/2)） 的回归模型，回归结果如图 4-8、4-9、4-10、4-11、4-12、4-13 所示

O回×Equation:EQ04Torkfile:UNIIILED::UntitlediEstimateForecastStatsResidsViewProcObjectPrintNameFreezeDependent Variable:EMethodLeastSquaresDate:08/11/11Time:16.55Sample:131Includedobservations:31Prob.VariableCoefficientStd.Errort-StatisticC0.05711481.009747.37051.981626x0.05640.1702450.0856681.987271R-squared0.119858Meandependent var2760.7280.0895092213.320AdjustedR-squaredS.D. dependent varS.E.ofregression2111.94318.21094AkaikeinfocriterionSumsquaredresid1.29E+08Schwarzcriterion18.30346-280.269618.24110Log likelihoodHannan-Quinn criterF-statistic3.9492452.540758Durbin-Watson stat0.056410Prob(F-statistic)图 4-8口回区Equation: EQ05Yorkfile:UNIIILED::UntitledyView Proc Object Print Name FreezeEstimateForecast StatsResidsDependent Variable:EMethod:LeastSquaresDate:08/11/11Time:16:56Sample:131Includedobservations:31VariableStd.ErrorProb.Coefficientt-StatisticC2309.707460.44870.00005.016209X25.93E-063.34E-061.7750760.0864R-squared0.098003Meandependent var2760.7280.0669002213.320Adjusted R-squaredS.D.dependent varS.E.ofregression2138.00318.23547AkaikeinfocriterionSumsquaredresid1.33E+08Schwarzcriterion18.32799-280.649818.26563Log likelihoodHannan-Quinn criterF-statistic3.1508932.471795Durbin-Watson stat0.086383Prob(F-statistic)图 4-98

8 图 4-8 图 4-9

口回风Equation:EQ06Yorkfile:UNIIILED::UntitlediView Proc Object PrintName FreezeEstimateForecast Stats ResidsDependentVariable:EMethodLeastSquaresDate:08/11/11 Time:16:56Sample:131Includedobservations:31VariableCoefficientStd.Errort-StatisticProb.c0.8585-276.00691534.306-0.179890X(1/2)36.1399017.696682.0421860.0503R-squared0.125730Mean dependent var2760.7280.0955832213.320Adjusted R-squaredS.D.dependent varS.E.of regression2104.88618.20425Akaikeinfo criterion18.29677Sum squared resid1.28E+08Schwarzcriterion-280.165918.23441Log likelihoodHannan-Quinn criter4.170524F-statisticDurbin-Watson stat2.5597400.050320Prob(F-statistic)图4-10口回区Equation: EQoTorkfile:UNTIILED::UntitledtView Proc objectPrint Name Freeze Estimate Forecast Stats ResidsDependentVariable:EMethodLeastSquaresDate:08/11/11Time:16:56Sample:131Includedobservations:31VariableCoefficientStd.Errort-StatisticProb.c4649.4731137.4644.0875770.0003X(-1)-1163792565967720.0882-1.7641852760.728R-squared0.096921Mean dependent varAdjusted R-squared0.065780S.D.dependentvar2213.320S.E.ofregression2139.28618.23667Akaikeinfocriterion1.33E+0818.32919Sum squared residSchwarzcriterion-280.668418.26683Log likelihoodHannan-Quinn criter3.1123482.482227F-statisticDurbin-Watson statProb(F-statistic)0.088234图4-119

9 图 4-10 图 4-11

口回区Equation:EQ08Forkfile:UHIIILED::UntitledyViewProcobjectPrintName FreezeEstimateForecastStatsResidsDependentVariable:EMethod:LeastSquaresDate:08/11/11 Time:16:57Sample:131Includedobservations:31Prob.VariableCoefficientStd.Errort-StatisticC3553.193719.10984.9410990.0000X(-2)-2.67E+100.19862.03E+10-1.315575R-squared2760.7280.056319Meandependent varAdjusted R-squared0.023779S.D.dependent var2213.320S.E.of regression2186.84718.28065Akaike info criterion18.37317Sum squared resid1.39E+08SchwarzcriterionLog likelihood-281.3501Hannan-Quinn criter18.310811.7307382.377997F-statisticDurbin-Watson statProb(F-statistic)0.198623图4-12口回×Equation:EQogorkfile:UNIIILED::UntitlediView Proc Object Print Name FreezeEstimateForecast Stats ResidsDependent Variable:EMethod:LeastSquaresDate:08/11/11Time:16:57Sample:131Includedobservations:31VariableProb.CoefficientStd.Errort-StatisticC0.00266499.9361973.8693.292992X(-1/2)-299128.7154942.1-1.9305830.0634R-squared0.1138862760.728MeandependentvarAdjusted R-squared0.083330S.D.dependent var2213.320S.E.ofregression2119.097Akaikeinfocriterion18.21771Sum squared resid1.30E+08Schwarz criterion18.31022-280.374518.24787Log likelihoodHannan-Quinn criter.F-statistic3.7271522.528186Durbin-Watsonstat0.063365Prob(F-statistic)图4-1310

10 图 4-12 图 4-13