《计量经济学》课程授课教案（讲稿）04 非线模型的线化

非线性回归模型的线性化以上介绍了线性回归模型。但有时候变量之间的关系是非线性的。例如y=αo+aix,β+uy,=αoer+u上述非线性回归模型是无法用最小二乘法估计参数的。可采用非线性方法进行估计。估计过程非常复杂和困难，在20世纪40年代之前几乎不可能实现。计算机的出现大大方便了非线性回归模型的估计。专用软件使这种计算变得非常容易。但本章不是介绍这类模型的估计。另外还有一类非线性回归模型。其形式是非线性的，但可以通过适当的变换，转化为线性模型，然后利用线性回归模型的估计与检验方法进行处理。称此类模型为可线性化的非线性模型。下面介绍几种典型的可以做线性化处理的非线性模型。(1）指数函数模型y,= aeb,+n,(4.1)b>0和b0)图4.2y,=aebx,+i,(b0和b<0两种情形的图形分别见图4.3和4.4。x,和y的关系是非线性的。令x*=Lnxt则(4.5)y,=a+bx*+ut变量y和x*已变换成为线性关系。1

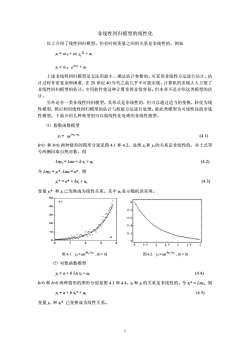
非线性回归模型的线性化 以上介绍了线性回归模型。但有时候变量之间的关系是非线性的。例如 yt = α 0 + α1 + ut β1 t x yt = α 0 + ut t x eα1 上述非线性回归模型是无法用最小二乘法估计参数的。可采用非线性方法进行估计。估 计过程非常复杂和困难，在 20 世纪 40 年代之前几乎不可能实现。计算机的出现大大方便了 非线性回归模型的估计。专用软件使这种计算变得非常容易。但本章不是介绍这类模型的估 计。 另外还有一类非线性回归模型。其形式是非线性的，但可以通过适当的变换，转化为线 性模型，然后利用线性回归模型的估计与检验方法进行处理。称此类模型为可线性化的非线 性模型。下面介绍几种典型的可以做线性化处理的非线性模型。 ⑴ 指数函数模型 yt = (4.1) tt ubx ae + b>0 和 b 0) 图 4.2 yt = , (b 0 和 b<0 两种情形的图形分别见图 4.3 和 4.4。xt 和 yt 的关系是非线性的。令 xt* = Lnxt, 则 yt = a + b xt* + ut (4.5) 变量 yt 和 xt* 已变换成为线性关系。 1

10015020010015020050图4.3,=a+bLnx,+u,(b>0)图4.4y,=a+bLnx,+u,(b10>b>-1100情形的图形见图4.7。x,和y,的关系是非线性的。令y*=1/y,x*=1/x，得y*=a+bx,*+u已变换为线性回归模型。其中u表示随机误差项。2

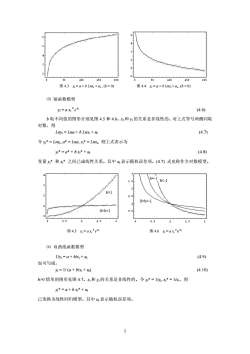
图 4.3 yt = a + b Lnxt + ut , (b > 0) 图 4.4 yt = a + b Lnxt + ut , (b 0 情形的图形见图 4.7。xt 和 yt 的关系是非线性的。令 yt* = 1/yt, xt* = 1/xt，得 yt* = a + b xt* + ut 已变换为线性回归模型。其中 ut 表示随机误差项。 2

1351300.61251200.411511010510000.51.50.51.52.52图4.8y,=a+b/x，图4.7y,=1/(a+b/x,),(b>0)(b > 0)双曲线函数还有另一种表达方式，(4.11)yr= a+ b/x, + utb>0情形的图形见图4.8。x和y的关系是非线性的。令x*=1/x，得y,=a+bx*+u上式已变换成线性回归模型。(5）多项式方程模型一种多项式方程的表达形式是Y= bo +b1x, + b2 x? + b3 x3 + ut(4.12)其中bi>0,bz>0,b>0和bi0,b;0,b2>0和bi<0,b<0情形的图形分别见图4.11和4.12。令x1=x，Xt2=x2，上式线性化为，(4.15)/=bo+bix+b2x+ut如经济学中的边际成本曲线、平均成本曲线与图4.11相似。3

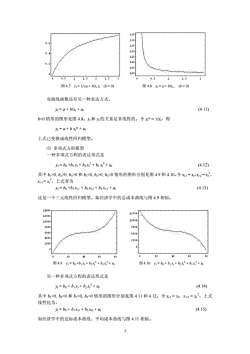
图 4.7 yt = 1/ (a + b/xt ), (b > 0) 图 4.8 yt = a + b/xt , (b > 0) 双曲线函数还有另一种表达方式， yt = a + b/xt + ut (4.11) b>0 情形的图形见图 4.8。xt 和 yt 的关系是非线性的。令 xt* = 1/xt，得 yt = a + b xt* + ut 上式已变换成线性回归模型。 ⑸ 多项式方程模型 一种多项式方程的表达形式是 yt = b0 +b1 xt + b2 xt 2 + b3 xt 3 + ut (4.12) 其中 b1>0, b2>0, b3>0 和 b10, b30, b2>0 和 b1<0, b2<0 情形的图形分别见图 4.11 和 4.12。令 xt 1 = xt，x t 2 = xt 2 ，上式 线性化为， yt = b0 + b1 xt1 + b2 xt2 + ut (4.15) 如经济学中的边际成本曲线、平均成本曲线与图 4.11 相似。 3

16001506014050130401202011020100109010203040104305060405060图4.11 ,=bo+bix,+b2x?+ u图4.12y,=bo+bix,+bax?+u(6）生长曲线（logistic）模型A(4.16)yi=1+e/(0)+m,一般f)=ao+ait+a2t?+...+ant"，常见形式为)=do-atkk(4.17)y=1 +e(aar)+u,I + be -at+n,其中b=e。a0情形的图形分别见图4.13和4.14。美国人口统计学家Pearl和Reed广泛研究了有机体的生长，得到了上述数学模型。生长模型（或逻辑斯谛曲线，Pearl-Reed曲线）常用于描述有机体生长发育过程。其中k和0分别为y的生长上限和下限。Limy，=k,1→oLnbkLimy,=0。a,b为待估参数。曲线有拐点，坐标为（），曲线的上下两部分对称于拐2a1→-2点。k0.80.60.4k/22025301015(Lnb)/a图4.13J,=k/(1+be-at+)图4.14y,=k/(1+be为能运用最小二乘法估计参数a.b，必须事先估计出生曲线长上极限值k。线性化过程如下。当k给出时，作如下变换，kly,=1 + be=af+kly,-1= be-ar+u移项，取自然对数，Ln(klyr-1)=Lnb-at+u(4.18)令y*= Ln(klyr-1),b*=Lnb, 则(4.19)y*=b*-at+ut4

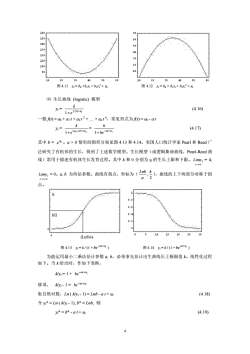
图 4.11 yt = b0 +b1xt + b2xt 2 + ut 图 4.12 yt = b0 + b1xt + b2xt 2 + ut ⑹ 生长曲线 (logistic) 模型 yt = utf t e k + + )( 1 (4.16) 一般 f(t) = a0 + a1 t + a2 t 2 + . + an t n ，常见形式为 f(t) = a0 - a t yt = uata u e k +− + )( 0 1 = uat t be k +− 1+ (4.17) 其中 b = 。a > 0 情形的图形分别见图 4.13 和 4.14。美国人口统计学家 Pearl 和 Reed 广 泛研究了有机体的生长，得到了上述数学模型。生长模型（或逻辑斯谛曲线，Pearl-Reed 曲 线）常用于描述有机体生长发育过程。其中 k 和 0 分别为 yt 的生长上限和下限。 = k, = 0。a, b 为待估参数。曲线有拐点，坐标为（ 0 a e t ∞→ Limyt t −∞→ Limyt a Lnb , 2 k ），曲线的上下两部分对称于拐 点。 图 4.13 yt = k / (1 + ) 图 4.14 yt = k / (1 + ) t uat be +− t uat be + 为能运用最小二乘法估计参数 a, b，必须事先估计出生曲线长上极限值 k。线性化过程 如下。当 k 给出时，作如下变换， k/yt = 1 + t uat be +− 移项， k/yt - 1 = uat t be +− 取自然对数，Ln ( k/yt - 1) = Lnb - a t + ut (4.18) 令 yt* = Ln ( k/yt - 1), b* = Lnb, 则 yt* = b* - a t + ut (4.19) 4

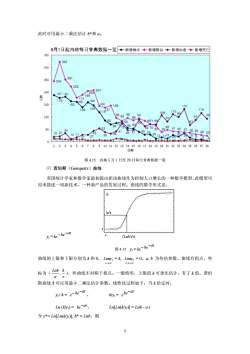
此时可用最小二乘法估计b*和a。5月1日起内地每日非典数据一览→新增确诊→新增似→新增治愈→新增死亡350322300251250244222207200187181189WY17176159160114415016345146103711595584100B0AB62704140R50037352926234464282819.2120710172R17121627054-910111213141516171819202122232425262728日期图4.15内地5月1日至28日每天非典数据一览(7）龚伯斯（Gompertz）曲线英国统计学家和数学家最初提出把该曲线作为控制人口增长的一种数学模型，此模型可用来描述一项新技术，一种新产品的发展过程。曲线的数学形式是，Ekk/eJ,=ke-be-at(Lnb)/a图 4.15 y= ke-be-al曲线的上限和下限分别为k和0，Limy,=k，Limy,=0。a,b为待估参数。曲线有拐点，坐101-→-0标为(Lmb)），但曲线不对称于拐点。一般情形，上限值k可事先估计，有了k值，龚伯a斯曲线才可以用最小二乘法估计参数。线性化过程如下：当k给定时，y/k= e-be-atkly,= ebe-atLn (kly)= be-atLn[Ln(k/y)] = Lnb - a t令y*=Ln[Ln(kly)],b*=Lnb,则5

此时可用最小二乘法估计 b*和 a。 图 4.15 内地 5 月 1 日至 28 日每天非典数据一览 ⑺ 龚伯斯（Gompertz）曲线 英国统计学家和数学家最初提出把该曲线作为控制人口增长的一种数学模型，此模型可 用来描述一项新技术，一种新产品的发展过程。曲线的数学形式是， yt = at be ke − − 图 4.15 yt = at be ke − − 曲线的上限和下限分别为 k 和 0， = k, = 0。a, b 为待估参数。曲线有拐点，坐 标为（ t ∞→ Limyt t −∞→ Limyt a Lnb , e k ），但曲线不对称于拐点。一般情形，上限值 k 可事先估计，有了 k 值，龚伯 斯曲线才可以用最小二乘法估计参数。线性化过程如下：当 k 给定时， yt / k = ， k/yt = at be e − − at be e − Ln (k/yt) = ， Ln[Ln(k/yt)] = Lnb - a t at be− 令 y*= Ln[Ln(k/yt)], b* = Lnb，则 5

y*=b*-at上式可用最小二乘法估计b*和a。Cobb-Douglas生产函数下面介绍柯布-道格拉斯（Cobb-Douglas）生产函数。其形式是Q=kL"cl-a(4.24)其中Q表示产量；L表示劳动力投入量；C表示资本投入量；k是常数；01，称模型为规模报酬递增型；β+β<1，称模型为规模报酬递减型。对于对数线性模型，Lny=Lnβo+βiLnxi+βLnxe+ut，β和β称作弹性系数。以β为例，OLmyt= yr'oyr= y,/yr- Xn oy,βr=(4.28)aLnxoxx,/x,ax可见弹性系数是两个变量的变化率的比。注意，弹性系数是一个无量纲参数，所以便于在不同变量之间比较相应弹性系数的大小。对于线性模型，=+ix+2x+，α和称作边际系数。以α为例，=oyr(4.29)α =axn通过比较（4.28)和（4.29)式，可知线性模型中的回归系数（边际系数）是对数线性回归模型中弹性系数的一个分量。例1：此模型用来评价台湾农业生产效率。用台湾1958-1972年农业生产总值（yl），劳动力（xn），资本投入（xe）数据（见表4.1）为样本得估计模型，Lny,=-3.4 + 1.50 Lnxi + 0.49 Lnx2(4.30)R= 0.89,F= 48.45(2.78)(4.80)还原后得，),= 0.713 x1l50 x0.49(4.31)因为1.50+0.49=1.99，所以，此生产函数属规模报酬递增函数。当劳动力和资本投入都增加1%时，产出增加近2%。6

y* = b* - a t 上式可用最小二乘法估计 b* 和 a。 Cobb-Douglas 生产函数 下面介绍柯布−道格拉斯（Cobb-Douglas）生产函数。其形式是 Q = k Lα C 1- α (4.24) 其中 Q 表示产量；L 表示劳动力投入量；C 表示资本投入量；k 是常数；0 1，称模型为规模报酬递增型； β1 + β2 < 1，称模型为规模报酬递减型。 对于对数线性模型，Lny = Lnβ0 + β1 Lnxt1 + β2 Lnxt2 + ut ，β1 和β2 称作弹性系数。以β1 为例， β1 = t1 t Lnx Lny ∂ ∂ = 1 1 1 1 tt tt xx yy ∂ ∂ − − = 11 / / tt tt xx yy ∂ ∂ = 1 1 t t t t x y y x ∂ ∂ (4.28) 可见弹性系数是两个变量的变化率的比。注意，弹性系数是一个无量纲参数，所以便于在不 同变量之间比较相应弹性系数的大小。 对于线性模型，yt = α0 + α1 xt1 + α2 xt2 + ut ，α1 和 α2 称作边际系数。以α1 为例， α1 = t1 t x y ∂ ∂ (4.29) 通过比较(4.28)和(4.29)式，可知线性模型中的回归系数（边际系数）是对数线性回归模型中 弹性系数的一个分量。 例 1：此模型用来评价台湾农业生产效率。用台湾 1958-1972 年农业生产总值（yt），劳 动力（xt1），资本投入（xt2）数据（见表 4.1）为样本得估计模型， = -3.4 + 1.50 Lnxt1 + 0.49 Lnxt2 (4.30) ∧ Lnyt (2.78) (4.80) R2 = 0.89, F = 48.45 还原后得， = 0.713 xt1 1.50 xt2 0.49 (4.31) t yˆ 因为 1.50 + 0.49 = 1.99，所以，此生产函数属规模报酬递增函数。当劳动力和资本投入都增 加 1%时，产出增加近 2%。 6

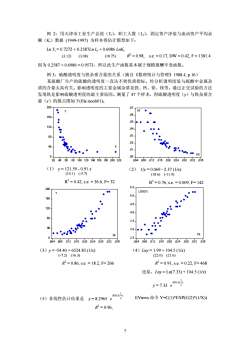
例2：用天津市工业生产总值（Y)，职工人数（L），固定资产净值与流动资产平均余额（K）数据（1949-1997）为样本得估计模型如下：Ln Y,=0.7272 +0.2587Ln L,+0.6986 LnK,R=0.98,S.e.=0.17,DW=0.42,F=1381.4(3.08)(3.12)(18.75)因为0.2587+0.6986=0.9573，所以此生产函数基本属于规模报酬不变函数。例3：硫酸透明度与铁杂质含量的关系（摘自《数理统计与管理》1988.4,p.16）某硫酸厂生产的硫酸的透明度一直达不到优质指标。经分析透明度低与硫酸中金属杂质的含量太高有关。影响透明度的主要金属杂质是铁、钙、铅、镁等。通过正交试验的方法发现铁是影响硫酸透明度的最主要原因。测量了47个样本，得硫酸透明度（y）与铁杂质含量（x）的散点图如下（file:nonlio1)：200.07..1/YY.06160.05120....04..0380".02-40X.01.1K.0020406080100120140160180200220.004.008.012.016.020.024.028032036(1)y=121.59-0.91 x(2)1/y=0.069-2.37(1/x)(10.1)(-5.7)(18.6)(-11.9)R2 = 0.42, s.e. = 36.6, F= 32R2 = 0.76, s.e. = 0.009, F= 1425.5200LOG()00Y5.01604.51204.0803.5403.01k1x2.51004.008.012.016.020024.028.032036.004.008.012.016.020.024.028.032.036(3)y=-54.40+6524.83(1/x)(4) Lmy=1.99 + 104.5 (1/x)(-7.2)(16.3)(22.0)(21.6)R = 0.86, s.e. = 18.2, F= 266R? = 0.91, s.e.=0.22, F= 468还原，Lmy=Ln(7.33)+104.5(1/x)104.5(y=7.33 e100. ()EViews命令Y=C(1)*EXP(C(2)*(1/X)（5）非线性估计结果是y=8.2965eR2 = 0.96,7

例 2：用天津市工业生产总值（Yt），职工人数（Lt），固定资产净值与流动资产平均余 额（Kt）数据 (1949-1997) 为样本得估计模型如下： Ln Yt = 0.7272 + 0.2587Ln Lt + 0.6986 LnKt (3.12) (3.08) (18.75) R2 = 0.98, s.e. = 0.17, DW = 0.42, F = 1381.4 因为 0.2587 + 0.6986 = 0.9573，所以此生产函数基本属于规模报酬不变函数。 例 3：硫酸透明度与铁杂质含量的关系（摘自《数理统计与管理》1988.4, p.16） 某硫酸厂生产的硫酸的透明度一直达不到优质指标。经分析透明度低与硫酸中金属杂 质的含量太高有关。影响透明度的主要金属杂质是铁、钙、铅、镁等。通过正交试验的方法 发现铁是影响硫酸透明度的最主要原因。测量了 47 个样本，得硫酸透明度（y）与铁杂质含 量（x）的散点图如下(file:nonli01)： （1） y = 121.59 - 0.91 x (10.1) (-5.7) R2 = 0.42, s.e. = 36.6, F= 32 （2） 1/y = 0.069 - 2.37 (1/x) (18.6) (-11.9) R2 = 0.76, s.e. = 0.009, F= 142 （3）y = -54.40 + 6524.83 (1/x) (-7.2) (16.3) R2 = 0.86, s.e. = 18.2, F= 266 （4）Lny = 1.99 + 104.5 (1/x) (22.0) (21.6) R2 = 0.91, s.e. = 0.22, F= 468 还原，Lny = Ln(7.33) + 104.5 (1/x) y = 7.33 ) 1 (5.104 x e （5）非线性估计结果是 y = 8.2965 ) 1 (1.100 x e R2 = 0.96, EViews 命令 Y=C(1)*EXP(C(2)*(1/X)) 7

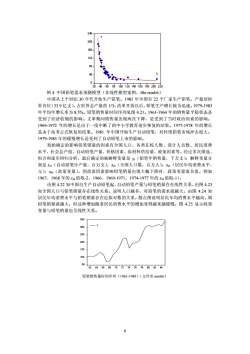
240420016012080X40020406080100120140160180200220例4中国铅笔需求预测模型（非线性模型案例，file:nonli6）中国从上个世纪30年代开始生产铅笔。1985年全国有22个厂家生产铅笔。产量居世界首位（33.9亿支），占世界总产量的1/3。改革开放以后，铅笔生产增长极为迅速。1979-1983年平均年增长率为8.5%。铅笔销售量时间序列见图4.21。1961-1964年的销售量平稳状态是受到了经济收缩的影响。文革期间销售量出现两次下降，是受到了当时政治因素的影响。1969-1972年的增长是由于一度中断了的中小学教育逐步恢复的结果。1977-1978年的增长是由于高考正式恢复的结果。1981年中国开始生产自动铅笔，对传统铅笔市场冲击很大。1979-1985年的缓慢增长是受到了自动铅笔上市的影响。初始确定的影响铅笔销量的因素有全国人口、各类在校人数、设计人员数、居民消费水平、社会总产值、自动铅笔产量、价格因素、原材料供给量、政策因素等。经过多次筛选、组合和逐步回归分析，最后确定的被解释变量是（铅笔年销售量，千万支）；解释变量分别是x（自动铅笔年产量，百万支）：x2（全国人口数，百万人）：xs（居民年均消费水平，元）；x4（政策变量）。因政策因素影响铅笔销量出现大幅下降时，政策变量取负值。例如1967、1968年的x4值取-2，1966、1969-1971、1974-1977年的x4值取-1)。由图4.22知中国自生产自动铅笔起，自动铅笔产量与铅笔销量存在线性关系。由图4.23知全国人口与铅笔销量存在线性关系。说明人口越多，对铅笔的需求就越大。由图4.24知居民年均消费水平与铅笔销量存在近似对数的关系。散点图说明居民年均消费水平越高，则铅笔销量就越大。但这种增加随着居民消费水平的增加变得越来越缓慢。图4.25显示政策变量与铅笔销量也呈线性关系。35030025020015010050626466687072747678808284铅笔销售量时间序列（1961-1985）（文件名nonli6）8

例 4 中国铅笔需求预测模型（非线性模型案例，file:nonli6） 中国从上个世纪 30 年代开始生产铅笔。1985 年全国有 22 个厂家生产铅笔。产量居世 界首位（33.9 亿支），占世界总产量的 1/3。改革开放以后，铅笔生产增长极为迅速。1979-1983 年平均年增长率为 8.5%。铅笔销售量时间序列见图 4.21。1961-1964 年的销售量平稳状态是 受到了经济收缩的影响。文革期间销售量出现两次下降，是受到了当时政治因素的影响。 1969-1972 年的增长是由于一度中断了的中小学教育逐步恢复的结果。1977-1978 年的增长 是由于高考正式恢复的结果。1981 年中国开始生产自动铅笔，对传统铅笔市场冲击很大。 1979-1985 年的缓慢增长是受到了自动铅笔上市的影响。 初始确定的影响铅笔销量的因素有全国人口、各类在校人数、设计人员数、居民消费 水平、社会总产值、自动铅笔产量、价格因素、原材料供给量、政策因素等。经过多次筛选、 组合和逐步回归分析，最后确定的被解释变量是 yt（铅笔年销售量，千万支）；解释变量分 别是 xt1（自动铅笔年产量，百万支）；xt2（全国人口数，百万人）；xt3（居民年均消费水平， 元）；xt4（政策变量）。因政策因素影响铅笔销量出现大幅下降时，政策变量取负值。例如 1967、1968 年的 xt4 值取-2，1966、1969-1971、1974-1977 年的 xt4 值取-1）。 由图 4.22 知中国自生产自动铅笔起，自动铅笔产量与铅笔销量存在线性关系。由图 4.23 知全国人口与铅笔销量存在线性关系。说明人口越多，对铅笔的需求就越大。由图 4.24 知 居民年均消费水平与铅笔销量存在近似对数的关系。散点图说明居民年均消费水平越高，则 铅笔销量就越大。但这种增加随着居民消费水平的增加变得越来越缓慢。图 4.25 显示政策 变量与铅笔销量也呈线性关系。 50 100 150 200 250 300 350 62 64 66 68 70 72 74 76 78 80 82 84 Y 铅笔销售量时间序列（1961-1985）（文件名 nonli6） 8

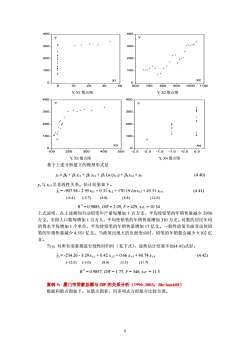
40Y:300-300 Io200.200:*..100100:X2X10001020304060070080090010001100Y,XI散点图Y,X2散点图400400YY3003004200200-.......:100100"X3X40-0-200400-2.0100300500-2.5-1.5-1.0-0.50.0Y,X3散点图Y,X4散点图基于上述分析建立的模型形式是(4.40)y=Bo+Bix+BX12+βLn(xr3)+B4x14+utJ与x3呈非线性关系。估计结果如下。j,=-907.94-2.95x1+0.31 xi2+170.19 Ln Xx3+45.51 x14(4.41)(-3.7)(4.8)(4.4)(12.6)(-6.4)R2=0.9885,DW=2.09,F=429,s.e.=10.34上式说明，在上述期间自动铅笔年产量每增加1百万支，平均使铅笔的年销售量减少2950万支。全国人口数每增加1百万人，平均使铅笔的年销售量增加310万支。对数的居民年均消费水平每增加1个单位，平均使铅笔的年销售量增加17亿支。一般性政策负面变动使铅笔的年销售量减少4.551亿支。当政策出现大的负面变动时，铅笔的年销量会减少9.102亿支。当yt对所有变量都进行线性回归时（见下式），显然估计结果不如(4.41)式好。(4.42)j,= -254.26- 3.29x1 + 0.42 xt2 + 0.66x±3 + 40.74 x/4(-12.0)(-3.0)(8.6)(3.5)(11.7)R?=0.9857,DW= 1.77, F= 346, s.e.=11.5案例5：厦门市贷款总额与GDP的关系分析（1990-2003，file:bank08）数据和散点图如下。从散点图看，用多项式方程拟合比较合理。9

0 100 200 300 400 0 10 20 30 40 X1 Y 0 100 200 300 400 600 700 800 900 1000 1100 X2 Y Y, X1 散点图 Y, X2 散点图 0 100 200 300 400 100 200 300 400 500 X3 Y 0 100 200 300 400 -2.5 -2.0 -1.5 -1.0 -0.5 0.0 X4 Y Y, X3 散点图 Y, X4 散点图 基于上述分析建立的模型形式是 yt = β0 + β1 xt 1 + β2 xt 2 + β3 Ln (xt 3) + β4 xt 4 + ut (4.40) yt 与 xt 3 呈非线性关系。估计结果如下。 = -907.94 - 2.95 xt 1 + 0.31 xt 2 + 170.19 Ln xt 3 + 45.51 xt 4 (4.41) t yˆ (-6.4) (-3.7) (4.8) (4.4) (12.6) R 2 = 0.9885, DW = 2.09, F = 429, s.e. = 10.34 上式说明，在上述期间自动铅笔年产量每增加 1 百万支，平均使铅笔的年销售量减少 2950 万支。全国人口数每增加 1 百万人，平均使铅笔的年销售量增加 310 万支。对数的居民年均 消费水平每增加 1 个单位，平均使铅笔的年销售量增加 17 亿支。一般性政策负面变动使铅 笔的年销售量减少 4.551 亿支。当政策出现大的负面变动时，铅笔的年销量会减少 9.102 亿 支。 当 yt 对所有变量都进行线性回归时（见下式），显然估计结果不如(4.41)式好。 = -254.26 - 3.29 x t 1 + 0.42 x t 2 + 0.66 x t 3 + 40.74 x t 4 (4.42) t yˆ (-12.0) (-3.0) (8.6) (3.5) (11.7) R 2 = 0.9857, DW = 1.77, F = 346, s.e. = 11.5 案例 5：厦门市贷款总额与 GDP 的关系分析（1990~2003，file:bank08） 数据和散点图如下。从散点图看，用多项式方程拟合比较合理。 9

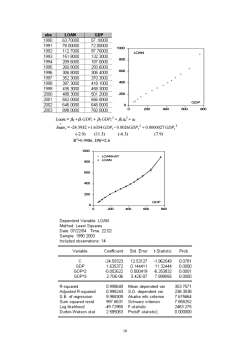
GDPobsLOAN199063.7000057.10000199178.0000072.0000010001992112.700097.70000LOAN1993151.8000132.30008001994209.6000187.00001995260.8000250.60006001996306.8000306.40001997352.3000370.30004001998397.3000418.10001999435.3000458.30002000200488.3000501.20002001552.0000556.0000GDP2002of646.0000648.000002004006008002003898.0000760.0000Loan,=βo+βiGDP,+βGDP,2+βx+uloan,=-24.5932+1.6354GDP,-0.0026GDP2+0.0000027GDP3(-2.0)(-6.3)(7.9)(11.3)R*=0.9986, DW=2.61000LOANHATLOAN4800600400200KGDPo+2004006000800DependentVariable:LOANMethod: Least SquaresDate:07/22/04Time:22:02Sample: 1990 2003Includedobservations:14Std. ErrorProb.VariableCoefficientt-StatisticC-24.5932312.53127-1.9625490.0781GDP1.6353720.14441111.324440.0000GDP^2-0.0026220.0004190.0001-6.253832GDPA30.00002.70E-063.42E-077.899055R-squared353.75710.998649Mean dependent var0.998243238.3038Adjusted R-squaredS.D. dependent var9.9883097.675664S.E. of regressionAkaike info criterion997.66317.858252Sum squared residSchwarz criterion-49.729652463.275Log likelihoodF-statistic2.585063Prob(F-statistic)0.000000Durbin-Watson stat10

0 200 400 600 800 1000 0 200 400 600 800 GDP LOAN Loant = β0 +β1 GDPt + β2 GDPt 2 + β3 xt 3 + ut ∧ loan t = -24.5932 +1.6354 GDPt - 0.0026GDPt 2 + 0.0000027 GDPt 3 (-2.0) (11.3) (-6.3) (7.9) R2 =0.9986, DW=2.6 0 200 400 600 800 1000 0 200 400 600 800 GDP LOANHAT LOAN 10