《复变函数与积分变换》课程教学课件（讲稿）1-1-1复数的概念

复数的概念与计算

复数的概念与计算

第一讲 复数的概念

第一讲 复数的概念

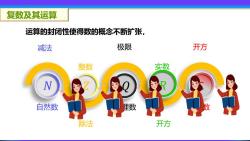
复数及其运算 运算的封闭性使得数的概念不断扩张， 减法 极限 开方 整数 实数 N 自然数 里数 数 除法 开方

自然数 实数 复数 减法 极限 开方 除法 开方 𝑁 整数 𝑍 有理数 𝑄 𝑅 C 运算的封闭性使得数的概念不断扩张， 复数及其运算

？2=-1 或v-1=?

？2 =−1 或 −1 = ？

1、虚单位 虚单位：i=V一1， 2=-1,3=-i,4=1: 一般地，k∈Z i4k=1,i4k+1=i,i4k+2=-1,i4k+3=-i;

虚单位：𝑖 = −1 ， 一般地，𝐤 ∈ 𝒁 𝑖 2 = −1, 𝑖 3 = −𝑖, 𝑖 4 = 1 ; 𝑖 4𝑘 = 1, 𝑖 4𝑘+1 = 𝑖, 𝑖 4𝑘+2 = −1, 𝑖 4𝑘+3 = −𝑖 ; 1、虚单位

基础练习 20=1 20÷4=5 i4k=1 2003 :-i 2000÷4=500 3=-i 2022=-1 2020÷4=505 2=-1 i1997=i 1996÷4=499 V-9=3i 9xV-1 i=V-1 V-2=V2i 2×V-1

基础练习 𝑖 20 = _; 𝑖 2022 = _; 𝑖 2003 = _; 𝑖 1997 = _; −9 = _; −2 = _; 1 −1 3𝑖 −𝑖 𝑖 2𝑖 20 ÷ 4 = 5 𝑖 4𝑘 = 1 2000 ÷ 4 = 500 𝑖 3 = −𝑖 2020 ÷ 4 = 505 𝑖 2 = −1 1996 ÷ 4 = 499 𝑖 9 × −1 𝑖= −1 2 × −1

2.复数 复数形如z=x+iy或x+yi(x,yER)。 复数z的实部记为Re(z)=x，R-全体实数集 复数z的虚部记为Im(z)=y, 实数可看作复数x=x+0因此RcC, 纯虚数是复数：yi=0+yiy≠0.C-全体复数集

2.复数 复数形如 𝒛 = 𝒙 + 𝒊𝒚或𝒙 + 𝒚𝒊(𝒙, 𝒚 ∈ 𝑹) 。 复数𝒛的虚部记为𝑰𝒎 𝒛 = 𝒚 ， 实数可看作复数 𝒙 = 𝒙 + 𝒊𝟎 因此𝑹 ⊂ 𝑪， 纯虚数是复数：𝒚𝒊 = 𝟎 + 𝒚𝒊 𝒚 ≠ 𝟎. 复数𝒛的实部记为𝑹𝒆 𝒛 = 𝒙 ， 𝑹-全体实数集 𝑪-全体复数集

基础练习 (1)2-3的实部是（2)，虚部是（-3)。 (2)-6i的实部是（0)，虚部是（-6)

(1) 2 − 3𝑖的实部是（ ），虚部是（ ）。 (2) −6𝑖 的实部是（ ），虚部是（ ）。 2 −3 0 −6 基础练习

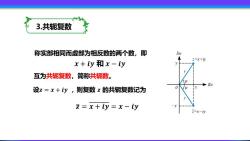
3.共轭复数 称实部相同而虚部为相反数的两个数，即 Im E=x+iy x+y和x-y 互为共轭复数，简称共轭数。 Re 设z=x+y,则复数z的共轭复数记为 Z=x+iy=x-iy =x-iv

3.共轭复数 称实部相同而虚部为相反数的两个数，即 互为共轭复数，简称共轭数。 设𝒛 = 𝒙 + 𝒊𝒚 ，则复数 𝒛 的共轭复数记为 𝒙 + 𝒊𝒚 和 𝒙 − 𝒊𝒚 𝒛 = 𝒙 + 𝒊𝒚 = 𝒙 − 𝒊𝒚

基础练习 (1)2-3的共轭复数是（2+3i)。 (2)6i-7的共轭复数是(-7-6i)

基础练习 (1) 2 − 3𝑖的共轭复数是（ ）。 (2) 6𝑖 − 7 的共轭复数是( ）。 2 + 3𝑖 −7 − 6𝑖