《高等数学》课程教学课件（讲稿）12-6-2一般周期函数的傅里叶级数2/2

第六讲 有限区间函数的傅里叶级数

无 穷 级 数 第六讲 有限区间函数的傅里叶级数

无穷级数 1.任意有限区间函数的傅里叶级数 方法1fx),x∈[ab] 令x=z+,即z=x- b+a 2 F=f=f(a+20）,ze2, 周期延拓 F2)在“2，上展成傅里叶级数 将2=x-代入展开式 f(x)在[a,b]上的傅里叶级数

无 穷 级 数 1. 任意有限区间函数的傅里叶级数 方法1 ᵈ(ᵉ ) ,  ᵉ ∈ [ᵈ ,ᵈ ] 即 周期延拓

无穷级数 方法2fx),x∈[ab] 令x=z+a,即 z=x-a F(z)=f(x)=f(z+a), z∈[0，b-a 奇或偶式周期延拓 F(z)在[0，b-a]上展成正弦或余弦级数 将z=x一a代入展开式 f(x)在[a,b]上的正弦或余弦级数

无 穷 级 数 方法2 ᵈ(ᵉ ) ,   ᵉ ∈ [ᵈ ,ᵈ ] 令ᵉ = ᵉ + ᵈ , ᵆ (ᵉ) = ᵈ(ᵉ ) = ᵈ(ᵉ + ᵈ ),   奇或偶式周期延拓 即 ᵉ = ᵉ − ᵈ

无穷级数 举例 例1：将函数f(x)=10-5x(5<x<15) 展开成傅里叶级数，并作出级数的和函数图形 解：令z=x-10,设F(z)=f(x)=f(z+10)=-z,z∈(-5,5) 将F(z)延拓成周期为10的周期函数，则它满足收敛定 理条件.由于F(z)是奇函数，an=0(n∈N) F(Z) ba=专-zstm"gdz=(-19 00 10(-1)” mπz F(Z)= -sin- π台 (-5<z<5) n 5 (n=1,2,.) 10(-1)” nπx ·10-5x= sin (5<X<15) n n1

无 穷 级 数 举例 展开成傅里叶级数，并作出级数的和函数图形. ᵃ (ᵆ ) 5 ᵆ − 5 解: 令ᵉ = ᵉ − ᵼᵼ , 理条件. (ᵅ = 1 , 2,  ⋯ ) 则它满足收敛定 (−5 < ᵆ < 5) (5 < ᵆ < 15)

无穷级敛 2.傅里叶级数的复数形式 设f(x)是周期为2的周期函数，则 九πx nπx f(x (ancos+basin n=1 nπx cos e贤+e 2 利用欧拉公式 =(e贤-e nπx 00 f(x)= 2+I2a晋+e)(e7-。受】 2 n=1 00 ao 2 an-iono+amibe 2 2 n=1 C-

无 穷 级 数 2. 傅里叶级数的复数形式 利用欧拉公式 ᵈ ᵼ ᵈ ᵈ

无穷级敛 注意到co==,f)dx cn=,=」fx)cos"dx-号)sin"贤dx =oc"-n"7）a。平 =fe学dxm=1,2) 同理cn=7厂e7dxa=12

无 穷 级 数 注意到 同理

无穷级数 因此得傅里叶级数的复数形式： 十0 f(x)= ∑ae n=-0o ∫=fwe呼ax n=0,±1，±2，.）

无 穷 级 数 因此得傅里叶级数的复数形式: (ᵈ = ᵼ ,± ᵼ ,± ᵽ , ⋯ )

无穷级数 举例 例2.把宽为τ，高为h,周期为T的矩形波展成 复数形式的傅里叶级数. 解：在一个周期 引 h 内矩形波的函数表达式为 u(t)= 了h,-i≤t<月 0,-≤t<-i,st< T 它的复数形式的傅里叶系数为 co=度u(因dt=度ndt=凭

无 穷 级 数 举例 复数形式的傅里叶级数 . 解: 在一个周期 ᵉ (ᵉ) = 它的复数形式的傅里叶系数为 内矩形波的函数表达式为 − ᵴ ᵽ ᵇ ᵽ ᵅ ᵉ ᵉ ᵴ ᵽ − ᵇ ᵽ ᵈ

无穷级敛 2nπt -。学。引e-e学] h sin T nπ (n=±1，±2，.) +00 ht h 1.nπt2nπ .u(t)= >sin T -e T n≠0 (t≠+，k=0,±1，.) 2

无 穷 级 数 (ᵈ = ±ᵼ  , ±ᵽ  ,  ⋯  ) (ᵉ ≠ ± ᵴ ᵽ + ᵈᵇ , ᵈ = ᵼ , ± ᵼ ,  ⋯ )

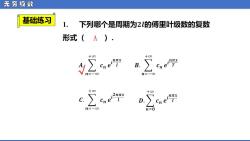
无穷级敛 基础练习 1. 下列哪个是周期为2的傅里叶级数的复数 形式（A). +00 +00 nπx Cne n=-0o 十00 i2nnx +00 nπx D n=-00 n=0

无 穷 级 数 基础练习 √ A