《高等数学》课程教学课件（讲稿）12-5-4傅里叶级数的计算3/3奇偶延拓

第四讲 傅里叶级数的计算

无 穷 级 数 第四讲 傅里叶级数的计算

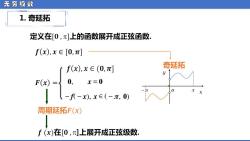
无穷级数 1.奇延拓 定义在[0，π上的函数展开成正弦函数 f(x),x∈[0，π] ff(x),x∈(0，π] 奇延拓 F()= 0, x=0 1-x-x0 周期延拓F(x) f(x)在[0，]上展开成正弦级数

无 穷 级 数 1. 奇延拓 奇延拓 ᵆ ᵅ ᵰ ᵆ − ᵰ ᵼ ,  ᵉ = ᵼ − ᵈ( − ᵉ ), ᵉ ∈ ( − ᵴ , ᵼ )

无穷级数 2.偶延拓 定义在[0，π]上的函数展开成余弦函数 f(x),x∈[0，π] 偶延拓 (f(x),x∈(0，π] F(x)= -,xe-x0 周期延拓F(x) f(x)在[0，上展开成余弦级数

无 穷 级 数 2. 偶延拓 偶延拓 ᵈ( − ᵉ ), ᵉ ∈ ( − ᵴ , ᵼ ) − ᵰ ᵅ ᵰ ᵆ ᵆ

无穷级数 举例 例1：将函数f(x)=x+1,x∈[0，π]分别展开成 余弦与正弦级数， 解：先求正弦级数.去掉端点，将f(x)作奇周期延拓， nf)sinnxdx +1)sinnxdx xcosnx sinnx cognx n n =2(1-πcosnm-cosnπ) nπ

无 穷 级 数 举例 1 ᵰ ᵆ ᵆ ᵅ 解: 先求正弦级数.去掉端点, 将 f (x) 作奇周期延拓, − ᵰ

无穷级数 bn=2[1-(-1)"π-(-1)n则 nπ 2 π+2 π 2k-1'n=2k-1 (k=1,2,. n=2k 因此得 x+1=引π+2)smx-受sn2+" 3 sin3x π sin4x+.](0<x<m) 注意：在端点x= 0,π，级数的和为0，与给定函数 f(x)=x+1的值不同

无 穷 级 数 = ᵈ = ᵽ ᵈ − ᵼ (ᵈ = ᵼ , ᵽ ,  ⋯ ) (ᵼ < ᵉ < ᵴ ) 因此得 注意: 与给定函数 1 ᵰ ᵆ ᵆ − ᵰ ᵅ

无穷级数 再求余弦级数.将f(x)作偶周期延拓，则有 a,=是0x+10dx=2（(管+x)=x+2 a=(x+1)cosnxdx [ x sinnx cos nx sinnx n n2 2 n2 -(cosnπ-1) 4 (2k-1)2元， n=2k-1 (k=1,2,.) 0 n 2k

无 穷 级 数 再求余弦级数. ᵰ ᵆ 1 ᵆ 则有 ᵰ ᵅ ᵈ ᵼ = ᵈ ᵈ = = ᵴ + ᵽ (ᵈ = ᵼ , ᵽ , ⋯ ) 作偶周期延拓

无穷级数 因此得 x+1= +1-4 1 π名(2k-1)2cos(2k-1)x -+1cosx+os3x+ 1 1 2c0s5x+.] 说明：令x=0可得 (0≤x≤π) π2 1+ 5+.= 1 32 8 即 1 π2 (2k-1)2 =8

无 穷 级 数 因此得 (ᵼ ≤ ᵉ ≤ ᵴ ) 即

无穷级敛 基础练习 1.在[0，口上的函数的傅里叶展开法唯一吗？ 答：不唯一，延拓方式不同级数就不同 在[0，口上函数的傅里叶展开法 ·作奇周期延拓，展开为正弦级数 ·作偶周期延拓，展开为余弦级数

无 穷 级 数 基础练习 1. 在 [ 0 , ᵆ ] 上的函数的傅里叶展开法唯一吗? 答: 不唯一 , 延拓方式不同级数就不同 . 在 [ 0 , ᵆ ] 上函数的傅里叶展开法 • 作奇周期延拓 , 展开为正弦级数 • 作偶周期延拓 , 展开为余弦级数

无穷级数 基础练习 2. 设周期函数在一个周期内的表达式为 -1,-π<x≤0 fx)- 1+x2,0<X≤π 0 1x 则它的傅里叶级数在x=π处收敛于 在x=4π处收敛于 0 提示 f(π)+f(π 2=f)-m）= 2 2 f4π)+f4r）=f0)+f(0)=-1+1 2 2 2

无 穷 级 数 基础练习 ᵅ(ᵆ ) = 提示: 2. 设周期函数在一个周期内的表达式为 − ᵰ ᵆ ᵆ ᵅ ᵰ − 1 1 0

无穷级敛 基础练习 -1, -π<X<0 3.写出函数p= 在[-π，x]上 0≤X≤元 傅氏级数的和函数. -1, -元<X<0 答案：SX)=〈 1, 0<X<π fx) 0, X=0 0. X=土元

无 穷 级 数 基础练习 3. 写出函数ᵆ(ᵆ)= − 1,  − ᵰ < ᵆ < 0 1,     0 ≤ ᵆ ≤ ᵰ 在 [ − ᵴ , ᵴ ] 上 傅氏级数的和函数 . ᵄ (ᵆ ) = − 1,  − ᵰ < ᵆ < 0 1,   0 < ᵆ < ᵰ 0, ᵆ = 0 0, ᵆ = ±ᵰ 答案: − ᵰ ᵆ ᵆ ᵅ ᵰ − 1 1 ᵅ(ᵆ )