《高等数学》课程教学课件（讲稿）12-2-1正项级数的审敛法

第四讲 正项级数及其收敛法

无 穷 级 数 第四讲 正项级数及其收敛法

无穷级数 1.正项级数的审敛性 0∞ 定义1.若un≥0，则级数 )un称为正项级数！ 00 n=1 定理1.正项级数 1 n收敛≤部分和序列Sn(n=1,2,.)有界. n=1 00 证：→若级数 〉un收敛， 则部分和数列{Sn}收敛，故{Sn}有界， n=1 ←一：un≥0，部分和数列{Sn}单调递增，又已知{Sn}有界， 00 故{Sn收敛，从而>un收敛 n=1

无 穷 级 数 1.正项级数的审敛性 则级数 定理1.正项级数 证:

无穷级数 00 定理2.（比较审敛法）设4， vn是两个正项级数， n=1 m.=1 un≤vn(n=1,2,.) 00 (1)若”大“级数〉vn收敛，则"小"级数也) un收敛. n=1 n=1 00 00 (2)若”小“级数∑um发散，则“大“级数也) vn发散。 n=1 n=1

无 穷 级 数 定理2. (比较审敛法) 设

无穷级数 举例 1 例1.判定级数 的敛散性， n=ivn(n+1) 1 1 1 解：“Vnn+万>m+1m+面 n+1 因为级数 1 发散，所以级数 n+1 n=1 1 一也发散

无 穷 级 数 举例 例1. 判定级数 的敛散性. 解： 所以级数

无穷级数 00 推论.（比较审敛法）设 ∑，∑ n是两个正项级数，且存在 n=1 n=1 正整数N,使得当n≥N时，un≤kvn(k>0)成立， (1)若”强“级数)un收敛，则"弱"级数∑也收敛. n=1 n=1 (2)若”弱“级数 un发散，则“强"级数 vn也发散. n=1 n=1

无 穷 级 数 推论. (比较审敛法) 设

无穷级敛 0 00 定理3.（比较审敛法的积项形式）设〉 Un, vn是两个正项级数， m=1 n=1 若m=L, n-0 Vn 00 00 (1)为有限非零常数，则级数 un同为敛散性. n=1 n=1 00 00 (2=0,若级数vn收敛，则级数 ∑ un收敛， n=1 n=1 00 00 (3)1=+∞，若级数 )1 n发散，则级数 un发散 n=1 n=1 看分母级数的敛散性

无 穷 级 数 定理3. (比较审敛法的积项形式) 设 (ᵽ )ᵈ = ᵼ ， (ᵽ )ᵈ = + ∞， 看分母级数的敛散性

无穷级数 2. p级数的敛散性 例1.讨论刀级数1++品++.（常数刀>0）的敛散性 解：(1)若p≤1，因为对-切n∈z,≥是 00 而调和级数 发散，由比较审敛法可知p级数 n=1 品+品+品+.（常数p≤1）发散。 1+

无 穷 级 数 解: 而调和级数

无穷级敛 2若都>1，因为当k-1三x三k有忘≤日 1 所以后-心品4≤品a=23） 5,=+2e1+a“=1+品x =1*,1-)）收敛 2

无 穷 级 数 所以

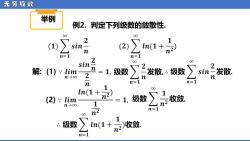
无穷级数 举例 例2.判定下列级数的敛散性 00 2 (1) sin- (2) 台 n=1 1+是 00 sin 00 二发撒六级数 2 解：(1)lim =1,级数 sin- 发散 n→0∞ 2 n n=1 n=1 1 (2)lim m(1+n2) 1,级数 收敛， n→o 1 m=1 00 n2 1 级数 合 +是收敛

无 穷 级 数 举例 例2. 判定下列级数的敛散性. 解:

无穷级敛 基础练习 1. 下列哪个级数是收敛的？ (D) 1 A. √n(n+2) 00 1 B sin- C. 00 1+n 1+n3

无 穷 级 数 基础练习 1. 下列哪个级数是收敛的？ √ (ᵆ )