《高等数学》课程教学课件（讲稿）12-5-1傅里叶级数

第一讲 傅里叶级数的概念

无 穷 级 数 第一讲 傅里叶级数的概念

1112 10 2 9 8 6 5

无 穷 级 数

无 穷 级 数

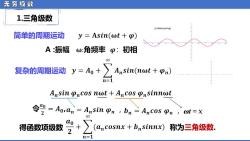
无穷级数 1.三角级数 y=Asin(ut+p)】 简单的周期运动 y=Asin(ωt+p) A振幅ω：角频率 p:初相 00 复杂的周期运动y=A0+∑Ansin(wt+pn) n=1 Ansin pncos nut Ancos pnsinnut 令2=A,an=Ansin Pr,bn≥Ancos n,f=X 得函数项级数 受+∑a,.cOSnX+b,sdnm)称为三角级数 n=1

无 穷 级 数 1.三角级数 简单的周期运动 复杂的周期运动 ᵴ ᵉ = ᵆ 得函数项级数 称为三角级数

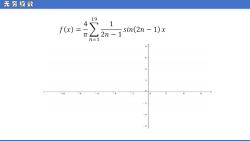
无穷级数 19 f)=4 1 sin(2n-1)x 2n-1 n=1 4 2 -6

无 穷 级 数

无穷级数 2.三角函数系的正交性 定理1：组成三角级数的函数系 1,cosx,sinx,cos2x,sin2x,.,cosnx,sinnx,. 在[-π，π]上正交，即其中任意两个不同的函数之积，在 [-π，π]上积分为0. ∫cosnxdx=0(m∈Zt+),"sinnxdx=0(n∈Z+) "sinkxcosnxdx=0(k,nZ+) ∫coskxcosnxdx=0(k,n∈Z+,k≠n) sinkxsinnxdx=0(k,n∈Z+,k≠n)

无 穷 级 数 定理1：组成三角级数的函数系 2.三角函数系的正交性

无穷级数 但是在三角函数系中两个相同的函数的乘积在[一π，π] 上的积分不等于0. ∫ndx=2m, ∫nc0s2nxdx=π，→cos2nx= 1+cos2nx 2 ∫nsin2nxdx=元， sin2nx=1-cos2nx 2

无 穷 级 数

无穷级数 3.函数展开成傅里叶级数 定理2：设f(x)是周期为2π的周期函数，且 f0w-受+a.CO+b.stnm因 ● n=1 右端级数可逐项积分，则有 au=是Jnfx)cosnxdx (n=0,1,2.) bnf(x)sinnxdx (n=1,2,.)

无 穷 级 数 右端级数可逐项积分, 则有 3.函数展开成傅里叶级数

无穷级数 证：由定理条件，对函数f(x)两端在[-π，π上积分： sinnxdx) -元 n=1 -元 fx)dx=a→ao=元fxdx 元 对函数f(x)两端同乘c0skx,在[-π，π]上积分： f(x)coskxdx= 0 coskxdx+ 2 ∑(au∫coskxcosnxdx+b coskxsinnxdx) 2

无 穷 级 数 ⟹

无穷级数 当k=n时， (k≠n时左端积分为0，利用正交性) an=t」f()cosnxdx (n=1,2.), 对函数f(x)两端同乘sinkx,在[-L,π]上积分： 当k=n时，(k≠n时左端积分为0，利用正交性) bn=」nfx)sinnxdx (n=1,2,.). an,bn称为函数f(x)的傅里叶系数，以傅里叶系数为系数的 级数称为傅里叶级数

无 穷 级 数