《高等数学》课程教学课件（讲稿）12-6-1一般周期函数的傅里叶级数1/2

第五讲 周期为2L的周期函数 的傅里叶级数

无 穷 级 数 第五讲 周期为2L的周期函数 的傅里叶级数

无穷级数 1.周期为2L的周期函数的傅里叶级数 周期为2l函数f(x) 当-L≤x≤l时， 变量代换z= πX πX 两端同乘得，一π≤ ≤π 周期为2π函数F(z) -π≤z≤π 将F(Z)作傅氏展开 f(x)的傅氏展开式

无 穷 级 数 变量代换 − ᵴ ≤ ᵉ ≤ ᵴ ᵴ ᵈ

无穷级数 定理1.设周期为2L的周期函数f(x)满足收敛定理条件 则它的傅里叶展开式为 f-2+aosn+,sm"7) nπx (在f(x)的连续点处) 其中 an=if f(x)cosdx n=0.1.2. Cbn=广f)sin"dx n=1,2

无 穷 级 数 则它的傅里叶展开式为 其中

无穷级数 证明：令z=7 X 则-l≤x≤l,变换成-π≤z≤π. f(x)=f(=F(z),F(z)周期为2π，且满足收敛定理条件. 将它展成傅里叶级数： P F(A)=(an cosnz+bsinnz) 2 n=1 (在F(z)的连续点处) 其中 an=F(z)cosnzdzn0.1.2. b=∫nra)sinnzdz n=1,2

无 穷 级 数 证明: 令 将它展成傅里叶级数: 其中

无穷级数 a:=F(②cosnzdzn=0,12 bn =1F()sinnzdz n=1.2. |z=代换 an=iff()cosdx n=0.1,2. n=if()sindx n=1.2. f-2+∑acos"+bsm"t） nπx n=1 (在f(x)的连续点处)

无 穷 级 数

无穷级敛 说明：如果f(x)为奇函数，则有 -an=0,n=0,1,2. bn=是fx)sindx,n=1,2 如果f(x)为偶函数，则有 ram=号6fx)cos%tdxn=01,2. bm=0,n=1,2. 注：无论哪种情况，在f(x)的间断点x处，傅里叶级数 收敛于fx)+fx刀

无 穷 级 数 说明: 注: 无论哪种情况 , ᵼ ᵽ [ᵈ( ᵉ − ) + ᵈ( ᵉ + 收敛于 )]

无穷级数 举例 例1：把以4为周期的函数f(,)= 0,-2≤x<0 1h,0≤x<2 常数≠0，展开成傅里叶级数，并作出级数的和函数图形. 解：l=2,a0=2」2fx)dx=26hdx=h: an=ihcos"dx=12. Dnhsin dx h nπx2_h -COS- 2 [1-(-1)"] nπ 00 h 1 (2n-1)πx f(x)= 2+π 十 sin /2n-1 2 ’(x∈R,x≠2k,k∈Z) n=]

无 穷 级 数 举例 ℎ 2 ᵆ ᵆ ᵅ

无穷级数 举例 例2：把函数f(x)=x(0<x<2)展开成 (1)正弦级数 (2)余弦级数 解：（1)l=2,将函数奇延拓an=0; b=26xsindx,n=1,2 2 nπx 2 2 2 n -xCOS- -dx n 2 0 nπJ0 在x=2k处级 -C0Snπ= (-1)n+1 nπ nπ 数收敛于何值？ 00 4 (-1)n+1 nπx f(x)= sin (0<x<2) 2

无 穷 级 数 举例 (1)正弦级数 （2）余弦级数 (0 < ᵆ < 2) 2 ᵅ ᵆ ᵆ 0

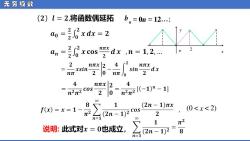
无穷级数 (2)1=2,将函数偶延 ib =On =12. ao=xdx=2 n32 xcos"空dx,n=1,2. 2 xnnπx2_4 nπ xsin- nπ 20nπJo sin 2 dx 4 nπX 2 4 n2π2cos2 n2m2-1)m-1] ●X G)1(m-1c0s 8 2n-1)πx ,(0<x<2) 2 说眼：对x=0他威立。 1 π2 4(2n-102=8

无 穷 级 数 2 ᵅ ᵆ ᵆ (0 < ᵆ < 2) ᵈ ᵈ = ᵼ ,ᵈ = ᵼ ,ᵽ .;

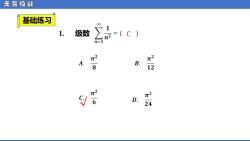
无穷级敛 基础练习 1.级数 -(c) π2 A. B. 12 √ D. 24

无 穷 级 数 基础练习 1. 级数 √ C