《复变函数与积分变换》课程教学课件（讲稿）1-3-1平面点集

复数与复变函数

复数与复变函数

第六讲 平面点来

第六讲 平面点集

平面点集 1.邻域 平面上以z0为中心，6(/6>0)为半径的开圆表示为： |z-zo1<6,称为zo的邻域。 不等式0<|z-zo<δ，确定的点集，称为z0的去心邻域

平面点集 1.邻域

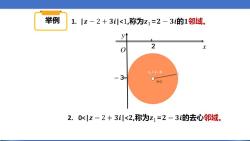
举例 1.|z-2+3川<1，称为z1=2-3的1邻域。 2 2=2-3 -3 6=2 2.0<|z-2+3川<2，称为z1=2-3的去心邻域

举例 ᵆ ᵆᵄ 2 − 3

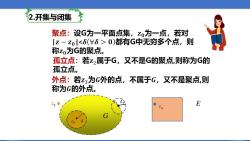
2.开集与闭集 聚点：设G为一平面点集，z0为一点，若对 |z-z0|0)都有G中无穷多个点，则 称zo为G的聚点。 孤立点：若z2属于G,又不是G的聚点，则称为G的 孤立点。 外点：若23为G外的点，不属于G,又不是聚点则 称为G的外点。 ● E

ᵃ 2.开集与闭集 ᵃ ᵆ 2 ᵆ 3

内点：设G为一平面点集，Z为G的任一点，若存在 |z-z0|0)中的点都属于G,则称z0为G的内点. 开集：若G中每个点都是内点，则称G为开集。 闭集：平面上不属于G的点的全体称为G的余集， 记为CG,开集的余集称为闭集

ᵃ

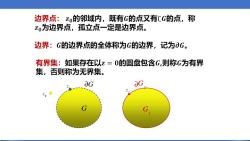
边界点：Zo的邻域内，既有G的点又有CG的点，称 z0为边界点，孤立点一定是边界点。 边界：G的边界点的全体称为G的边界，记为∂G。 有界集：如果存在以z=0的圆盘包含G,则称G为有界 集，否则称为无界集。 OG 22

ᵃ 1 ᵱ ᵃ ᵃ ᵱ ᵃ 1 ᵆ 0 ᵆ 1 ᵆ 2

3.区域 区域：设D为一平面点集，D称为区域，如果满足： (1):D是一个开集； (2):D是连通的，即D中任何两点都可用完全 属于D的折线连接起来。 即区域是连通的开集。 区域D与其边界构成闭域，记D

3.区域 即区域是连通的开集。 ᵆ 0 ᵆ 1 ᵆ 2 ᵯ ᵃ

基础练习 1:下列说法错误的是： (1)区域是开集。 (2)闭区域是闭集。 (3) 全平面即是开集又是闭集。 9 闭区域是区域

基础练习 1：下列说法错误的是： (1)区域是开集。 (2) 闭区域是闭集。 (3) 全平面即是开集又是闭集。 (4) 闭区域是区域。 √

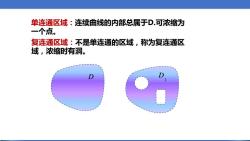
单连通区域：连续曲线的内部总属于D.可浓缩为 一个点。 复连通区域：不是单连通的区域，称为复连通区 域，浓缩时有洞

单连通区域：连续曲线的内部总属于D.可浓缩为 一个点。 复连通区域：不是单连通的区域，称为复连通区 域，浓缩时有洞。 ᵃ ᵃ 1