《复变函数与积分变换》课程教学课件（讲稿）5-1-4留数的计算

留数及其应用

留数及其应用

第四讲 留数的计算

第四讲 留数的计算

留数及其应用 1.留数定理 定理2：设函数f(z)在区域D内除有限个孤立奇点 21z2,Zn外处处解析，C是D内包围各奇点的一 条正向简单闭曲线，则 D ∮fed =2πi Res [f(z),zk] 台

留数及其应用 1.留数定理 定理2：设函数𝒇(𝒛)在区域𝑫内除有限个孤立奇点 𝒛𝟏,𝒛𝟐, . , 𝒛𝒏外处处解析，𝑪是𝑫内包围各奇点的一 条正向简单闭曲线，则 ර 𝐶𝑓 𝑧 𝑑𝑧 = 𝟐𝝅𝒊෍ 𝒌=𝟏 𝒏 𝑹𝒆𝒔 [𝒇(𝒛), 𝒛𝒌] D z1 z z 2 3 zn C1 C2 C3 Cn C

2.1函数在极点处的留数： 法则1：若zo为f(z)的简单（一阶)极点，则 Res[f(z),Zo]lim(z-zo)f(z) Z→Z0 证：若zo为f(2z)的简单（一阶）极点，则 fa=2+.a-0<k-w长 00 n=0 lim(z-zo)f(z)=c-1 Z→Z0

2.1函数在极点处的留数： 法则1：若𝒛𝟎为𝒇(𝒛)的简单（一阶）极点，则 𝑹𝒆𝒔[𝒇(𝒛),𝒛𝟎] = 𝐥𝐢𝐦 𝒛→𝒛𝟎 𝒛 − 𝒛𝟎 𝒇(𝒛) 证：若𝒛𝟎为𝒇(𝒛)的简单（一阶）极点，则 𝒇 𝒛 = 𝒄−𝟏 𝒛 − 𝒛𝟎 + ෍ 𝒏=𝟎 ∞ 𝒄𝒏 (𝒛 − z0 ) 𝒏 (𝟎 < |𝒛 − 𝒛𝟎| < 𝜹) 𝐥𝐢𝐦 𝒛→𝒛𝟎 𝒛 − 𝒛𝟎 𝒇 𝒛 = 𝒄−𝟏

举例 例1：求f(2)= 1 在各孤立奇点处的留数。 z(z-2)(z+5) 解：在z=0,z=2,z=-5,是f(z)的一阶极点，因此 ReslF(),o1=zfa)=典a-可=品 Z-0 Res[f(2),2)]=li(z-2)f(z)=lim,1 =1 737 2→2z(z+5)-14 Res,)-51=m+5f=ma=第 1=1

例1：求 𝒇 𝐳 = 𝟏 𝒛(𝒛−𝟐)(𝒛+𝟓) 在各孤立奇点处的留数。 解：在𝒛 = 𝟎, 𝒛 = 𝟐, 𝒛 = −𝟓,是𝒇(𝒛)的一阶极点，因此 𝑹𝒆𝒔[𝒇(𝒛), 𝟎] = 𝐥𝐢𝐦 𝒛→𝟎 𝒛𝒇 𝒛 = 𝑹𝒆𝒔[𝒇(𝒛), 𝟐] = 𝐥𝐢𝐦 𝒛→𝟐 𝒛 − 𝟐 𝒇 𝒛 = 𝐥𝐢𝐦 𝒛→𝟐 𝟏 𝒛(𝒛+𝟓) = 𝟏 𝟏𝟒 𝑹𝒆𝒔 𝒇 𝒛 , −𝟓 = 𝐥𝐢𝐦 𝒛→−𝟓 𝒛 + 𝟓 𝒇 𝒛 = 𝐥𝐢𝐦 𝒛→−𝟓 𝟏 𝒛−𝟐 𝒛 = 𝟏 𝟑𝟓 举例 𝐥𝐢𝐦 𝒛→𝟎 𝟏 (𝒛−𝟐)(𝒛−𝟓) = 𝟏 𝟏𝟎

2.2函数在极点处的留数 法则2：设f(a)=% Q(2) ,其中P(z),Q(z)在zo处解析， 若P(z0)≠0，zo为Q(z)的一阶零点，则zo为f(z)的 一阶极点，且 P(Z0) Reslf(z),zol=Q(zo

2.2函数在极点处的留数 法则2：设𝒇(𝒛)= 𝑷(𝒛) 𝑸(𝒛) ,其中𝑷(𝒛), 𝑸(𝒛)在𝒛𝟎处解析， 若𝑷(𝒛𝟎) ≠ 𝟎, z𝟎为𝑸(𝒛)的一阶零点，则𝒛𝟎为𝒇(𝒛)的 一阶极点，且 𝑹𝒆𝒔[𝒇(𝒛), 𝒛𝟎] = 𝑷(𝒁𝟎) 𝑸′(𝒛𝟎)

证明z为Q2)的一阶零点，故z0为高的一阶极点， “g=(@.其中n(a在0解折。且o(o+0, 由此得fa)=p2P2.a-20f= P(z) 2-Z0 z0为f(z)的一阶极点.由法则1 Reslf(z),zo=im(z-zo)F(z)=) P(Z0) 1→Z0

证明：∵ 𝒛𝟎为𝑸(𝒛)的一阶零点，故𝒛𝟎为 𝟏 𝑸(𝒛) 的一阶极点， ∴ 𝟏 𝑸(𝒛) = 𝟏 𝒛−𝒛𝟎 𝝋(𝒛)，其中𝝋 𝐳 在𝒛𝟎解析，且𝝋(𝒛𝟎)≠ 𝟎， 𝒛𝟎为𝒇(𝒛)的一阶极点. 𝒛 − 𝒛𝟎 𝒇 𝒛 = 𝑷(𝒛) 𝑸 𝒛 −𝑸(𝒛𝟎 ) 𝒛−𝒛𝟎 𝑹𝒆𝒔[𝒇(𝒛),𝒛𝟎] = = 𝑷(𝒁𝟎) 𝑸′(𝒛𝟎) 𝐥𝐢𝐦 𝒛→𝒛𝟎 𝒛 − 𝒛𝟎 𝒇(𝒛) 由法则1 由此得𝒇 𝐳 = 𝟏 𝒛−𝒛𝟎 𝝋 𝒛 𝑷(𝒛)

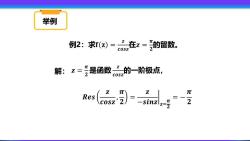
举例 例2：求（②=07在z=的留数。 解：z=是函数的一阶极点， Res π

举例 例2：求𝐟 𝐳 = 𝒛 𝒄𝒐𝒔𝒛 在𝒛 = 𝝅 𝟐 的留数。 解： 𝒛 = 𝝅 𝟐 是函数 𝒛 𝒄𝒐𝒔𝒛 的一阶极点， 𝑹𝒆𝒔 𝒛 𝒄𝒐𝒔𝒛 , 𝝅 𝟐 = ฬ 𝒛 −𝒔𝒊𝒏𝒛 𝒛= 𝝅 𝟐 = − 𝝅 𝟐

举例 例3：求f(2)=,1在z=kπ(k≠0)的留数。 zsinz 解：z=kπ(k≠0)是函数f(z)的一阶极点， Res(akm）=tdl,an=2k≠oy

举例 例3：求𝒇 𝐳 = 𝟏 𝒛𝒔𝒊𝒏𝒛在𝒛 = 𝒌𝝅(𝒌 ≠ 𝟎)的留数。 解： 𝒛 = 𝒌𝝅(𝒌 ≠ 𝟎)是函数𝒇(𝒛)的一阶极点， 𝑹𝒆𝒔 𝟏 𝒛𝒔𝒊𝒏𝒛 , 𝒌𝝅 = ቚ 𝟏 𝒔𝒊𝒏𝒛+𝒛𝒄𝒐𝒔𝒛 𝒛=𝒌𝝅 = (−𝟏) 𝒌 𝒌𝝅 (𝒌 ≠ 𝟎)

2.3函数在极点处的留数 法则3：若zo为f(z的m阶极点，则 Resif().o ((

2.3 函数在极点处的留数 法则3：若𝒛𝟎为𝒇(𝒛)的𝒎阶极点，则 𝑹𝒆𝒔[𝒇(𝒛),𝒛𝟎] = 𝟏 𝒎−𝟏 ! 𝐥𝐢𝐦 𝒛→𝒛𝟎 𝒅𝒎−𝟏 𝒅𝒛𝒎−𝟏 𝒛 − 𝒛𝟎 𝒎𝒇 𝒛 (∗)