《高等数学》课程教学课件（讲稿）8.1-2空间直角作标系

第二讲 空间直角坐标系

向量代数与空间解析几何 第二讲 空间直角坐标系

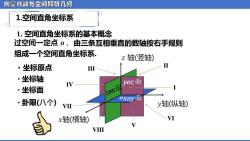
向量代数与空问解析几何 1.空间直角坐标系 1.空间直角坐标系的基本概念 过空间一定点0，由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系。 z轴（竖轴） ·坐标原点 ·坐标轴 IV 0z面 ·坐标面 ·卦限（八个） 0X02面 vI y轴（纵轴） x轴（横轴） VI VIIⅢ

向量代数与空间解析几何 Ⅶ Ⅲ Ⅱ Ⅵ Ⅷ Ⅴ Ⅳ 1.空间直角坐标系 由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系. • 坐标原点 • 坐标轴 • 坐标面 • 卦限(八个) zox面 1. 空间直角坐标系的基本概念 Ⅰ

向量代数与空间解析几何 在直角坐标系下 点M,1-1有序数组(Xy)1 向径 (称为点M的坐标) 特殊点的坐标： 原点O(0,0,0);坐标轴上的点P,Q,R; 坐标面上的点A,B,C R(0,0,2) B(0y) C(xoz) M o成.0) xPx,0,0) A(xy,0)

向量代数与空间解析几何 ᵄ ᵆ ᵆ ᵆ 在直角坐标系下 特殊点的坐标 : 有序数组(ᵆ ,ᵆ ,ᵆ ) ᵄ (ᵆ ,0,0) ᵄ (0,ᵆ ,0) ᵄ (0,0,ᵆ ) ᵃ (ᵆ ,ᵆ ,0) ᵃ (0,ᵆ ,ᵆ ) ᵃ (ᵆ ᵅ, ,ᵆ ) ᵄ

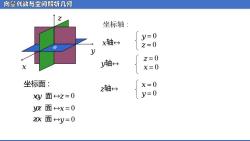
向量代数与空间解析几何 坐标轴： y=0 X轴 2=0 y轴 之=0 X=0 坐标面： ≥轴4 X=0 0y面之=0 y=0 面X=0 0x面→y=0

向量代数与空间解析几何 坐标轴 : ᵆ 轴↔ ᵆ = 0 ᵆ = 0 ᵆ = 0 ᵆ = 0 ᵆ 轴↔ ᵆ 轴↔ ᵆ = 0 ᵆ = 0 坐标面 : ᵆᵅᵆ 面↔ᵆ = 0 ᵆᵅᵆ 面 ↔ᵆ = 0 ᵆᵅᵆ 面 ↔ᵆ = 0 ᵆ ᵆ ᵆ

向量代数与空间解析几何 2.向量的坐标表示 在空间直角坐标系下，任意向量可用向径OM表示. 以，j,k,分别表示x,y,z轴上的单位向量，设点M 的坐标为M(Xyz),则 OM-ON+NM =0A+0B+OC M B =x元+yi+zk=(Xyz) 此式称为向量产的坐标分解式 N X xi,yj,zk称为向量？沿三个坐标轴方向的分向量

向量代数与空间解析几何 2. 向量的坐标表示 在空间直角坐标系下, ᵄ (ᵆ ,ᵆ ,ᵆ ), 则 沿三个坐标轴方向的分向量. = (ᵆ ,ᵆ ,ᵆ ) ᵆ ᵅ ᵆ ᵆ ᵄ ᵄ ᵃ ᵃ ᵃ 的坐标为 此式称为向量 r 的坐标分解式

向量代数与空间解析几何 2.利用坐标作向量的线性运算 设a=(ax,ay,az),b=(bx,b,bz),为实数，则 d±b=(ax±bx,ay±by,az±bz), λa=(2ax,ay,1az), 平行向量对应坐标成比例： 当a≠可时， b b‖a台b=λa bx by bz ←→ ax ay az

向量代数与空间解析几何 2. 利用坐标作向量的线性运算 平行向量对应坐标成比例: ᵈ ᵉ = ᵴ ᵈ ᵉ ᵈ ᵉ = ᵴ ᵈ ᵉ ᵈ ᵉ = ᵴ ᵈ ᵉ

向量代数与空间解析几何 举例 例1.求解以向量为未知元的线性方程组. { 5元-3列=① 3元-2列=6 ② 其中=(2,1,2)，b=(-1,1,-2), 解：2×①一3×②，得 x=2d-3b=(7,-1,10) 代入②得 =23-6=(11,-2,16

向量代数与空间解析几何 举例 例1.求解以向量为未知元的线性方程组. ① ② 解: 2×① －3×② ,得 = (7, − 1,10) 代入②得 = (11, − 2,16)

向量代数与空间解析几何 举例 例2.已知两点A=(x1,y1,z1), B=(x2,y2,z2)及实数1≠-1， 在直线AB上求一点M,使AM=λMB 解：设M的坐标为(x,y,z),如图所示 M AM=λMB B AM-OM-OA 0 MB-0B-OM A 0M-0A=λ(0B-0 得 0M=1(0A+0B) B 1+入 1 M 即(Xyr）= 1+元(x1+x2y1+y2,乙1+1z2)

向量代数与空间解析几何 举例 ᵃ ᵃ ᵄ ᵅ ᵄ ᵃ 得 ᵃ 即(ᵆ ,ᵆ ,ᵆ ) =

向量代数与空间解析几何 说明：由 1+71+x2h+2,a+z) (2）= 得定比分点公式： t x1+几 1+λ 2, y= 1+y, a= z1+九z2 1+λ 1+入 当λ=1时，点M为AB的中点，于是得 中点公式： X三 ，y=4,2=+2 x1+x2 2 2 2

向量代数与空间解析几何 说明: 由 (ᵆ ,ᵆ ,ᵆ ) = 得定比分点公式: 中点公式:

向量代数与空间解析几何 3.向量的模、方向角、投影 1.向量的模与两点间的距离公式 R 设分=(x,y,z),作0M=元，则有 M 子=0M=0P+0Q+0R Q 由勾股定理得 P OM=IOFR2+10012+0Ry+z 对两点A(x1,y1,乙1)与B(x2,y2,Z2),因 B AB=0B-0A=(X2-y2-y122-2) 得两点间的距离公式： A |AB=AB=V(x2-x1)2+(02-y1)2+(22-Z1)2

向量代数与空间解析几何 3. 向量的模、方向角、投影 1. 向量的模与两点间的距离公式 则有 ᵆ ᵅ ᵆ ᵆ ᵄ ᵄ ᵄ ᵄ 由勾股定理得 ᵄ 因 ᵃ ᵃ 得两点间的距离公式: = (ᵆ 2 − ᵆ 1 , ᵆ 2 − ᵆ 1 , ᵆ 2 − ᵆ 1 )