《高等数学》课程教学课件（讲稿）10-1-6三重积分的计算

第十章 重积分

重积分 第十章 重 积 分

第六讲 三重积分的计算

重积分 第六讲 三重积分的计算

重积分 1柱坐标计算三重积分 设M(x,y,z)∈R3,将x,y用极坐标p,代替，则（p,0,z) 就称为点M的柱坐标.直角坐标与柱面坐标的关系： x=pcos0 0≤p<+∞ y=psin0 0≤0≤2π -0∞<Z<十∞ z=Z M(,y,z) 坐标面分别为 p=常数 圆柱面 +V 0=常数 半平面 (x,y,0) z=常数 平面

重积分 1.柱坐标计算三重积分 o 𝑥 𝑦 𝑧 设𝑀(𝑥, 𝑦, 𝑧) ∈ R 3 , 将𝑥, 𝑦用极坐标𝜌, 𝜃代替, 则（𝜌, 𝜃, 𝑧) 就称为点M 的柱坐标. 0 ≤ 𝜌 < +∞ 0 ≤ 𝜃 ≤ 2𝜋 −∞ < 𝑧 < +∞ 𝑦 = 𝜌 sin 𝜃 𝑧 = 𝑧 𝑥 = 𝜌 cos 𝜃 直角坐标与柱面坐标的关系: 𝜌 = 常数 坐标面分别为 圆柱面 𝜃 = 常数 半平面 𝑧 = 常数 平面 𝑜 𝜃 z 𝑀(𝑥, 𝑦, 𝑧) 𝜌 (𝑥, 𝑦, 0)

重积分 如图所示，在柱面坐标系中体积元素为 dv=pdpdedz pd0 因此 ∬nfx,y,2)du =jnF(p,日，z)pdpd8dz 其中F(p,0,Z)=f(pcos0,psin8,z) 适用范围： 1)积分域表面用柱面坐标表示时方程简单； 2)被积函数用柱面坐标表示时变量互相分离

重积分 如图所示, 在柱面坐标系中体积元素为 z 𝜌 d 𝑧 d 𝜌 𝜌 d 𝜃 𝜃 d 𝑣 = 𝜌 d 𝜌 d 𝜃 d 𝑧 因此 ʃʃʃΩ 𝑓(𝑥, 𝑦, 𝑧) d 𝑣 = ʃʃʃΩ𝐹(𝜌, 𝜃, 𝑧)𝜌 d 𝜌 d 𝜃 d 𝑧 其中 𝐹(𝜌, 𝜃, 𝑧) = 𝑓(𝜌 cos 𝜃 , 𝜌 sin 𝜃 , 𝑧) 适用范围: 1) 积分域表面用柱面坐标表示时方程简单 ; 2) 被积函数用柱面坐标表示时变量互相分离. 𝑥 𝑦 𝑧 o  d 𝜌 𝑑𝜃

重积分 例1.计算三重积分z√x2+y2 dxdydz其中2为由 柱面x2+y2=2x及平面z=0,z=a(a>0),y=0所围 成半圆柱体 0≤p≤2cos 解：在柱面坐标系下2： Z 0≤0≤2 原式=nzp2dpd0dz 0≤z≤a 0人 |2 2c0s0 2 p=2 cos0 zdz de p2dp 4a2 π/ 2 cos3 0de 8 9=ga3 dv=pdpdθdz

重积分 例1. 计算三重积分 其中为由 𝑥 2 + 𝑦 2 = 2𝑥 𝑧 = 0, 𝑧 = 𝑎 (𝑎 > 0), 𝑦 = 0 所围 解: 在柱面坐标系下 න 0 2 cos 𝜃 𝜌 2 d 𝜌 = 4𝑎 2 3 න 0 ൗ 𝜋 2 cos3 𝜃 d 𝜃 Ω: 0 ≤ 𝜌 ≤ 2 cos 𝜃 0 ≤ 𝜃 ≤ 𝜋 2 0 ≤ 𝑧 ≤ 𝑎 及平面 2 𝑎 𝑥 𝑦 𝑧 𝑜 d 𝑣 = 𝜌 d 𝜌 d 𝜃 d 𝑧 න 0 ൗ 𝜋 2 = න d 𝜃 0 𝑎 𝑧 d 𝑧 原式 = ʃʃʃΩ z𝜌 2 d 𝜌 𝑑𝜃𝑑𝑧 = 8 9 𝑎 3 柱面 𝜌 = 2 cos 𝜃 成半圆柱体. ʃʃʃΩ 𝑧 𝑥 2 + 𝑦 2 d 𝑥 d 𝑦 d 𝑧

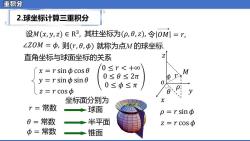
重积分 2.球坐标计算三重积分 设M(x,y,z)∈R3,其柱坐标为(p,0,z),令1OM1=r, LZ0M=中，则(r,0,中)就称为点M的球坐标 直角坐标与球面坐标的关系 Z x=rsinΦcos0 0≤r<+∞ M y=rsinΦsin0 0≤0≤2π 0≤φ≤π 0 z=rC0S中 坐标面分别为 r=常数 球面 p=rSinΦ 0=常数 半平面 z=rCoSΦ 中=常数 锥面

重积分 2.球坐标计算三重积分 设𝑀(𝑥, 𝑦, 𝑧) ∈ R 3 , 其柱坐标为(𝜌, 𝜃, 𝑧), 就称为点M 的球坐标. 直角坐标与球面坐标的关系 ∠𝑍𝑂𝑀 = 𝜙, 𝜌 𝜃 𝑀 𝑜 𝑥 𝑦 𝑧 z 𝜙 𝑟 则(𝑟, 𝜃,𝜙) 0 ≤ 𝑟 < +∞ 0 ≤ 𝜃 ≤ 2𝜋 0 ≤ 𝜙 ≤ 𝜋 𝑥 = 𝑟 sin𝜙 cos 𝜃 𝑦 = 𝑟 sin𝜙 sin 𝜃 𝑧 = 𝑟 cos𝜙 坐标面分别为 𝑟 = 常数 球面 𝜃 = 常数 半平面 𝜙 = 常数 锥面 令 𝑂𝑀 = 𝑟, 𝑀(𝑟, 𝜃, 𝜙) 𝜌 = 𝑟 sin𝜙 𝑧 = 𝑟 cos𝜙

重积分 如图所示，在球面坐标系中体积元素为 dv=r2sinΦdrdΦd0 因此有 ∬nfxy,2）)dxdydz d功 F(r,8,Φ)r2sin中drd中d6 dθ 其中F(r,0,中)=f(rsin中cos0,rsin中sin0,r cos p) 适用范围： 1)积分域表面用球面坐标表示时方程简单； 2)被积函数用球面坐标表示时变量互相分离

重积分 𝑥 𝑦 𝑧 o 如图所示, 在球面坐标系中体积元素为 d𝜙 𝑑𝜃 𝜙 𝑟 d 𝑟 d 𝑣 = 𝑟 2 sin𝜙 d 𝑟 d𝜙 d 𝜃 因此有 ʃʃʃΩ 𝑓(𝑥, 𝑦, 𝑧) d𝑥𝑑𝑦 𝑑𝑧 其中 𝐹(𝑟, 𝜃,𝜙) = 𝑓(𝑟 sin𝜙 cos 𝜃 , 𝑟 sin𝜙 sin 𝜃 , 𝑟 cos𝜙) 适用范围: 1) 积分域表面用球面坐标表示时方程简单; 2) 被积函数用球面坐标表示时变量互相分离.  d 𝜃 𝐹(𝑟, 𝜃,𝜙)𝑟 2 ʃʃʃ sin𝜙 d 𝑟 d𝜙 d 𝜃 Ω

重积分 例2.计算三重积分 ∬n(x2+y2+z3)dxdy dz.其中2 为锥体z=Vx2+y2 与球面x2+y2+z2=R2所围立体 解：在球面坐标系下 0≤r≤R π 2:了0≤中≤ 0<0≤3u j∬(x2+y2+z")axdy dz =d0snd中rr dv=r2sinφdrdφd0 =亏πR5(2-V2)

重积分 例2. 计算三重积分 为锥体𝑧 = 𝑥 2 + 𝑦 2 𝑥 2 + 𝑦 2 + 𝑧 2 = 𝑅 2 解: 在球面坐标系下 Ω: ∴ ʃʃʃΩ (𝑥 2 + 𝑦 2 + 𝑧 2 ) d𝑥𝑑𝑦 𝑑𝑧 所围立体. 0 ≤ 𝜙 ≤ 𝜋 4 0 ≤ 𝑟 ≤ 𝑅 0 ≤ 𝜃 ≤ 2𝜋 其中 与球面 d 𝑣 = 𝑟 2 sin𝜙 d 𝑟 d𝜙 d 𝜃 න 0 𝑅 𝑟 4 d 𝑟 = 1 5 𝜋𝑅 5 (2 − 2) න 0 ൗ 𝜋 4 = න sin𝜙 d𝜙 0 2𝜋 d 𝜃 𝑥 𝑦 𝑧 o 4  r = R ʃʃʃΩ (𝑥 2 + 𝑦 2 + 𝑧 2 ) d𝑥𝑑𝑦 𝑑𝑧

重积分 课堂小结 1.三重积分在柱面坐标系的计算 0≤p<+∞ y=psine 0≤0≤2π Z=Z -0∞<z<+00 2.三重积分在球面坐标系的计算 x=rsinΦcos0 /0≤r<+∞ y=rsino sine 0≤0≤2π z=rC0S中 N0≤φ≤π

重积分 课 堂 小 结 1. 三重积分在柱面坐标系的计算 2. 三重积分在球面坐标系的计算 0 ≤ 𝜌 < +∞ 0 ≤ 𝜃 ≤ 2𝜋 −∞ < 𝑧 < +∞ 𝑦 = 𝜌 sin 𝜃 𝑧 = 𝑧 𝑥 = 𝜌 cos 𝜃 𝑥 = 𝑟 sin𝜙 cos 𝜃 𝑦 = 𝑟 sin𝜙 sin 𝜃 𝑧 = 𝑟 cos𝜙 0 ≤ 𝑟 < +∞ 0 ≤ 𝜃 ≤ 2𝜋 0 ≤ 𝜙 ≤ 𝜋

工作人员 总策划：卢自娟 主讲人：卢自娟 脚本策划：卢自娟 李达玲 里提甫·玉素甫 黄光迪张晗 冀彦

重积分 工 作 人 员 总策划：卢自娟 主讲人：卢自娟 脚本策划：卢自娟 李达玲 里提甫·玉素甫 黄光迪 张 晗 冀 彦