《高等数学》课程教学课件（讲稿）5-2定积分的性质

第二讲 定积分的性质

定积分及其应用 第二讲 定积分的性质

定积分及其应用 定积分的性质 性质1∫f(x)±g(x]dx=f(x)dx±∫g(x)dx 即两个函数和（差)的定积分等于它们定积分的和（差）· n 证：f[fox)±g(x]dx=g∑f)±95]△x 11 =∑r±∑9a=f)t±公g i=1 注 1、 本课程所有性质中研究的函数均为可积函数。 意 2、性质1可以推广到有限多个函数作和的情况

定积分及其应用 性质１ 即两个函数和（差）的定积分等于它们定积分的和（差）． 证： 注 意 1、本课程所有性质中研究的函数均为可积函数。 2、性质1可以推广到有限多个函数作和的情况。 一. 定积分的性质

定积分及其应用 性质2积分数乘性质 kf(x)dx =kf(x)dx (k为常数) 即被积函数的常数因子可以提到积分号外. ■性质4[积分线性性质] 21dx口的dc口b加a y=1

定积分及其应用 性质２ [积分数乘性质 ] 即被积函数的常数因子可以提到积分号外． 性质4 [积分线性性质] ᵄ ᵄ ᵄ ᵆ ᵆ ᵆ = 1

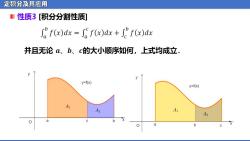
定积分及其应用 ■性质3[积分分割性质] f(x)dx f(x)dx+f(x)dx 并且无论a、b、c的大小顺序如何，上式均成立. y=f(x) y=f(x) A A2 A A2 a b

定积分及其应用 性质3 [积分分割性质]

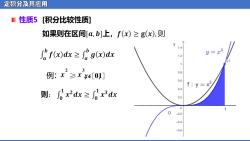
定积分及其应用 ■性质5[积分比较性质] 如果则在区间[a,b]上，f(x)≥g(x),则 2fx)dx≥hgx)dx 12 y=x3 1 例：x≥xxe[0] 08 06 f:y=x2 0.4 则：0x2dx≥0x3dx 02 0.2 -0.4 -0.6

定积分及其应用 性质5 [积分比较性质] 例：ᵉ ᵽ ≥ ᵉ ᵽ ,ᵉ ᵵ [ᵼ ,ᵼ ]

定积分及其应用 ■性质6[积分估值性质] 设M及m分别是函数f(x)在区间[a,b]上的最大值和最小值，则： m(b-a)≤∫f(x)dx≤M(b-a). 证： .'m≤f(x)≤M mdx≤2fx)dx≤Mdx 则m(b-a)≤J也f(x)dx≤M(b-a) 注 意 此性质可用于估计积分值的大致范围

定积分及其应用 性质6 [积分估值性质] 证： 则 此性质可用于估计积分值的大致范围。 ∵ ᵈ ≤ ᵈ(ᵉ ) ≤ ᵇ 注 意 估值 估值

定积分及其应用 b m(b-a)≤f(x)dx≤Mb-a 个y y=f(x) M m 估值

定积分及其应用 O x y y=f (x) a b M m 估值

定积分及其应用 ■性质7[积分中值定理] 如果函数f(x)在闭区间[a,b]上连续，则在 积分区间[a,b]上至少存在一个点彩，使得 估值 2f(x)dx=f(5)b-a)(a≤5≤b). 证：：m(b-a)≤J2f(x)dx≤M(b-a) m≤ f()dx ≤M b-a 闭区间上连续函数平均值公式 由闭区间上连续函数的介值足 f区间[a,b]上 至少存在一个点彩，使得 f()=0 f()dx b-a 即f(x)dx=f(5)(b-a）(a≤5≤b)

定积分及其应用 性质7 [积分中值定理] 证： 即 闭区间上连续函数平均值公式 估值 估值

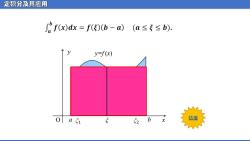
定积分及其应用 f(x)dx=f5(b-a)(a≤专≤b). y=f(x) 0a51 b 估值 S2

定积分及其应用 O x y y=f (x) a ξ b 估值

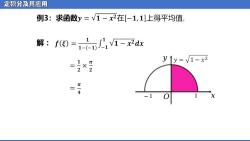
定积分及其应用 例3：求函数y=V1-x2在[-1,1]上得平均值. 解：f)=1-1-x ↑y=V1-x2 = π π一4 X

定积分及其应用 解： ᵆ ᵆ − 1 ᵄ 1