《高等数学》课程教学课件（讲稿）6-2定积分的性质

第二讲 定积分的性质

第二讲 定积分的性质

定积分及其应用 一.定积分的性质 性质1f(x)±g(x]dx=∫f(x)dx±g(x)dx 即两个函数和（差）的定积分等于它们定积分的和（差） 证：Lf()士g(x]ax=∑f5)±gax =r0主sa=7 CirLPny 注 1、 本课程所有性质中研究的函数均为可积函数。 意 2、性质1可以推广到有限多个函数作和的情况

性质１ 即两个函数和（差）的定积分等于它们定积分的和（差）． 证： 注 意 1、本课程所有性质中研究的函数均为可积函数。 2、性质1可以推广到有限多个函数作和的情况。 一. 定积分的性质 ��׬ 𝑏 ��׬ = �𝑑� �� �� ± �� �� 𝑏 ��׬ ± �𝑑� �� �� 𝑏 𝑔 𝑥 𝑑𝑥 ��׬ 𝑏 𝑓 𝑥 ± 𝑔 𝑥 𝑑𝑥 = 𝑙𝑖𝑚 𝜆→0෍ 𝑖=1 𝑛 [𝑓(𝜉𝑖) ± 𝑔(𝜉𝑖)]∆𝑥𝑖 = 𝑙𝑖𝑚 𝜆→0෍ 𝑖=1 𝑛 𝑓(𝜉𝑖)∆𝑥𝑖 ± 𝑙𝑖𝑚 𝜆→0෍ 𝑖=1 𝑛 ��׬ = �𝑥�∆(�𝜉�)�� 𝑏 ��׬ ± �𝑑� �� �� 𝑏 𝑔 𝑥 𝑑𝑥

定积分及其应用 ■性质2[积分数乘性质] 由kf(x)dx=kj2f(x)dx (k为常数) 即被积函数的常数因子可以提到积分号外. ■性质4[积分线性性质] =1 ∫1c=∫dc=b-. 6

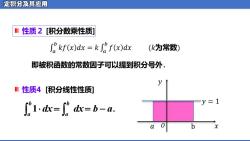
性质２ [积分数乘性质] 即被积函数的常数因子可以提到积分号外． 性质4 [积分线性性质] dx b a   1 dx b a = = b − a. ��׬ 𝑏 ��׬ �� = �𝑑� �� �𝑘� 𝑏 𝑓 𝑥 𝑑𝑥 (𝑘为常数) 𝑎 𝑂 b 𝑥 𝑦 𝑦 = 1

定积分及其应用 ■性质3[积分分割性质] f(x)dx Jf(x)dx+f(x)dx 并且无论a、b、c的大小顺序如何，上式均成立 y=f(x) y=f(x) A A2 A A2 a b

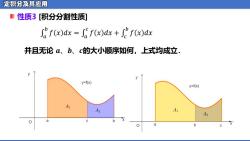
并且无论 𝒂、𝒃、𝒄的大小顺序如何，上式均成立． 性质3 [积分分割性质] ��׬ 𝑏 ��׬ = �𝑑� �� �� 𝑐 ��׬ + �𝑑� �� �� 𝑏 𝑓 𝑥 𝑑𝑥

定积分及其应用 ■性质5[积分比较性质] 如果则在区间[a,b]上，f(x)≥g(x),则 af(x)drx≥ag(x)dx 12 y=x3 1 例：x2≥x3,xe[0,1] 08 06 f:y=x2 0.4 则：x2dx≥6xdx 02 02 -0.4 -0.6

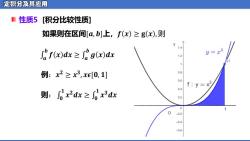
性质5 [积分比较性质] 如果则在区间[𝒂, 𝒃]上，𝒇 𝒙 ≥ 𝐠 𝒙 , 则 例：𝒙 𝟐 ≥ 𝒙 𝟑 , 𝒙𝝐[𝟎, 𝟏] ��׬ :则 𝟏 𝒙 ��׬ ≤ �𝒅𝟐� 𝟏 𝒙 𝟑𝒅𝒙 ��׬ 𝒃 ��׬ ≤ �𝒅� �� �� 𝒃 𝒈 𝒙 𝒅𝒙

定积分及其应用 ■性质6[积分估值性质] 设M及m分别是函数f(x)在区间[a,b]上的最大值和最小值，则： m(b-a)≤∫2f(x)dx≤M(b-a. 证： 'm≤f(x)≤M mdx≤Jfx)dx≤Mdx 则m(b-a)≤f(x)dx≤M(b-a) 注 此性质可用于估计积分值的大致范围。 意

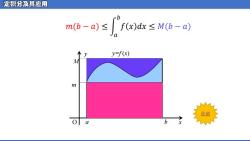
性质6 [积分估值性质] 证： 则 此性质可用于估计积分值的大致范围。 设𝑴及𝒎分别是函数𝒇(𝒙)在区间[𝒂, 𝒃]上的最大值和最小值，则： ��׬ ≥ �� − �� �� 𝒃 𝒇 𝒙 𝒅𝒙 ≤ 𝑴 𝒃 − 𝒂 . ��׬ ≥ (�� − ��)�� 𝒃 𝒇 𝒙 𝒅𝒙 ≤ 𝑴(𝒃 − 𝒂) ∵ 𝒎 ≤ 𝒇(𝒙) ≤ 𝑴 ��׬ ∴ 𝒃 ��׬ ≥ �𝒅� �� 𝒃 ��׬ ≥ �𝒅� (��)�� 𝒃 𝑴 𝒅𝒙 注 意 估值 估值

定积分及其应用 6 mb-a)≤f)dx≤Mb-a) 个y y=f(x) M m 0

O x y y=f (x) a b M 𝑚(𝑏 − 𝑎) ≤ න 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 ≤ 𝑀(𝑏 − 𝑎) m 估值

定积分及其应用 ■性质7[积分中值定理] 如果函数f(x)在闭区间[a,b]上连续，则在 积分区间[α，b]上至少存在一个点ξ，使得 估值 2fx)dx=f(5)(b-a)(a≤5≤b). 证：m(b-a)≤∫f(x)dx≤M(b-a) f(x)dx .m≤ ≤M b-a 闭区间上连续函数平均值公式 由闭区间上连续函数的介值足] f区间[a,b]上 f(x)dx 至少存在一个点影，使得f(5)= b-a 即∫f(x)dx=f(ξ)(b-a)(a≤ξ≤b)

性质7 [积分中值定理] 证： 由闭区间上连续函数的介值定理知：在区间 [𝒂, 𝒃]上 即 闭区间上连续函数平均值公式 ��׬ ≥ (�� − ��)�� ∵ 𝑏 𝑓 𝑥 𝑑𝑥 ≤ 𝑀(𝑏 − 𝑎) 如果函数𝒇(𝒙)在闭区间[𝒂, 𝒃]上连续，则在 积分区间[𝒂, 𝒃]上至少存在一个点𝝃，使得 ��׬ 𝑏 𝑓 𝑥 𝑑𝑥 = 𝑓 𝜉 𝑏 − 𝑎 (𝑎 ≤ 𝜉 ≤ 𝑏). 至少存在一个点𝝃，使得 ��׬ 𝑏 𝑓 𝑥 𝑑𝑥 = 𝑓 𝜉 𝑏 − 𝑎 (𝑎 ≤ 𝜉 ≤ 𝑏). 𝑓(𝜉)= ��׬ 𝑏 𝑓 𝑥 𝑑𝑥 𝑏−𝑎 . ∴ 𝑚 ≤ ��׬ 𝑏 𝑓 𝑥 𝑑𝑥 𝑏 − 𝑎 ≤ 𝑀 估值 估值

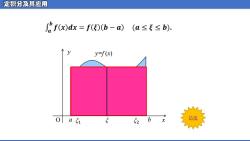
定积分及其应用 f(x)dx=f(5)(b-a)(a≤专≤b). y=f(x) 0a51 52 b 估值

O x y y=f (x) a ξ b ��׬ 𝒃 𝒇 𝒙 𝒅𝒙 = 𝒇 𝝃 𝒃 − 𝒂 (𝒂 ≤ 𝝃 ≤ 𝒃). ξ1 ξ2 估值

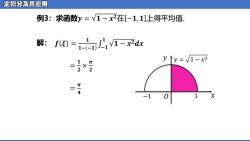
定积分及其应用 例3：求函数y=V1-x2在[-1,1]上得平均值. 解：f③=1-xdx yly=v1-x2 = π一4

例3：求函数𝒚 = 𝟏 − 𝒙 𝟐在 −𝟏, 𝟏 上得平均值. 𝒇 𝝃 = 𝟏 𝟏− −𝟏 ��−׬ 𝟏 𝟏 − 𝒙 解： 𝟐𝒅𝒙 = 𝝅 𝟒 = 𝟏 𝟐 × 𝝅 𝟐 𝑥 𝑦 −1 𝑂 1 𝑦 = 1 − 𝑥 2