《高等数学》课程教学课件（讲稿）4-1微分中值定理

第一讲 微分中值定理

第一讲 微分中值定理

中值定理与导数应用 一.微分中值定理 利用导数来研究函数在区间上的特性 1.罗尔中值定理 2.拉格朗日中值定理 拉格朗日中值定理又称拉氏定理，是微分学中的基本定 理之一，它反映了可导函数在闭区间上的整体的平均变 化率与区间内某点的局部变化率的关系。拉格朗日中值 定理是罗尔中值定理的推广，同时也是柯西中值定理的 特殊情形，是泰勒公式的弱形式（一阶展开）

拉格朗日中值定理又称拉氏定理，是微分学中的基本定 理之一，它反映了可导函数在闭区间上的整体的平均变 化率与区间内某点的局部变化率的关系。拉格朗日中值 定理是罗尔中值定理的推广，同时也是柯西中值定理的 特殊情形，是泰勒公式的弱形式（一阶展开）。 利用导数来研究函数在区间上的特性 一.微分中值定理 1.罗尔中值定理 2.拉格朗日中值定理

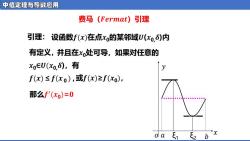
中值定理与导致应用 费马(Fermat)i 引理 引理：设函数f(x)在点xo的某邻域U(xo.)内 有定义，并且在x处可导，如果对任意的 xo∈U(xo,6),有 f(x)≤f(xo),或f(x)≥f(xo), 那么f'(xo)=0 oa1 E2 bx

费马（𝑭𝒆𝒓𝒎𝒂𝒕）引理 引理： 设函数𝒇(𝒙)在点𝒙0的某邻域𝑼(𝒙0,𝜹)内 𝒇(𝒙)≤𝒇(𝒙 0 )， 𝒙0∈𝑼(𝒙0,𝜹)，有 那么𝒇 ′ (𝒙0 )=𝟎 有定义， 𝑦 𝑥 𝑜 ξ1 ξ2 𝑎 𝑏 并且在𝒙0处可导，如果对任意的 或𝒇(𝒙)≥𝒇(𝒙0 )

中值定理与导数应用 罗尔(Rollr)中值定理 定理1： 如果函数f(x): 在[a,b]上连续； 在(a,b)内可导； f(a)=f(b), 那么在(a,b)内至少 有一点(a<<b), 使得f'()=0. 0aξ1&2bx

定理1： 罗尔(𝑹𝒐𝒍𝒍𝒓)中值定理 如果函数𝒇(𝒙): 𝒇(𝒂) = 𝒇(𝒃)， 在(𝒂, 𝒃)内可导； 那么在(𝒂, 𝒃)内至少 有一点𝝃(𝒂 < 𝝃 < 𝒃), 在[𝒂, 𝒃]上连续； 使得𝒇 ′ (𝝃) =0. 𝑦 𝑥 o ξ1 ξ2 𝑎 𝑏

中值定理与导数应用 例1：验证下列函数是否满足罗尔中值定理。 (1)y=x2 x∈[-2,2] 证明：显然y=x2在[-2,2]上连续，在(-2,2)上可导， 且f(-2)=f(2)=4; 满足 故：f()=2ξ=0，即ξ=0. (2)y=Ix|x∈[-1,1] 不满足 因为在(-1,1)上不可导

例1：验证下列函数是否满足罗尔中值定理。 (𝟏) 𝒚 = 𝒙 2 𝒙∈[−𝟐, 𝟐] (𝟐) 𝒚 = |𝒙| 𝒙 ∈ [−𝟏, 𝟏] 证明：显然𝒚 = 𝒙 2在[−𝟐, 𝟐]上连续，在(−𝟐, 𝟐)上可导， 故： 𝒇 ´(𝝃) = 𝟐𝝃 = 𝟎,即𝝃 = 𝟎. 满足 因为在(−𝟏, 𝟏)上不可导。 不满足 且𝒇(−𝟐) = 𝒇(𝟐) = 𝟒;

中值定理与导数应用 拉格朗日(Lagrange)中值定理 定理2：如果函数f(x): 在[a,b]上连续； 在(a,b)内可导： f(b)-f(a) 那么在(a,b)内至少 有一点(a<<b), 使得f'(3)=fb)-f@ b-a oaξ1 2b七 f(b)-f(a)=f'()(b-a)·

定理2： 拉格朗日（𝑳𝒂𝒈𝒓𝒂𝒏𝒈𝒆）中值定理 如果函数𝒇(𝒙): 在(𝒂, 𝒃)内可导； 那么在(𝒂, 𝒃)内至少 有一点𝝃(𝒂 < 𝝃 < 𝒃), 在[𝒂, 𝒃]上连续； 𝒚 o 𝒙 ξ1 ξ2 𝒂 𝒃 𝒇(𝒃) − 𝒇(𝒂) 𝒇(𝒃) − 𝒇(𝒂) = 𝒇´(𝝃)(𝒃 − 𝒂) . 使得𝒇 ′ 𝝃 = 𝒇 𝒃 −𝒇(𝒂) 𝒃−𝒂

中值定理与导数应用 例2：求下列函数满足拉格朗日中值定理的值。 (1)y=x3x∈[-1,2] 解：显然y=x3在[-1,2]上连续， 在(-1,2)上可导， 使得f'(闭=32==3 故：ξ=1，=-1（舍去）·

例2：求下列函数满足拉格朗日中值定理的𝝃值。 (1) 𝒚 = 𝒙 3 𝒙 ∈ [−𝟏, 𝟐] 解： 显然𝒚 = 𝒙 3在[−𝟏, 𝟐]上连续， 在(−𝟏, 𝟐)上可导， 故：𝝃 = 𝟏, 𝝃 = −𝟏（舍去）. 使得𝒇 ′ 𝝃 = 3𝝃 𝟐 = 𝟖+𝟏 𝟐+𝟏 = 𝟑

中值定理与导致应用 练习：求下列函数满足拉格朗日中值定理的值 (1)y=x2,x∈[0,1] 2ξ=1 5=月 (2)验证下列函数是否满足罗尔中值定理。 y=lnxx∈[1，e] 不满足

练习： 求下列函数满足拉格朗日中值定理的𝝃值。 (1)𝒚 = 𝒙 𝟐 , 𝒙 ∈ [𝟎, 𝟏] (2)验证下列函数是否满足罗尔中值定理。 𝒚 = 𝒍𝒏𝒙 𝒙 ∈ [𝟏, 𝒆] 不满足 2𝜉=1 𝜉= 1 2

中值定理与导致应用 推论1：如果函数f(x)在(a,b)内可导 且f'(x)=0,则在(a,b)内f(x)是一常数. f(x1)-f(x2)=f'()(x1-x2)=0(x1-x2)=0 (任取x1x2属于(a,b) 推论2：如果函数f(x),g(x)在(a,b)内可导，且f'(x)=g'(x), 则在(a,b)内f(x)=g(x)+C(C是一常数). 设F(x)=f(x)-g(x), 因为f'(x)-g'(x)=0 所以f(x)-g(x)=C

推论1：如果函数𝒇(𝒙)在(𝒂, 𝒃)内可导， 且𝒇 ´(𝒙) = 𝟎，则在(𝒂, 𝒃)内𝒇(𝒙)是一常数. 推论2： 则在(𝒂, 𝒃)内𝒇(𝒙) = 𝒈(𝒙) + 𝑪(𝑪是一常数). 如果函数𝒇(𝒙)，𝒈(𝒙)在(𝒂, 𝒃)内可导，且𝒇 ′ 𝒙 = 𝒈′(𝒙)， 𝒇(𝒙𝟏 ) − 𝒇(𝒙𝟐 ) = 𝒇´(𝝃)(𝒙𝟏 − 𝒙𝟐 ) = 𝟎(𝒙𝟏 − 𝒙𝟐 ) = 𝟎 (任取𝒙𝟏 , 𝒙𝟐属于(𝒂, 𝒃) 设𝑭(𝒙) = 𝒇(𝒙) − 𝒈(𝒙), 因为𝒇´(𝒙) − 𝒈´(𝒙) = 𝟎 所以𝒇(𝒙) − 𝒈(𝒙) = 𝑪

中值定理与导数应用 课堂小结 罗尔中值定理 中值定理 拉格日朗日中 值定理 拉格日朗日中值定理的推论

课 堂 小 结 中值定理 罗尔中值定理 拉格日朗日中 值定理 拉格日朗日中 值定理的推论