《高等数学》课程教学课件（讲稿）4-2函数的单调性

第二讲 函数的单调性

第二讲 函数的单调性

中值定理与导数应用 引例： 设质点作直线运动，其运动规律为： 1 s=44-4t3+102(t>0) (1)何时速度为零？ (2)何时作前进运动？ (3)何时作后退运动？

引例： 设质点作直线运动，其运动规律为： 𝒔 = 𝟏 𝟒 𝒕 𝟒 − 𝟒𝒕𝟑 + 𝟏𝟎𝒕𝟐(𝒕 > 𝟎) (1)何时速度为零？ (2)何时作前进运动？ (3)何时作后退运动？

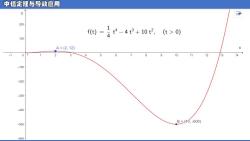
中值定理与导激应用 y 海 200 -4+10民，(t>0 ft)=4 100 A=(2,12) X o f 1 2 3 10 11 2 13 14→ -100 -200 -300 400 B=(40,-500) 500 600

中值定理与导数应用 y=f(x)xE∈(a,b) 单调递增 单调递减 即f'(x)>0. 即f'(x)<0

即𝑓´(𝑥) > 0. 𝑦 = 𝑓(𝑥) 𝑥 ∈ (𝑎, 𝑏) 即𝑓´(𝑥) < 0. 单调递增 单调递减

中值定理与导敛应用 1.函数的单调性 定理1：如果函数f(x): 在[a,b1上连续； 在(a,b)内可导： (1)如果在(a,b)内f'(x)≥0，则f(x)在[a,b]上单调增加。 (2)如果在(a,b)内f'(x)≤0，则f(x)在[ab]上单调减少。 说明：区间可[a,b],(a,b),(a,b],[a,b) 只有有限个点处导数为零

定理1： 如果函数𝒇(𝒙): 在[𝒂, 𝒃]上连续； 在(𝒂, 𝒃)内可导； (1)如果在(𝒂, 𝒃)内𝒇´(𝒙) ≥ 𝟎, 则𝒇(𝒙)在[𝒂, 𝒃]上单调增加。 (2)如果在(𝒂, 𝒃)内𝒇´(𝒙) ≤ 𝟎, 则 𝒇(𝒙) 在 [𝒂, 𝒃] 上单调减少。 说明：区间可[𝒂, 𝒃], (𝒂, 𝒃)，(𝒂, 𝒃],[𝒂, 𝒃) 1.函数的单调性 只有有限个点处导数为零

中值定理与导数应用 例1：判断下列函数的单调性。 (1)y=Inx 解：xE0+m,y-是cx>0) 故：y=lnx在(0，+o)上单调递增。 ⊕

例1： 判断下列函数的单调性。 (1) 𝒚 = 𝒍𝒏𝒙 解： 𝒙 ∈ (𝟎, +∞)， 故： (𝒙 > 𝟎) 𝒚 = 𝒍𝒏𝒙在(𝟎, +∞)上单调递增。 𝒚 ′ = 𝟏 𝒙

中值定理与导数应用 (2)y=ex-x-1 解：x∈(-o,+o), y'=ex-1,令y'=0,x=0, X (-∞，0) 0 (0,+∞) y 0 + y y 故：y=ex-x-1在(-∞，0]上单减， 在(0，+0)上单增

(2) 𝒚 = 𝒆 𝒙 − 𝒙 − 𝟏 解： 𝒙 ∈ (−∞, +∞)， 𝒚 ´ = 𝒆 𝒙 − 𝟏,令𝒚′ = 𝟎, 𝒙 = 𝟎, 𝑥 𝑦 ´ 𝑦 故： 𝒚 = 𝒆 𝒙 − 𝒙 − 𝟏在(−∞, 𝟎]上单减， 在 (𝟎, +∞) 上单增。 (−∞, 0) 0 (0, +∞) − + 0 ↘ ↗

中值定理与导数应用 (3)y=x2 2 解：xE(-0,+o),y=3V元 y不存在的点x=0, X (-0∞，0) 0 (0,+∞) y 不存在 + y y 故：y=xZ在(-∞，0]上单减， ⊕ 在(0，+∞)上单增

解：𝒙 ∈ (−∞, +∞)， 𝒚´ 不存在的点𝒙 = 𝟎, 𝑥 𝑦 ´ 𝑦 故： 𝒚 = 𝟑 𝒙 𝟐在 (−∞, 𝟎]上单减， 在(𝟎, +∞)上单增。 (−∞,0) 0 (0,+∞) − 不存在 + ↘ ↗ （3）𝒚 = 𝟑 𝒙 𝟐 𝑦 ′ = 2 3 3 𝑥

中值定理与导数应用 判定函数单调性的步骤： (1)先求函数的定义域D; (2)求函数的驻点即f'(x)=0,或f'(x1)不存在的点； (3)由D,xo,x1划分区间，判定定理判定： (4)总结

判定函数单调性的步骤： (1)先求函数的定义域D； (2)求函数的驻点即 𝒇′(𝒙𝟎 ) = 𝟎 ,或 𝒇 ′(𝒙𝟏 ) 不存在的点； (3)由𝑫，𝒙𝟎 , 𝒙𝟏划分区间，判定定理判定； (4)总结

中值定理与导数应用 例2： 求下列函数的单调区间。 (1)y=x3-3x 解： x∈(-0∞，+∞)，y=3x2-3, 令y=0, x1=-1,x2=1 X (-∞，-1) 一1 (-1,1) 1 (1,+∞) + 0 0 + y 入 y 函数y=x3-3x,在[-1,1]上单减； 在(-∞，-1)，(1，+0)上单增

例2： 求下列函数的单调区间。 (1) 𝒚 = 𝒙 𝟑 − 𝟑𝒙 解： 𝒙 ∈ (−∞, +∞)， 𝒚′ = 𝟑𝒙𝟐 − 𝟑， 𝒙𝟏 = −𝟏, 𝒙𝟐 = 𝟏 𝑥 𝑦′ 𝑦 (−∞, −1) −1 (−1,1) 1 (1, +∞) + 0 − 0 + ↗ ↘ ↗ 函数𝒚 = 𝒙 𝟑 − 𝟑𝒙， 在[−𝟏, 𝟏]上单减； 在(−∞, −𝟏), (𝟏, +∞)上单增。 令𝒚′ = 𝟎