《高等数学》课程教学课件（讲稿）4-7曲线的渐进线

第七讲 曲线的渐进线

第七讲 曲线的渐进线

中值定理与导数应用 1.曲线的渐近线 定义1：如果曲线y=f(x)上的动点M沿着曲线无限 远离坐标原点时，它与某直线L的距离趋于零，则称 此直线L为曲线y=f(x)的渐进线。 水平渐进线 渐进线 垂直渐进线 斜渐进线

定义1：如果曲线𝒚 = 𝒇(𝒙)上的动点M沿着曲线无限 远离坐标原点时，它与某直线𝑳的距离趋于零，则称 此直线L为曲线𝒚 = 𝒇(𝒙)的渐进线。 水平渐进线 垂直渐进线 斜渐进线 渐进线 1.曲线的渐近线

中值定理与导敛应用 定义2：(1)如果limf(x)=b,则称直线y=b为曲 线y=f(x)的一条水平渐近线。 【x→-∞，x→+o】 (2)如果limf(x)=oo,↓ 则称直线x=x为曲线y=f(x) X→0 的一条铅直渐近线。【x→x,x,】 (3)如果lim[f(x)-ax-b]=0,则称直线y=ax+b 为曲线y=f(x)的一条斜渐近线。 a lim f(x) b=lim[f(x)-ax]. X)00

定义2：(1) 如果𝒍𝒊𝒎 𝒙→∞ 𝒇 𝒙 = 𝒃，则称直线𝒚 = 𝒃为曲 线𝒚 = 𝒇(𝒙)的一条水平渐近线。 【𝒙 → −∞, 𝒙 → +∞】 (2) 如果𝒍𝒊𝒎 𝒙→𝒙𝟎 𝒇 𝒙 = ∞，则称直线𝒙 = 𝒙𝟎为曲线𝒚 = 𝒇(𝒙) 的一条铅直渐近线。 (3) 如果𝒍𝒊𝒎 𝒙→∞ [𝒇 𝒙 − 𝒂𝒙 − 𝒃] = 𝟎，则称直线𝒚 = 𝒂𝒙 + 𝒃 为曲线𝒚 = 𝒇(𝒙)的一条斜渐近线。 𝒂 = 𝒍𝒊𝒎 𝒙→∞ 𝒇(𝒙) 𝒙 , 𝒃 = 𝒍𝒊𝒎 𝒙→∞ [𝒇 𝒙 − 𝒂𝒙]. 【𝒙 → 𝒙𝟎 + , 𝒙𝟎 − 】

中值定理与导数应用 例1：求下列曲线的渐进线， (1)y arctanx 解： lim arctanx = X→+00 lim arctanx X→-00 y=y=一都为y=arctanx的水平渐进线

例1： 求下列曲线的渐进线. 解： (𝟏) 𝒚 = 𝒂𝒓𝒄𝒕𝒂𝒏𝒙 𝑦 = 𝜋 2 , 𝑦 = − 𝜋 2都为𝑦 = 𝑎𝑟𝑐𝑡𝑎𝑛𝑥的水平渐进线。 lim 𝑥→+∞ 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 = 𝜋 2 lim 𝑥→−∞ 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 = − 𝜋 2

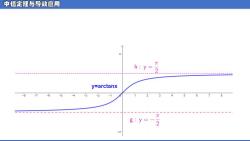
中值定理与导数应用 T h:y= y=arctanx -3 -2 -1 g:y=-2 -I

中值定理与导数应用 (2)y=e-x2 解： lim e-x2 =o X→+00 y=0为y=ex2的水平渐进线。 y=e-x2没有垂直的渐进线

(2) 𝑦 = 𝑒 −𝑥 2 解： lim 𝑥→+∞ 𝑒 −𝑥 2 = 0 𝑦 = 0为𝑦 = 𝑒 −𝑥 2的水平渐进线。 𝑦 = 𝑒 −𝑥 2没有垂直的渐进线

中值定理与导敛应用 1.5 f(x)=ex 0.5 -2.5 -2 -15 -1 -0.5 0 0.5 152 2.5 g:y=0 0.5

中值定理与导数应用 3)y=x+日 解： 1、 lim(x+=oo X→0 x=0为y=x+二的垂直渐近线。 X f(x) a lim 二1 X→00 x b=lim [f(x)-x]=0 X→00 1 y=x为y=x十二的斜渐近线。 X

解： (3) y = 𝑥 + 1 𝑥 𝑦 = 𝑥为𝑦 = 𝑥 + 1 𝑥 的斜渐近线。 lim 𝑥→0 (𝑥 + 1 𝑥 ) = ∞ 𝑎 = lim 𝑥→∞ 𝑓(𝑥) 𝑥 = 1 𝑏 = lim 𝑥→∞ [ 𝑓 𝑥 − 𝑥] = 0 𝑥 = 0为𝑦 = 𝑥 + 1 𝑥 的垂直渐近线

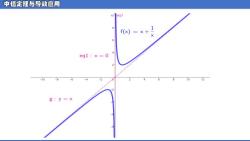
中值定理与导敛应用 1oeq1 8 f(）)=×+ 6 eq1:×=0 10 8 10 2 g:y=x

中值定理与导数应用 1-2x (4)y= +1 x2 1-2x 解： lim +1=1 x→+00 x2 1-2x y=1为y= 1的水平渐进线。 x2 1-2x lim +1=0∞ x→0 x2 x=0为y=1 -2x 2+1的垂直渐进线

(4) 𝑦 = 1 − 2𝑥 𝑥 2 + 1 解： lim 𝑥→+∞ 1 − 2𝑥 𝑥 2 + 1 = 1 𝑦 = 1为𝑦 = 1 − 2𝑥 𝑥 2 − 1的水平渐进线。 lim 𝑥→0 1 − 2𝑥 𝑥 2 + 1 = ∞ 𝑥 = 0为𝑦 = 1 − 2𝑥 𝑥 2 + 1的垂直渐进线