《高等数学》课程教学课件（讲稿）6-5平面图形的面积

第一讲 定积分的应用

第一讲 定积分的应用

高等数学在线开放课程 定积分及其应用 一、定积分的应用 1. 复习引入 2. 定积分在几何上的应用 3. 定积分在物理上的应用

1. 复习引入 3. 定积分在物理上的应用 2. 定积分在几何上的应用 一、定积分的应用

高等数学在线开放课程 定积分及其应用 一、复习引入： 例1：求由连续曲线y=f(x),直线x=a、x=b (α<b)及x轴所围成的平面图形的面积。 a)分 y=fx) b)匀 c)合 X=a x=b d)精 0 a b x

例1：求由连续曲线𝑦 = 𝑓(𝑥)，直线𝑥 = 𝑎、𝑥 = 𝑏 （𝑎 < 𝑏）及𝑥 轴所围成的平面图形的面积。 a) 分 b) 匀 c) 合 d) 精 一、复习引入：

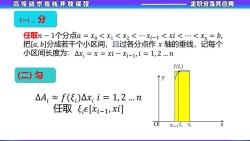
高等数学在线开放课程 定积分及其应用 一)、分 任取n-1个分点a=x0<x1<x2<.xi-1<xi<:<xn三b, 把[a,b]分成若干个小区间，且过各分点作x轴的垂线，记每个 小区间长度为：△x:=x=xi-xi-1,i=1,2.n (二)匀 △A:≈f(5)△x:i=1,2.n 任取：e[xi-1,xi] xi-15i xi

任取𝑛 − 1个分点𝑎 = 𝑥0 < 𝑥1 < 𝑥2 < ⋯ 𝑥𝑖−1 < 𝑥𝑖 < ⋯ < 𝑥𝑛 = 𝑏, 把[𝑎, 𝑏]分成若干个小区间，且过各分点作 𝑥 轴的垂线，记每个 小区间长度为: Δ𝑥𝑖 = 𝑥 = 𝑥𝑖 − 𝑥𝑖−1, 𝑖 = 1, 2 . 𝑛 (二) 匀 （一）、分 O x y Δ𝐴𝑖 ≈ 𝑓(𝜉𝑖 )Δ𝑥𝑖 , 𝑖 = 1, 2 . 𝑛 任取 𝜉𝑖 𝜖[𝑥𝑖−1, 𝑥𝑖] 𝑥𝑖−1 𝑥𝑖 𝑓(𝜉𝑖 ) 𝜉𝑖

高等数学在线开放课程 定积分及其应用 三)合 n 求和： A≈f()Ax= i=1 f(51)△x1+f(52)△x2+.+f(5n)△xn (四)精 入=max{△x1,△x2,.,△xn} A-∑fa=2f()dx

(三) 合 (四) 精 λ= max{∆𝑥1, ∆𝑥2, . , ∆𝑥𝑛} a׬= 𝑏 𝑓 𝑥 𝑑𝑥 𝐴 ≈ ෍ 𝑖=1 𝑛 𝑓 𝜉𝑖 ∆𝑥𝑖 = 𝑓 𝜉1 ∆𝑥1 + 𝑓 𝜉2 ∆𝑥2 + ⋯ + 𝑓 𝜉𝑛 ∆𝑥𝑛 求和： 𝐴 = lim 𝜆→0෍ 𝑖=1 𝑛 𝑓(𝜉𝑖)∆𝑥𝑖

高等数学在线开放课程 定积分及甚应用 二、微元法： (1)根据问题的具体情况，选取积分变量，如x为积分变 量，并确定积分区间[α，b]; 1)选取变量x或y,∈[a,b] (2)设想把区间[a,b]分成n个小区间，取其中任一小区间并 记为[x,x+dx],求出相应于这小区间的部分分量△F的近似 值。如果△F能近似地表示为[a,b]上的一个连续函数在x处 的值f(x)与dx的乘积，就把f(x)dx乘积称为量F的微元且 记作dF,即dF=f(x)dx; 2)微元dF=f(x)dx

二、微元法： 1）选取变量 𝒙或𝒚, ∈ [𝒂, 𝒃] 2）微元d𝐅 = 𝐟 𝐱 𝐝𝐱 (1)根据问题的具体情况，选取积分变量，如x为积分变 量，并确定积分区间 𝑎, 𝑏 ; (2)设想把区间 𝑎, 𝑏 分成n个小区间，取其中任一小区间并 记为 𝑥, 𝑥 + 𝑑𝑥 ,求出相应于这小区间的部分分量∆𝐹的近似 值。如果 ∆𝐹能近似地表示为 𝑎, 𝑏 上的一个连续函数在x处 的值𝑓(𝑥)与𝑑𝑥的乘积，就把𝑓(𝑥)𝑑𝑥乘积称为量𝐹的微元且 记作𝑑𝐹,即𝑑𝐹 = 𝑓 𝑥 𝑑𝑥;

高等邀学在线开放课程 定积分及其应用 3)以所求量F的微元f(x)d 为被积表达式，在区间[a,b]上 作定积分，得F=f(x)dx 3) 写定积分F=fx)dx 即为所求量F的积分表达式。这个方法通常叫做微元法， 应用方向： 平面图形的面积；体积；功；水压力等

这个方法通常叫做微元法． 3）以所求量F的微元 为被积表达式，在区间[a,b]上 作定积分，得𝑭 = ׬�� 𝒃 𝒇 𝒙 𝒅𝒙 f (x)dx 即为所求量 𝑭 的积分表达式. 应用方向： 平面图形的 面积；体积；功；水压力等． 3） 写定积分𝑭 = ׬�� 𝒃 𝒇 𝒙 𝒅𝒙

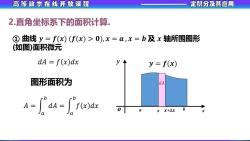
高等数学在线开放课程 定积分及其应用 2.直角坐标系下的面积计算， ①曲线y=f(x)(f(x)>0),x=a,x=b及x轴所围图形 (如图)面积微元 dA =f(x)dx y=f(x) 图形面积为 dA A-心aa=心row 0 xx+△x

2.直角坐标系下的面积计算. ① 曲线 𝒚 = 𝒇(𝒙) (𝒇(𝒙) > 𝟎), 𝒙 = 𝒂 , 𝒙 = 𝒃 及 𝒙 轴所围图形 (如图)面积微元 图形面积为 x y o x 𝒙+∆𝒙 𝑑𝐴 = 𝑓 𝑥 𝑑𝑥 𝒚 = 𝒇(𝒙) 𝑑𝐴 𝐴 = න 𝑎 𝑏 𝑑𝐴 = න 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 a b

高等数学在线开放课程 定积分及其应用 2.直角坐标系下的面积计算. ②由上下两条曲线y=f(x),y=g(x)(f(x)>g(x)及x=a, x=b所围图形（如图）面积微元 dA=[f(x)-g(x)]dx y y=f(x) 图形面积为 dA A-)-ads y=g(x) 0 arx+△x

2.直角坐标系下的面积计算. ② 由上下两条曲线𝒚 = 𝒇(𝒙), 𝒚 = 𝒈(𝒙) (𝒇(𝒙) > 𝒈(𝒙))及𝒙 = 𝒂, 𝒙 = 𝒃 所围图形(如图)面积微元 图形面积为 O 𝒚 = 𝒈(𝒙) y 𝒚 = 𝒇(𝒙) a x 𝒙+∆𝒙 b x 𝑑𝐴 = [𝑓 𝑥 − 𝑔 𝑥 ]𝑑𝑥 𝐴 = න 𝑎 𝑏 𝑑𝐴 = න 𝑎 𝑏 [𝑓 𝑥 − 𝑔(𝑥)]𝑑𝑥 𝑑𝐴

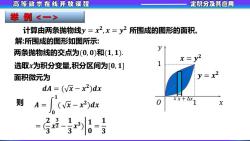
高等数学在线开放课程 定积分及甚应用 举例 计算由两条抛物线y=x2,x=y2所围成的图形的面积。 解：所围成的图形如图所示： 两条抛物线的交点为(0,0)和(1,1). x=y2 选取x为积分变量，积分区间为[0,1] 1 面积微元为 2 =x2 dA=(vx-x2)dx 则 XX+△X A=(vx-x2)dx X 0

举 例 ＜一＞ 计算由两条抛物线𝒚 = 𝒙 𝟐 , 𝒙 = 𝒚 𝟐 所围成的图形的面积。 解:所围成的图形如图所示: 两条抛物线的交点为(𝟎, 𝟎)和(𝟏, 𝟏). 面积微元为 则 选取𝒙为积分变量,积分区间为[𝟎, 𝟏] 𝒅𝑨 = ( 𝒙 − 𝒙 𝟐 )𝒅𝒙 𝑨 = න 𝟎 𝟏 ( 𝒙 − 𝒙 𝟐 )𝒅𝒙 = ( 𝟐 𝟑 𝒙 𝟑 𝟐 − ቤ 𝟏 𝟑 𝒙 𝟑 ) 𝟏 𝟎 = 𝟏 𝟑 𝒚 = 𝒙 𝟐 𝒙 = 𝒚 𝟐 𝑦 𝑂 𝑥 𝑥 𝑥 + ∆𝑥 1 1