《高等数学》课程教学课件（讲稿）6-1定积分概念

第一讲 定积分概念

第一讲 定积分概念

定积分及其应用 一.定积分的概念 ●●● 1.复习引入 2.曲边梯形 3.定积分的概念

1. 复习引入 3. 定积分的概念 2. 曲边梯形 一. 定积分的概念

定积分及其应用 一复习引入 1.古代如何求圆的面积？ 割圆术 a)分 b)匀 c)合 d)精

a) 分 b) 匀 c) 合 d) 精 1. 古代如何求圆的面积？ ————— 割 圆 术 一. 复习引入

定积分及其应用 一.复习引入 对于平面内由任意曲线所围成的封闭图形面积如何计算？ A=? 其面积如何计算？这就是我们这节课将要解决的问题

其面积如何计算？这就是我们这节课将要解决的问题。 对于平面内由任意曲线所围成的封闭图形面积如何计算？ 𝑨 = ？ 一. 复习引入

定积分及其应用 y m 将其置于直角 A=? A 坐标系下考察 B b 任意曲线所围成的平面图形面积归结为两个图形面积之差

A=？ o x y 𝒂 𝒃 𝑩 m n 将其置于直角 坐标系下考察 𝑨 任意曲线所围成的平面图形面积归结为两个图形面积之差

定积分及其应用 二曲边梯形 在直角坐标系中，由连续曲线y=f(x),直线 x=a,x=b(a<b)及x轴所围成的图形，如 图所示。 y=f(x) 曲边 底边 a

y=f (x) a b 在直角坐标系中，由连续曲线𝒚 = 𝒇(𝒙)，直线 𝒙 = 𝒂, 𝒙 = 𝒃(𝒂 < 𝒃)及𝒙 轴所围成的图形，如 图所示。 O x y 底 边 曲 边 二. 曲 边 梯 形

定积分及其应用 引例1：曲边梯形的面积 例1：求由连续曲线y=f(x),直线x=a, x=b(α<b)及x轴所围成的平面图形的面积。 观察与思考 f(x) a)分 b)匀 c)合 d)精

例1：求由连续曲线𝒚 = 𝒇(𝒙)，直线𝒙 = 𝒂, 𝒙 = 𝒃（𝒂 < 𝒃）及𝒙 轴所围成的平面图形的面积。 观察与思考 a) 分 b) 匀 d) 精 引例1：曲边梯形的面积 c) 合

定积分及其应用 (一)分 y=f(x) 任取n-1个分点a=x0<x1< x2<.xi-1<xi<.<Xn=b, 把[a,b]分成若干个小区间， 且过各分点作x轴的垂线，记每 个小区间长度为： △x:=Xi-Xi-1 0 to=a x1 Z2 Ti-1 xi Tn-1 b=Tn x i=1,2.n

  i i x , x −1 Δ𝒙𝒊 = 𝒙𝒊 − 𝒙𝒊−𝟏, 𝒊 = 𝟏, 𝟐 . 𝒏   i i x , x −1 （一）分 任取𝒏 − 𝟏个分点𝒂 = 𝒙𝟎 < 𝒙𝟏 < 𝒙𝟐 < ⋯ 𝒙𝒊−𝟏 < 𝒙𝒊 < ⋯ < 𝒙𝒏 = 𝒃, 把[𝒂, 𝒃]分成若干个小区间， 且过各分点作 𝒙轴的垂线，记每 个小区间长度为:

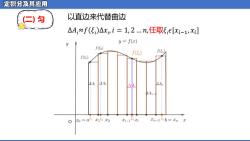
定积分及其应用 (二)匀 以直边来代替曲边 △A:≈f(ξ)△xi=1,2.n,任取5[xi-1vx] y=f(x) f2) f(E) f(En fξ) △A1 △A2 4H. △A 0=a9x15x2 Ti-1Ti In-15b=Tn Z

( 二) 匀 以直边来代替曲边 Δ𝐴𝑖≈𝑓 𝜉𝑖 Δ𝑥𝑖, 𝑖 = 1 , 2 . 𝑛 ,任取 𝜉 𝑖 𝜖 [ 𝑥 𝑖 − 1 , 𝑥 𝑖 ]

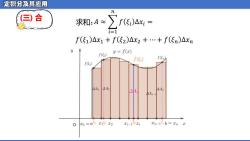
定积分及其应用 n ()合 求和：A≈ ∑f(G)Ax= 7, =1 f(ξ1)△x1+f(52)△x2+.+f(ξn)△xn f(5) y=f(x) f(E) f(E f(5) 4A1 △A2 A 0 0=a1x2 Ti-1siTi In-15b=In T

求和 ： 𝐴 ≈ ෍𝑖=1𝑛 𝑓 𝜉 𝑖 ∆ 𝑥 𝑖 = 𝑓 𝜉 1 ∆ 𝑥 1 + 𝑓 𝜉 2 ∆ 𝑥 2 + ⋯ + 𝑓 𝜉𝑛 ∆ 𝑥 𝑛 ( 三) 合