《高等数学》课程教学课件（讲稿）10-1-1二重积分的概念

第十章 重积分

重积分 第十章 重 积 分

第一讲 二重积分的概念

重积分 第一讲 二重积分的概念

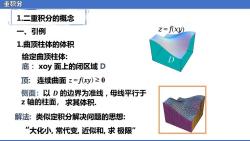
重积分 1.二重积分的概念 一、引例 之=fXy) 1.曲顶柱体的体积 给定曲顶柱体： 底：Xoy面上的闭区域D 顶：连续曲面z=fxy)≥0 侧面：以D的边界为准线，母线平行于 z轴的柱面，求其体积. 解法：类似定积分解决问题的思想： “大化小，常代变，近似和，求极限

重积分 1.二重积分的概念 解法: 类似定积分解决问题的思想: 一、引例 1.曲顶柱体的体积 给定曲顶柱体: ᵉ = ᵈ(ᵉ ,ᵉ ) ≥ ᵼ 底： xoy 面上的闭区域 D 顶: 连续曲面 求其体积. “大化小, 常代变, 近似和, 求 极限” ᵆ = ᵅ(ᵆ ,ᵆ )

重积分 1)“大化小” 用任意曲线网分D为n个区域 z=f(xy) △0A02,.,△0 以它们为底把曲顶柱体分为n个 fn) 小曲顶柱体 2)“常代变” Nk 在每个A0专中任取一点传，刀， 则 △Vk≈f5,n)△ok(k=12,.n) 3)“近似和” v=∑4ve-∑f5,0aox k=1

重积分 ᵆ = ᵅ(ᵆ ,ᵆ ) 1)“大化小” ᵱ ᵴ ᵼ ,ᵱ ᵴ ᵽ ,  ⋯ , ᵱ ᵴ ᵈ 以它们为底把曲顶柱体分为 n 个 2)“常代变” 在每个ᵱ ᵴ ᵈ ( ᵴ ᵈ , ᵳ ᵈ ), 3)“近似和” ᵈ( ᵴ ᵈ , ᵳ ᵈ ) ᵱ ᵇ ᵈ ≈ ᵈ( ᵴ ᵈ , ᵳ ᵈ )ᵱ ᵴ ᵈ (ᵈ = ᵼ ,ᵽ , ⋯ ,ᵈ ) 中任取一点 则 小曲顶柱体 ᵱ ᵴ ᵈ ( ᵴ ᵈ , ᵳ ᵈ )

重积分 4)“取极限” 定义Aok的直径为 λ（△ok)=max{P1P2llP1,P2∈△ok} 令λ=max{(△ok)} z=f(xy) 1≤k≤m v(n) 传 )△0k

重积分 4)“取极限” 令 ᵆ = ᵅ(ᵆ ,ᵆ ) ᵅ( ᵰ ᵅ , ᵰ ᵅ ) ᵮ ᵰ ᵅ ( ᵰ ᵅ , ᵰ ᵅ )

重积分 2.平面薄片的质量 有一个平面薄片，在xoy平面上占有区域D,其面密度为 u(Xy)∈C,计算该薄片的质量M. 若(x,y)三u(常数)，设D的面积为o,则 M=u·6 若(X)非常数，仍可用 “大化小，常代变，近似和，求极限” 解决。 1)"大化小” 用任意曲线网分D为n个小区域△o,A02,.,A0m 相应把薄片也分为小区域

重积分 2. 平面薄片的质量 ᵰ (ᵆ ,ᵆ ) ∈ ᵃ , 度为 则 ᵄ = ᵰ ⋅ ᵰ 若ᵰ (ᵆ ,ᵆ ) 非常数 , 仍可用 其面密 “大化小, 常代变,近似和, 求 极限” 解决. 1)“大化小” ᵮ ᵰ 1 ,ᵮ ᵰ 2 ,  ⋯ , ᵮ ᵰ ᵅ , 相应把薄片也分为小区域 . ᵆ ᵆ

重积分 2)“常代变” 在每个△o中任取一点（传和）， 则第k小块的质量 4Mk≈u5k,刀k)△0k(k=1,2,.n) 3)“"近似和” w-A=6nan 2 2 k=1 4)“取极限" 令λ=max{(△ok)} (信k) 1≤k≤n M=∑A(《,k)as k=1

重积分 2)“常代变” 中任取一点( ᵰ ᵅ , ᵰ ᵅ ), 3)“近似和” 4)“取极限” ᵮ ᵰ ᵅ ( ᵰ ᵅ , ᵰ ᵅ ) ᵮ ᵄ ᵅ ≈ ᵰ ( ᵰ ᵅ , ᵰ ᵅ )ᵮ ᵰ ᵅ    (ᵅ = 1,2, ⋯ ,ᵅ ) 则第 k 小块的质量 ᵆ ᵆ

重积分 两个问题的共性： (1)解决问题的步骤相同 “大化小，常代变，近似和，取极限” (2)所求量的结构式相同 曲顶柱体体积： V=》f(5,k)△ok k=1 平面薄片的质量： M=lim〉u(5k,k)△o k=1

重积分 两个问题的共性： (1) 解决问题的步骤相同 (2) 所求量的结构式相同 “大化小, 常代变, 近似和,取极限” 曲顶柱体体积: 平面薄片的质量:

重积分 2.二重积分的定义及可积性 定义：设f(x,y)是定义在有界区域D上的有界函数， 将区域D任意分成n个小区域，Ao(k=1,2,.,n), 任取一点（传，”∈Ak, 若存在一个常数1，使 m 记作 I=l》f(5k)△oe k= 则称fxy) 可积称I为fy) 在D上的二重积分， 积分和 积分表达式 f (x,y)do x,y称为积分变量 积分域 被积函数 面积元素

重积分 2.二重积分的定义及可积性 定义: ᵮ ᵰ ᵅ  (ᵅ = 1 , 2 ,  ⋯  , ᵅ ), 任取一点 ( ᵰ ᵅ , ᵰ ᵅ ) ∈ᵮ ᵰ ᵅ  , 可积 , 则称ᵅ(ᵆ ,ᵆ ) 称ᵃ为ᵅ(ᵆ ,ᵆ ) 在D上的二重积分. 积分和 积分域 被积函数 积分表达式 面积元素 记作

重积分 如果∫(x,y)在D上可积，可用平行坐标轴的直线来划 分区域D,这时Aok=△Xk4yk,因此面积元素da也常 记作dxdy,二重积分记作 f(x,y)dxdy. 引例1中曲顶柱体体积： v-do-.xy 引例2中平面薄板的质量： M=a(ya=八a6 x.yjdxdy

重积分 引例1中曲顶柱体体积: 引例2中平面薄板的质量: 也常 二重积分记作 ᵮ ᵰ ᵅ = ᵮ ᵆ ᵅ ᵮ ᵆ ᵅ 这时 , 因此面积元素 可用平行坐标轴的直线来划 记作