《高等数学》课程教学课件（讲稿）12-1-3常数项级数的概念与性质

第三讲 常数项级数的敛散性

无 穷 级 数 第三讲 常数项级数的敛散性

无穷级敛 1.常数项级数的敛散性 拆项相消法 (1) =1-1 1 n(n+1)n +1 2)=- 1 (3)lm(1+3=lm(n+1)-lmn (4)lm(1-之)=m(n+1)+ln(n-1)-2lnn

无 穷 级 数 1.常数项级数的敛散性 拆项相消法

无穷级数 举例 例1.判定下列级数的敛散性， 1 1 1 12+23+ n(n+1) 十. 1 解： n 11 n(m+1)nn+1 111 11 Sn=1-2+23+.+ =1- nn+1 n+1 limSn=1,所以该级数收敛， n→0o

无 穷 级 数 举例 例1. 判定下列级数的敛散性. 解： 所以该级数收敛

无穷级数 举例 例2.判定下列级数的敛散性， 00 .n+1 n n=1 n+1 解：un=ln一=ln(n+1)-lmn Sn in2-in1 In3-in2 in4-in3+In(n+1)-Inn =ln(n+1) limSn=oo,所以该级数发散. →00

无 穷 级 数 举例 例2. 判定下列级数的敛散性. 解： = ᵈᵈ (ᵅ + 1) 所以该级数发散

无穷级数 举例 例3.判定级数 m(1-n2)1 的敛散性 m=2 解：4：=a1-)=aa+)+an-)-2mn Sn=3+lm1-2m2]+[lm4+lm2-23] +[ln5+3-2ln4+tnn+ln(n-2)+ 2ln-1]+[n(n+1)+lm-1)-2lnu n+1_-m2 Sn=In(n+1)-Inn-In2=In- limSn=-ln2,所以该级数收敛， n→0∞

无 穷 级 数 举例 例3. 判定级数 的敛散性. 解： 所以该级数收敛

无穷级敛 级数收敛的必要条件 收敛级数〉 un,必有limun=0. n→0∞ n=1 若级数的一般项不趋于0，则级数必发散. (1) lim (1+ -)n =e n→∞ nπ (2) lim sin 3 极限不存在，3也可写成别的整数， n-co (3) 4n+1>1,u1>0 un

无 穷 级 数 级数收敛的必要条件 收敛级数 必有 若级数的一般项不趋于0 , 则级数必发散. 极限不存在，3也可写成别的整数

无穷级数 举例 enn! 例4.判定级数 nn 的敛散性. n=1 emn! 解：山n=nh，山+1= en+1(n+1)月 (n+1)n+1 4+1= enti(n+1)!nn e (1+ ->1 un (n+1)ntienn! un+1>un,u=e>1 所以u单增，且第一项大于1， lim un≠0，该级数发散. n→00

无 穷 级 数 举例 例4. 判定级数 的敛散性. 解： 该级数发散

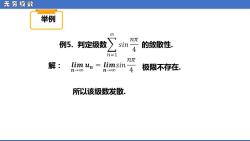
无穷级数 举例 00 nT元 例5.判定级数 的敛散性。 n=1 nπ 解： lim un=limsin4 n→oo n→0o 极限不存在 所以该级数发散

无 穷 级 数 举例 例5. 判定级数 的敛散性. 解： 极限不存在. 所以该级数发散

无穷级数 基础练习 1. 下列哪个级数是收敛的？ (C) 00 n元 A. sin n=1 00 B 00 7 V n(n+2) 00 1 D 3n n=1

无 穷 级 数 基础练习 1. 下列哪个级数是收敛的？ √ (ᵆ )

无穷级敛 基础练习 2. 下列哪个级数是发散的？ (A) 00 A (Vn+1-n) n=1 00 1 B. 2 V3 00 1 C. n(n+1) 00 1 D (2n-1)(2n+1)

无 穷 级 数 基础练习 2. 下列哪个级数是发散的？ √ (ᵆ )