《高等数学》课程教学课件（讲稿）6-6旋转体体积

第二讲 旋转体的体积

第二讲 旋转体的体积

定积分及其应用 一、定积分的应用 1、复习平面图形面积的求法 2、定积分在几何上的应用 3、定积分在物理上的应用

1、 复习平面图形面积的求法 3、 定积分在物理上的应用 2、 定积分在几何上的应用 一、定积分的应用

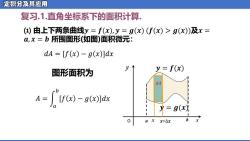
定积分及其应用 复习.1.直角坐标系下的面积计算. (1)由上下两条曲线y=f(x),y=g(x)f(x)>g(x)及x= α，x=b所围图形（如图）面积微元： dA=[f(x)-g(x)]dx 图形面积为 y=f(x) dA A=If(x)-g(x)ldx =g@i arx+△x

复习.1.直角坐标系下的面积计算. ⑴ 由上下两条曲线𝒚 = 𝒇(𝒙), 𝒚 = 𝒈(𝒙) (𝒇(𝒙) > 𝒈(𝒙))及𝒙 = 𝒂, 𝒙 = 𝒃 所围图形(如图)面积微元： 图形面积为 O 𝒚 = 𝒈(𝒙) y 𝒚 = 𝒇(𝒙) a x 𝒙+∆𝒙 b x 𝑑𝐴 = [𝑓 𝑥 − 𝑔 𝑥 ]𝑑𝑥 𝐴 = න 𝑎 𝑏 [𝑓 𝑥 − 𝑔(𝑥)]𝑑𝑥 𝑑𝐴

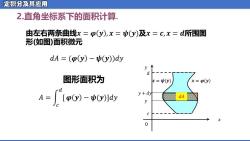
定积分及其应用 2.直角坐标系下的面积计算， 由左右两条曲线x=p(y),x=(y)及x=c,x=d所围图 形（如图）面积微元 dA =((y)-v(y))dy y d 图形面积为 =(y) x=o(y) A=[00y-6]a y+dy dA X

2.直角坐标系下的面积计算. 由左右两条曲线𝒙 = 𝝋 𝒚 , 𝒙 = 𝝍(𝒚)及𝒙 = 𝒄, 𝒙 = 𝒅所围图 形(如图)面积微元 图形面积为 O 𝑥 𝑦 𝑑 𝑦 + 𝑑𝑦 𝑦 𝑐 𝒙 = 𝝍(𝒚) 𝒙 = 𝝋 𝒚 𝑑𝐴 = (𝝋 𝒚 − 𝝍(𝒚))𝑑𝑦 𝐴 = න 𝑐 𝑑 [ 𝝋 𝒚 − 𝝍(𝒚)]𝑑𝑦 𝑑𝐴

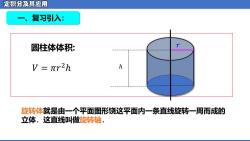
定积分及其应用 复习引入： 圆柱体体积： V=πr2h h 旋转体就是由一个平面图形饶这平面内一条直线旋转一周而成的 立体.这直线叫做旋转轴

一、复习引入： 圆柱体体积: ℎ 𝑟 旋转体就是由一个平面图形饶这平面内一条直线旋转一周而成的 立体．这直线叫做旋转轴． 𝑉 = 𝜋𝑟 2ℎ

定积分及其应用 圆柱 环形圆柱 圆锥 圆台 球体 1 V=πr2h 4 V= V=3m3 V=π(R-r)2h V= 3π(R2+Rr+r2)h

圆柱 环形圆柱 圆锥 圆台 球体 𝑉 = 𝜋𝑟 2ℎ 𝑉 = 𝜋(𝑅 − 𝑟) 2ℎ 𝑉 = 1 3 𝜋𝑟 2ℎ 𝑉 = 1 3 𝜋(𝑅 2+𝑅𝑟 + 𝑟 2 )ℎ 𝑉 = 4 3 𝜋𝑟 3

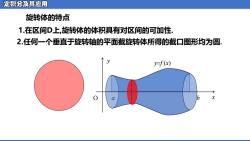
定积分及其应用 旋转体的特点 1.在区间D上，旋转体的体积具有对区间的可加性. 2.任何一个垂直于旋转轴的平面截旋转体所得的截口图形均为圆. f() X

旋转体的特点 1.在区间D上,旋转体的体积具有对区间的可加性. 2.任何一个垂直于旋转轴的平面截旋转体所得的截口图形均为圆. O a b x y y=f (x)

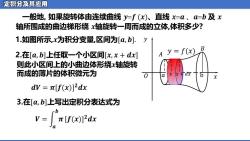
定积分及其应用 一般地，如果旋转体由连续曲线y=f(x)、直线x=a、a=b及x 轴所围成的曲边梯形绕x轴旋转一周而成的立体，体积多少？ 1如图所示，x为积分变量，区间为[a,b.y 、B 2.在[a,b]上任取一个小区间[x,x+dx] A y=f(x) 则此小区间上的小曲边体形绕x轴旋转 而成的薄片的体积微元为 dV=π[f(x)]2dx 3.在[a,b]上写出定积分表达式为 v=πfo]2dx

一般地, 如果旋转体由连续曲线 𝒚=𝒇 (𝒙)、直线 𝒙=𝒂 、𝒂=𝒃 及 𝒙 轴所围成的曲边梯形绕 𝒙轴旋转一周而成的立体,体积多少? 1.如图所示,𝒙为积分变量,区间为[𝒂, 𝒃]. 2.在[𝒂, 𝒃]上任取一个小区间[𝒙, 𝒙 + 𝒅𝒙] 则此小区间上的小曲边体形绕𝒙轴旋转 而成的薄片的体积微元为 3.在[𝒂, 𝒃]上写出定积分表达式为 𝑎 𝑥 b 𝑥 𝑦 𝑥 + 𝑑𝑥 𝐵 𝐴 𝑂 𝑦 = 𝑓(𝑥) 𝒅𝑽 = 𝝅[𝒇(𝒙)] 𝟐𝒅𝒙 𝑽 = න 𝒂 𝒃 𝝅[𝒇(𝒙)] 𝟐𝒅𝒙

定积分及其应用 举例 连接坐标原点0及点P(h,r)的直线、直线x=h及x轴围成一 个直角三角形.将它绕x轴旋转构成一个底半径为r、高为h的圆锥 体。计算这圆锥体的体积。 解： 直线0P方程为 1 y=五x 取积分变为量x,xe[0,h] 在[0，h]上任取一个小区间[x,x+dx] 以dx为底的窄曲边梯形绕x轴旋转而成的薄片体 积微元为： dw=π听2dx 所求回锥体的体积为：V=哈π哈2dr-茫日-写m2h 10

举 例 ＜一＞ 连接坐标原点𝑶及点𝑷(𝒉，𝒓)的直线、直线𝒙=𝒉 及𝒙 轴围成一 个直角三角形．将它绕𝒙轴旋转构成一个底半径为𝒓、高为𝒉的圆锥 体。计算这圆锥体的体积。 x y O x h r y = h r 解: 直线 𝑶𝑷方程为 以𝒅𝒙为底的窄曲边梯形绕𝒙轴旋转而成的薄片体 积微元为： 取积分变为量𝒙，𝒙𝝐[𝟎, 𝒉] 所求圆锥体的体积为: 在[𝟎, 𝒉]上任取一个小区间[𝒙, 𝒙 + 𝒅𝒙] 𝒅𝑽 = 𝝅[ 𝒓 𝒉 𝒙] 𝟐𝒅𝒙 𝑥 𝑥 + 𝑑𝑥 ��׬ = �� 𝒉 𝝅( 𝒓 𝒉 𝒙) 𝟐𝒅𝒙 𝑦 = 𝑟 ℎ 𝑥 = 𝝅𝒓 𝟐 𝟑𝒉𝟐 𝒙 𝟑 | 𝒉 𝟎 = 𝟏 𝟑 𝝅𝒓 𝟐𝒉

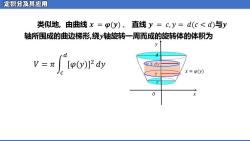
定积分及其应用 类似地，由曲线x=p(y)、直线y=c,y=d(c<d)与y 轴所围成的曲边梯形，绕y轴旋转一周而成的旋转体的体积为 y v=π.[p0dy +dy x=o(y) 0 X

类似地, 由曲线 𝒙 = 𝝋(𝒚) 、 直线 𝒚 = 𝑐, 𝑦 = 𝑑(𝑐 < 𝑑)与𝒚 轴所围成的曲边梯形,绕𝒚轴旋转一周而成的旋转体的体积为 𝑉 = 𝜋 න 𝑐 𝑑 [𝜑(𝑦)] 2 𝑑𝑦 𝑦 𝑂 𝑥 𝑐 𝑑 𝑥 = 𝜑(𝑦) 𝑦 𝑦 + 𝑑𝑦