《高等数学》课程教学课件（讲稿）3-1导数概念

导数与微分 复习： sinx sin2 (1)1im A:1 B:2 C:0 D: x→2 x2 4 sinx sin2 (2)lim A:1 B:2 C:0 D: X→0 4 sinx sin2 (3)lim 二 A:1 B:2 C:0 D: X→00 x 4 (④)f)=在x=0是 A:第一类间断点B:第二类间断点C:第三类间断点D:连续点 (5)f(x)=n在x=2,是 A:第一类间断点B:第二类间断点C:第三类间断点D:连续点

复习： (𝟏) 𝐥𝐢𝐦 𝒙→𝟐 𝒔𝒊𝒏𝒙 𝒙 𝟐 = 𝑨: 𝟏 𝑩: 𝟐 𝑪: 𝟎 𝑫: 𝒔𝒊𝒏𝟐 𝟒 (𝟐) 𝐥𝐢𝐦 𝒙→𝟎 𝒔𝒊𝒏𝒙 𝒙 = 𝑨: 𝟏 𝑩: 𝟐 𝑪: 𝟎 𝑫: 𝒔𝒊𝒏𝟐 𝟒 (𝟑) 𝐥𝐢𝐦 𝒙→∞ 𝒔𝒊𝒏𝒙 𝒙 = 𝑨: 𝟏 𝑩: 𝟐 𝑪: 𝟎 𝑫: 𝒔𝒊𝒏𝟐 𝟒 𝟒 𝒇 𝒙 = 𝒔𝒊𝒏𝒙 𝒙 在𝒙 = 𝟎,是 𝑨:第一类间断点 𝑩:第二类间断点 𝑪: 第三类间断点 𝑫:连续点 𝟓 𝒇 𝒙 = 𝒔𝒊𝒏𝒙 𝒙 在𝒙 = 𝟐,是 𝑨:第一类间断点 𝑩:第二类间断点 𝑪: 第三类间断点 𝑫:连续点

第一讲 导数概念

第一讲 导数概念

导数与微分 两个引例 1、变速直线运动的瞬时速度 2、平面曲线的切线斜率

两个引例 1、变速直线运动的瞬时速度 2、平面曲线的切线斜率

导数与微分 例1：设某物体作变速直线运动，在[0，t]内所走过 的路程s=s(t)(t>0),求物体在时刻to时的瞬时速度。 解：平均速度 s(to)s(t+△t) 匀 S 人一一t V= 0 to to+△t △s=s(to+△t)-S(to) l△t很小，在[to,to+△t]上 物体的运动近似看作匀速直线运动。 精 取极限，lim △S v(to) △→0△t

例1：设某物体作变速直线运动，在[𝟎, 𝒕]内所走过 的路程𝒔 = 𝒔(𝒕)(𝒕 > 𝟎),求物体在时刻𝒕𝟎时的瞬时速度。 解： t 0 𝑡0 𝑡0 +△t 𝑠(𝑡0 ) 𝑠(𝑡0 +△ 𝑡) △ 𝒔 = 𝒔(𝒕𝟎 +△ 𝒕) − 𝒔(𝒕𝟎 ) 平均速度 v = s t   |△ 𝒕|很小，在[𝒕𝟎 , 𝒕𝟎 +△ 𝒕]上， 物体的运动近似看作匀速直线运动。 取极限， 0 lim t s t  →  =  𝒗(𝒕𝟎 精 ) 匀

导数与微分 2.平面曲线的切线问题 割线 切线 瀑 X

2. 平面曲线的切线问题 切线割线 𝑥 𝑦𝑂 误识

导数与微分 47 31 2 D E -1 2 y=sinx

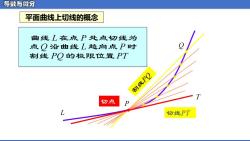
导数与微分 平面曲线上切线的概念 曲线L在点P处点切线为 点Q沿曲线L趋向点P时 割线PQ的极限位置PT 割线PQ T 切点 D 切线PT

平面曲线上切线的概念 L P • Q • • • • • T 切线PT 切点 • PQ PT Q L P L P 割线 的极限位置 点 沿曲线 趋向点 时 曲线 在点 处点切线为

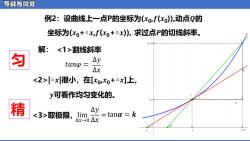
导数与微分 例2：设曲线上一点P的坐标为(xo,f(xo),动点Q的 坐标为(xo+△x,f(xo+△x),求过点P的切线斜率。 解：割线斜率 匀 tang △y △X △x很小，在[xoxo+△x]上， y可看作均匀变化的。 精 取极限，imy=tana=k △x-0△X

例2：设曲线上一点P的坐标为(𝒙0 ,𝒇(𝒙0 )),动点𝑸的 坐标为(𝒙0+△𝒙,𝒇(𝒙0+△𝒙)), 求过点𝑷的切线斜率。 解： 割线斜率 |△𝒙|很小，在[𝒙0 ,𝒙0+△𝒙]上， 精 取极限， tan𝜶 = 𝒌 匀 𝒚可看作均匀变化的。 lim ∆𝑥→0 ∆𝑦 ∆𝑥 = 𝑡𝑎𝑛𝜑 = Δ𝑦 Δ𝑥

导数与微分 导数定义： 定义1： (1)设函数y=f(x)在xo点及其近旁有定义； (2)当x由xo一→xo+△x;而y由f(xo)一f(xo+△x)时， 函数增量为△y=f(xo+△x)-f(xo); (3)若 存在，则称函数y=f(x)在x点可导。 记： f'(x), y'lx=xo dy df(x) dx dx x=xo

(1)设函数𝒚 = 𝒇(𝒙) 在𝒙0点及其近旁有定义； 则称函数𝒚 = 𝒇(𝒙) 在𝒙0点可导。 定义1： (2)当𝒙由𝒙0→𝒙0+△𝒙；而𝒚由𝒇(𝒙0 )→𝒇(𝒙0+△𝒙)时， (3)若 存在， 记： 𝒇 ′(𝒙𝟎 ), lim ∆𝑥→0 ∆𝑦 ∆𝑥 函数增量为△𝒚=𝒇(𝒙𝟎 +△ 𝒙) − 𝒇(𝒙𝟎 )； 导数定义: 𝑦 ′ |𝑥=𝑥0 ቤ 𝑑𝑦 𝑑𝑥 𝑥=𝑥0 ቤ 𝑑𝑓(𝑥) 𝑑𝑥 𝑥=𝑥0

导数与微分 f'(xo)=lim △y = f(xo+△x)-f(xo) lim △x-→0△X △X→0 △X 令△x=t, f(xo +t)-f(xo) f'(xo)=lim t→0 t f'(xo)=lim f(x0+2△x)-f(xo) 令2△x=t, △X→0 2△X 令x0+△x=x,f'(xo)=lim f(x)-f(xo) X→X0 x-xo

𝑓 ′(𝑥0 ) = 令△𝑥 = 𝑡, 令2 △ 𝑥 = 𝑡, 令𝑥0 +△ 𝑥 = 𝑥, 𝑓 ′(𝑥0 ) 𝑓 ′(𝑥0 ) 𝑓 ′(𝑥0 ) lim ∆𝑥→0 ∆𝑦 ∆𝑥 = lim ∆𝑥→0 𝑓 𝑥0 + ∆𝑥 − 𝑓(𝑥0) ∆𝑥 = lim 𝑡→0 𝑓 𝑥0 + 𝑡 − 𝑓(𝑥0) 𝑡 = lim ∆𝑥→0 𝑓 𝑥0 + 2∆𝑥 − 𝑓(𝑥0) 2∆𝑥 = lim 𝑥→𝑥0 𝑓(𝑥) − 𝑓(𝑥0) 𝑥 − 𝑥0