《高等数学》课程教学课件（讲稿）5-1-1反正弦函数

数学（一) 第五章：反三角函数

反三角函数 数学（一） 第五章：反三角函数

第一讲： 反正弦函数的图像 主讲人：卢自娟

反三角函数 第一讲： 反正弦函数的图像 主讲人：卢自娟

反三角函数 引例 当sina= 时， 你能求出满足等式的角a吗？ 显然，sing- 除了a=时，你还能找出满足等式的其它角α吗？ sin(2km+爱=2(k∈Z刀， 如果限定α在一个周期[0,2π]上，此时只有一个角 满足条件吗？ 5π1 6=2 sin=

反三角函数 引例

反三角函数 引例 如何限定角的范围，才能达到只有一个角 满足方程？ sina= [- f(x)=sin(x) π3π [22 C 3π 2

反三角函数 引例 [  − ᵰ 2 , ᵰ 2  ]

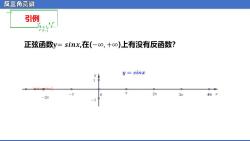
反三角函数 引例 正弦函数y=sinx,在(-oo,+o)上有没有反函数？ y=sind 0 0 -T 0 2n 3π 4TT x -2T

反三角函数 引例

反三角函数 1.反正弦函数 定义1把正弦函数y=sinx,x∈[-，]的反函数 叫做反正弦函数，记作y=arcsinx或y=sin1x. (1)定义域D=[-1,1] (2)值域M=[-271 (3)公式sin(arcsin x)=x,x∈[-1,1] arcsin(-x)=-arcsinx ,x E [-1,1]

反三角函数 1.反正弦函数

反三角函数 2.反正弦函数的图像 y=sinx.xe[ π π X 2 0 4 4 y y=arcsinx 2 y=X sinx -1 √2 0 2 1 2 y=arcsinx,x∈[-1,1] V2 π-1 0 1 X -1 0 √2 1 2 2 2 -1 f(x)=sin(x) 元 π π π arcsinx 0 2 4 4 2 2 22

反三角函数 2. 反正弦函数的图像 0 1 0 1

反三角函教 3.反正弦函数的性质 y=arcsinx,x∈[-1,1] (4)单调性 单调递增 y=arcsinx 2 (5)有界性 有界 (6)奇偶性 奇函数 (7)周期性 没有周期性

反三角函数 3. 反正弦函数的性质 (4) 单调性 (5) 有界性 (6) 奇偶性 (7) 周期性 单调递增 有界 奇函数 没有周期性

反三角函数 4.反正弦函数值 π atsin 0=0 arcsin 6 acin 1= 26 aresin(-2) π = 3 3 arcsin 2 3 V2 V2 aresin(-2) 4 arcsin 2 4 ain(-1)=- arsin 1=匹 2 2

反三角函数 4. 反正弦函数值 ᵈᵉᵈᵉᵈᵈ ᵼ = ᵼ ᵈᵉᵈᵉᵈᵈ ᵼ ᵽ = ᵴ ᵽ ᵈᵉᵈᵉᵈᵈ ᵼ = ᵴ ᵽ ᵈᵉᵈᵉᵈᵈ ( − ᵼ ) = − ᵴ ᵽ

反三角函数 思考 1.y=sinx,x∈[-，]与y=sinx一样吗？ 2.y=sinx,x∈[2，]有反函数吗？

反三角函数 思考