《高等数学》课程教学课件（讲稿）1-7复合函数与初等函数2

第七讲 复合函数 主讲人：卢自娟

函数、极限与连续 第七讲 复合函数 主讲人：卢自娟

还数、极限与连续 复习引入 判断题： (1)y=sin2x是基本初等函数。 X (2)y=Vx2是基本初等函数

函数、极限与连续 复习引入 判断题 ： ×√

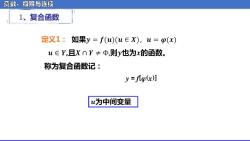
逐数、极限与连续 1、复合函数 定义1：如果y=f(u)(u∈X),u=p(x) u∈Y,且X∩Y≠Φ，则y也为x的函数。 称为复合函数记： y =flo(x)] u为中间变量

函数、极限与连续 称为复合函数记： 定义1： ᵉ = ᵈ[ᵴ (ᵉ )] 1、复合函数

还数、极限与连续 例1.下列哪些函数组合可构成复合函数。 (1)y=sinu,u=5x+8 =n（5x+8 (2)y=Vu,u=x2+2 y=Vx2+2 (3)y=V元，u=-x2-1 X(D=Φ) (4)y arcsinu ,u=x2+6 X (5)y=arcsinu,u=1-x2 y=ain（1-x 练习(6)y=arcsinu,u=1+2x

函数、极限与连续 例1. 下列哪些函数组合可构成复合函数。 ᵉ = ᵉᵈᵈ ( ᵽ ᵉ + ᵽ ) ⅹ ᵉ = ᵈᵉᵈᵉᵈᵈ ( ᵼ − ᵉ ᵽ )

函数、极限与连续 例2.求下列复合函数。 (1)y=u2,u=cosx y (cosx)2=cos2x (2)y=vu,u=sinx y vsinx (3)y=Vu,u=1-x2 y=√1-x2 (4)y arcsinu ,u=2x y=auin 2x (5)y=u3,u=1-x2 y=(1-x2)3

函数、极限与连续 例2. 求下列复合函数。 ᵉ = ᵈᵉᵈᵉᵈᵈ ᵽ ᵉ

还数、极限与连续 例3.求下列函数的复合结构。 (1)y sin2x (2)y sin5x =(sinx·(sinx) =(sinx)2 解：「y=u2 解：「yiu u sink u=5x 由外向内，逐层复合，允许多项式

函数、极限与连续 例3. 求下列函数的复合结构。 解： ᵉ = ᵉ ᵽ ᵉ = ᵉᵈᵈᵉ 解： ᵉ = ᵉᵈᵈᵉ ᵉ = ᵽ ᵉ 由外向内，逐层复合，允许多项式

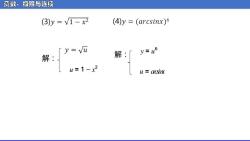
函数、极限与连续 (3)y=V1-x2 (4)y (arcsinx)6 7, 解：「 y=u

函数、极限与连续 解： ᵆ = 1 − ᵆ 2 解： ᵆ = ᵄᵅᵅᵆᵅᵅᵆ ᵆ = ᵆ 6

还数、极限与连续 练习找出下列函数的基本初等函数类型。 (1)y=(1+x3)5 (2y=tam(2x+ 6 (3)y sinvx (4)y=ex2 (5)y=(2x+5)4 (6y=aB(4-3x) (7y=n(1+x (8)y=e-3x2 (9)y ada (10)y =(arctanx)2

函数、极限与连续 练习:找出下列函数的基本初等函数类型。 (ᵽ )ᵉ = ᵉᵈᵈ (ᵽ ᵉ + ᵴ ᵽ ) (ᵽ )ᵉ = ᵈᵉᵉ (ᵽ − ᵽ ᵉ ) (7)ᵆ = ᵈᵈ (ᵼ + ᵉ ᵽ ) (9)ᵆ = ᵈᵉᵈᵉᵈᵈ ᵈ ᵉ

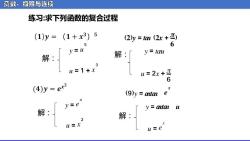
丞数、极限与连续 练习：求下列函数的复合过程 (1)y=(1+x3)5 (2y=tm(2x+匹) 5 6 y=u 解： y tau u=2x+ 6 (4)y=ex2 (9)y ada e y=e y ada u u=e

函数、极限与连续 练习:求下列函数的复合过程 (ᵽ )ᵉ = ᵉᵈᵈ (ᵽ ᵉ + ᵴ ᵽ ) 解： ᵆ = ᵆ 5 ᵆ = 1 + ᵆ 3 解： ᵆ = 2ᵆ + ᵰ 6 ᵆ = ᵆᵄᵅᵆ 解： ᵆ = ᵅ ᵆ ᵆ = ᵆ 2 (9)ᵆ = ᵈᵉᵈᵉᵈᵈ ᵈ ᵉ 解： ᵆ = ᵈᵉᵈᵉᵈᵈ ᵉ ᵆ = ᵅ ᵆ

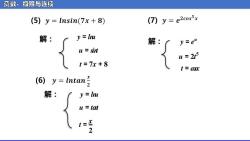
还数、极限与连续 (5)y Insin(7x+8) (7)y=e2cos5x y In 解： y=e" u sint u 2f t=7x+8 t=ax (6)y=intan月 { y=lu u tat t= 2

函数、极限与连续 解： ᵉ = ᵈᵈᵉ ᵉ = ᵉᵈᵈᵉ 解： ᵉ = ᵽ ᵉ + ᵽ ᵉ = ᵉᵈᵈᵉ ᵉ = ᵉ ᵽ ᵉ = ᵈᵈᵉ 解： ᵉ = ᵈ ᵉ ᵉ = ᵽ ᵉ ᵽ ᵉ = ᵈᵉᵉᵉ