《高等数学》课程教学课件（讲稿）2-6-1两个重要的极限

仙 第九讲 两个重要的极限

第九讲 两个重要的极限

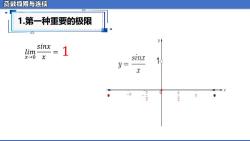
函数极限与连续 1第一种重要的极限 sinx lim 1 X→0 sinx y= 1日 x 2 -2 T

𝑙𝑖𝑚 𝑥→0 𝑠𝑖𝑛𝑥 𝑥 = 1.第一种重要的极限 1

函数极限与连续 inx lim =1 x→0 这只限于分析，计算步 骤里不允许出现此式 ● 分析： 1类型：8型 2.变形： lim父=li 1 =1 x0sinx】 X→0 3形似： lim 二1 sinu u→0 u 故： lim sinf(x)=1 fx)→0f(x) lim f0=1 f(x)→0sinf(x)

分析： 1.类型：𝟎 𝟎 型 2.变形： 𝒍𝒊𝒎 𝒙→𝟎 𝒙 𝒔𝒊𝒏𝒙 = 3.形似： 𝒍𝒊𝒎 𝒖→𝟎 𝒔𝒊𝒏𝒖 𝒖 = 𝟏 故： 𝒍𝒊𝒎 𝒇(𝒙)→𝟎 𝒔𝒊𝒏𝒇(𝒙) 𝒇(𝒙) = 𝟏 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝒙 𝒙 = 𝟏 𝒍𝒊𝒎 𝒙→𝟎 𝟏 𝒔𝒊𝒏𝒙 𝒙 = 𝟏 𝒍𝒊𝒎 𝒇(𝒙)→𝟎 𝒇(𝒙) 𝒔𝒊𝒏𝒇(𝒙) = 𝟏 这只限于分析，计算步 骤里不允许出现此式

函数极限与连续 例1：求下列函数的极限。 (1)lim sin2x ◆分母x→0，分子sin2x→0 →0 解：原式=lim sin2x ×2 X→0 2x sin2x 2×lim X→0台2x→0 2x→0 2x u 2x 2lim u sinu=2x1=2 u-→0

例1： 求下列函数的极限。 (1) 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝒙 解：原式= 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 = 2× 𝒍𝒊𝒎 𝟐𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 = 2𝒍𝒊𝒎 𝒖→𝟎 𝒔𝒊𝒏𝒖 𝒖 = 𝟐ⅹ1=2 𝒖 = 𝟐𝒙 分母𝑥 → 0, 分子𝑠𝑖𝑛 2𝑥 → 0 ×2 𝑥 → 0 ⇔ 2𝑥 → 0

函数极限与连续 (2)lim-i x-0 sin3x 解：原式=lim 3X1 x→0sin3x3 1 ×lim 3x 3 3x→0sin3x X→0台3X→0 u 3x = 久2 u u→0sinu ×1=

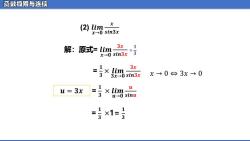
(2) 𝒍𝒊𝒎 𝒙→𝟎 𝒙 𝒔𝒊𝒏𝟑𝒙 解：原式= 𝒍𝒊𝒎 𝒙→𝟎 𝟑𝒙 𝒔𝒊𝒏𝟑𝒙 = 𝟏 𝟑 × 𝒍𝒊𝒎 𝟑𝒙→𝟎 𝟑𝒙 𝒔𝒊𝒏𝟑𝒙 = 𝟏 𝟑 ×1= 𝟏 𝟑 = 𝟏 𝟑 × 𝒍𝒊𝒎 𝒖→𝟎 𝒖 𝒔𝒊𝒏𝒖 𝒖 = 𝟑𝒙 × 𝟏 𝟑 𝑥 → 0 ⇔ 3𝑥 → 0

函数极限与连续 sin2x (1)lim (2)lim- X→0 x-0 sin3x 解：原式=lim sin2x ×2 2x 解：原式=lim 3x x→0 x→0sin3x 3 =1×2=2 =1× = 1-3 x→0台kx(k≠0)→0

𝒙 → 𝟎 ⇔𝒌𝒙(𝒌 ≠ 𝟎) → 𝟎 (1) 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝒙 解：原式= 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 ×2 = 𝟏 × 2=2 (2) 𝒍𝒊𝒎 𝒙→𝟎 𝒙 𝒔𝒊𝒏𝟑𝒙 解：原式= 𝒍𝒊𝒎 𝒙→𝟎 𝟑𝒙 𝒔𝒊𝒏𝟑𝒙 × 𝟏 𝟑 = 𝟏 × 𝟏 𝟑 = 𝟏 𝟑

函数极限与连续 (3)lim sin2x (4)lim sin2x x→0 3x x→0sin3x 解：原式= 1lim sin2x ×2 解：原式=lim sin2x X lim 3x 3x→0 2x X→0 2x x→0sin3x 2-3 2x lim sin2x =1×1× 3 2x 2-3 X→0 号×1 3 =

(3) 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟑𝒙 解：原式= 𝟏 𝟑 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 ×2 = 𝟐 𝟑 × 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 = 𝟐 𝟑 ×1=𝟐 𝟑 (4) 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝒔𝒊𝒏𝟑𝒙 解：原式= 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 × 𝒍𝒊𝒎 𝒙→𝟎 𝟑𝒙 𝒔𝒊𝒏𝟑𝒙 × 𝟐 𝟑 = 𝟏 ×1 × 𝟐 𝟑 = 𝟐 𝟑

函数极限与连续 练习： (1)lim sin4x=(A) 3 3x A号 C:1 X-→0 2x=(C) (2)4stn A B:2 C:1 3)gx=（D） A:0B:4 C:1 D

练习： (1) 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟒𝒙 𝟑𝒙 = （ ） (2) 𝒍𝒊𝒎 𝒙→𝟎 𝟐𝒙 𝒔𝒊𝒏𝟐𝒙 = （ ） (3) 𝒍𝒊𝒎 𝒙→𝟎 𝒙 𝒔𝒊𝒏𝟒𝒙 = （ ） A:𝟒 𝟑 B:𝟑 𝟒 C:𝟏 D:𝟏 𝟒 A:𝟏 𝟐 B:𝟐 C:𝟏 D:𝟏 𝟒 A:0 B:𝟒 C:𝟏 D:𝟏 𝟒 A C D

函数极限与连续 分析： 1类型：型 2.变形： lim x二1 x→0sinx 3.形似： limsinu 二1 u→02u 故： lim =1osr西 f(x)=1 f(x-o f(x) 4.推广：limn= lim sinx =lim sinx =1 x→0 x→0xc0Sx x→0x lim tanf()=1,lim fx二1 f(x)0 f(x) f(x)0 tanf(x)

分析： 1.类型：𝟎 𝟎 型 2.变形： 𝒍𝒊𝒎 𝒙→𝟎 𝒙 𝒔𝒊𝒏𝒙 = 𝟏 3.形似： 𝒍𝒊𝒎 𝒖→𝟎 𝒔𝒊𝒏𝒖 𝒖 = 𝟏 故： 𝒍𝒊𝒎 𝒇(𝒙)→𝟎 𝒔𝒊𝒏𝒇(𝒙) 𝒇(𝒙) = 𝟏, 4.推广： 𝒍𝒊𝒎 𝒙→𝟎 𝒕𝒂𝒏𝒙 𝒙 = 𝒍𝒊𝒎 𝒇(𝒙)→𝟎 𝒕𝒂𝒏𝒇(𝒙) 𝒇(𝒙) = 𝟏, 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝒙 𝒙𝒄𝒐𝒔𝒙 =𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝒙 𝒙 = 𝟏 𝒍𝒊𝒎 𝒇(𝒙)→𝟎 𝒇(𝒙) 𝒕𝒂𝒏𝒇(𝒙) = 𝟏 𝒍𝒊𝒎 𝒇(𝒙)→𝟎 𝒇(𝒙) 𝒔𝒊𝒏𝒇(𝒙) = 𝟏

函数极限与连续 sin2x (6)lim sin2x (5)lim x→0tan3x x0cos3x 解：原式=lim sin2x、 3x 分母不为零，直接代入。 X→0 2x tan3x 2-3 2 sin2x 3x 解：原式=lim sinc ×0 ×lim x-0 coso 2x x→0tan3x =9=0 =号×1×1=号 因为c0s0=1

(5) 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝒕𝒂𝒏𝟑𝒙 解：原式= 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 × 𝟑𝒙 𝒕𝒂𝒏𝟑𝒙 × 𝟐 𝟑 = 𝟐 𝟑 × 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝟐𝒙 × 𝒍𝒊𝒎 𝒙→𝟎 𝟑𝒙 𝒕𝒂𝒏𝟑𝒙 = 𝟐 𝟑 ×1× 𝟏= 𝟐 𝟑 (6) 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟐𝒙 𝒄𝒐𝒔𝟑𝒙 分母不为零，直接代入。 解：原式= 𝒍𝒊𝒎 𝒙→𝟎 𝒔𝒊𝒏𝟎 𝒄𝒐𝒔𝟎 = 𝟎 𝟏 =𝟎 因为cos𝟎 = 𝟏