《高等数学》课程教学课件（讲稿）2-4-2无穷大量

第五讲 无穷大与无穷小

函数极限与连续 第五讲 无穷大与无穷小

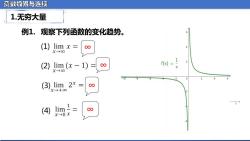
函极限与连续 1.无穷大量 例1.观察下列函数的变化趋势。 (1) limx= X→00 1 (2)1 im(x-1)=∞ f(x)= X→00 -0 (3)lim 2x 00 X→+00 (4 lim= 00 X→0X

函数极限与连续 例1. 观察下列函数的变化趋势。 (1) (2) (3) ∞ ∞ ∞ (4) ∞ 1.无穷大量

函数极限与连续 1.无穷大量 定义1 若当x一x0(或x一→o∞)时，函数f(x)的 绝对值无限增大则称f(x)是x→x(或x→∞)的 无穷大量，简称无穷大。 说明：(1)说函数是无穷大，须指明自变量的变化趋势； (2)绝对值很大的常数不是无穷大； (3)“∞”只是一种记法，此时函数的极限 不存在

函数极限与连续 定义1 ： 说明： (1) 说函数是无穷大，须指明自变量的 变化趋势； (3) “∞ ”只是一种记法，此时函数的极限 不存在。 (2) 绝对值很大的常数不是无穷大； 1.无穷大量

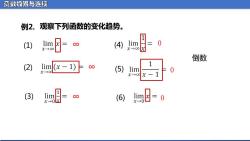
函叙极限与连续 例2.观察下列函数的变化趋势。 (1) (4) lim =0 X→00 倒数 (2) [x-1)∞ (5)1im 0 X→00 (3) 目。日-0

函数极限与连续 (1) (2) (3) ∞ (4) (5) (6) 0 ∞ ∞ 0 0 例2. 观察下列函数的变化趋势。 倒数

函数极限与连续 2无穷大与无穷小的关系 定理2在自变量的同一变化过程中， 如果f(田为无穷大，则是无穷小 如果f(x)为无穷小，且f(x)≠0， 则 是无穷大

函数极限与连续 定理2 ： 在自变量的同一变化过程中， 2.无穷大与无穷小的关系

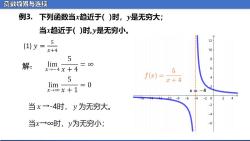
函数极限与连续 例3.下列函数当x趋近于()时，y是无穷大： 当x趋近于()时，y是无穷小。 (1)y= 5 12 X+4 10 5 解： lim 三00 x-4X+4 5 6 5 f(x)= x+4 A lim =0 x∞X+1 X÷一4 -8 6 -20 当x→-4时，y为无穷大。 -2 当x→o时，y为无穷小；

函数极限与连续 例3. 解：

丞数极限与连续 (2)y= x+5 x+4 x+5 解：lim 三00 - x→-4X+4 x+5 f(x)= x+5 x-4 lim =0 2 x-5X+4 X日-4 当x→-4时，y为无穷大。 -8 -6 44 -2 0 当x→-5时，y为无穷小 -2

函数极限与连续 解：

函数极限与连续 练习：下列函数当x趋近于()时，y是无穷小； 当x趋近于()时，y是无穷大。 0y2 当x→（4)时，y为无穷大。 当x→（∞)时，y为无穷小； x+6 (2)y=x-3 当x→（3)时，y为无穷大。 当x→（-时，y为无穷小；

函数极限与连续 当x→ （ ）时，y为无穷小； 当x→（ ）时，y为无穷大。 当x→ （ ）时，y为无穷小； 当x→（ ）时，y为无穷大。 4 ∞ 3 − 6

函数极限与连续 练习：下列函数当x趋近于()时，y是无穷小； 当x趋近于()时，y是无穷大。 (3)y 当x→（2)时，y为无穷大。 当x→（7)时，y为无穷小； (④y 当x→（1)时，y为无穷大。 当x→（∞)时，y为无穷小

函数极限与连续 当x→ （ ）时，y为无穷小； 当x→（ ）时，y为无穷大。 当x→ （ ）时，y为无穷小. 当x→（ ）时，y为无穷大。 2 7 1 ∞

函极限与连续 课堂小结 “∞”只是一种记法，此时函数的极限不存在。 无穷大量 在自变量的同一变化过程中， 如果f(x)为无穷大，则是无穷小 f(x) 如果f()为无穷小，且f(x0,则是无穷大

函数极限与连续 课堂小结 无穷大量 “ ∞ ”只是一种记法，此时函数的极限不存在。 在自变量的同一变化过程中