《高等数学》课程教学资源（PPT课件）反常积分

山东农业大 兰 主进 方本堂 第四节 反常积分 、无穷限的反常积 分 二、无界函数的反常积分

山东农业大学 高等数学 主讲人：苏本堂 第四节 反常积分 一、无穷限的反常积 分 二、无界函数的反常积分

积分限有限 常义积分 被积函数有界 解决许多实际问题要求我们将函数x)从有限区间 推广到无限区间，将有界函数推广到无界函数.从而得到 两种反常积分（也称广义积分）

山东农业大学 高等数学 主讲人：苏本堂 常义积分 积分限有限 被积函数有界 解决许多实际问题要求我们将函数f(x)从有限区间 推广到无限区间,将有界函数推广到无界函数.从而得到 两种反常积分(也称广义积分)

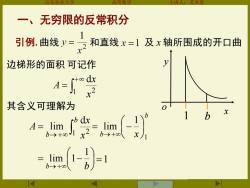
方本 一、 无穷限的反常积分 1 引例.曲线y=2和直线x=1及x轴所围成的开口曲 边梯形的面积可记作 a= r+co dx x2 其含义可理解为 1停 lim b-→+0(

山东农业大学 高等数学 主讲人：苏本堂 一、无穷限的反常积分 引例. 曲线 和直线 及 x 轴所围成的开口曲 边梯形的面积 可记作  + = 1 2 d x x A 其含义可理解为  →+ = b b x x A 1 2 d lim b b x 1 1 lim       = − →+       = − b→+ b 1 lim 1 =1 1 b y o x

定义1.设f(x)∈C[a,+oo),取b>a,若 mfowdr b->t 存在，则称此极限为f(x)的无穷限反常积分，记作 。fx)dx=,imjf)dr 这时称反常积分∫f(x)dx收敛；如果上述极限不存在， 就称反常积分∫f()d发散. 类似地，若f(x)∈C(-0,b],则定义 ∫fcxd=lim)dr

山东农业大学 高等数学 主讲人：苏本堂 定义1.设 f (x)C[a, + ), 取b  a, 若 存在 , 则称此极限为f (x) 的无穷限反常积分, 记作 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . 类似地 , 若 f (x)C(−, b], 则定义

本 若f(x)∈C(-o,+o),则定义 ∫f)d=mgf)dx+mi/e)d (c为任意取定的常数) 只要有一个极限不存在，就称f(x)dr发散. 无穷限的反常积分也称为第一类反常积分 说明：上述定义中若出现∞-∞，并非不定型， 它表明该反常积分发散

山东农业大学 高等数学 主讲人：苏本堂 若 f (x)C(−, + ), 则定义 f x x c a a lim ( )d  →− f x x b b c lim ( )d  →+ + ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 . 无穷限的反常积分也称为第一类反常积分. 说明: 上述定义中若出现  −  , 并非不定型 , 它表明该反常积分发散

若F(x)是f(x)的原函数，引入记号 F(+co)=lim F(x);F(-oo)=lim F(x) 则有类似牛一莱公式的计算表达式： (F)-F(a) d=re2=F0-F网 F)F)

山东农业大学 高等数学 主讲人：苏本堂 引入记号 F( ) lim F(x) ; x→+ + = F( ) lim F(x) x→− − = 则有类似牛 – 莱公式的计算表达式 : f x x a ( )d  + = F(x) = F(+) − F(a) f x x b ( )d − = F(x) = F(b) − F(−) f (x)dx  + − = F(x) = F(+) − F(−)

方本堂 dx 1.计算反常积分悦 解1=1aea 1+x2 a b 思考：关0对吗？ 分标：=n0+2) +0 原积分发散！ 注意：对反常积分，只有在收敛的条件下才能使用 “偶倍奇零”的性质否则会出现错误

山东农业大学 高等数学 主讲人：苏本堂 例1. 计算反常积分 解: + − = [arctan x] ) 2 (  − − 2  = = 思考: 分析: 原积分发散 ! 注意: 对反常积分, 只有在收敛的条件下才能使用 “偶倍奇零”的性质否则会出现错误 ,

例2.讨论反常积分 xP 的敛散性 解：当p=1时有 E=[lnx]2=+∞ 当p≠1时有 - +0, p1 p-1 al-p 因此，当p>1时，反常积分收敛，其值为 p-1 当p≤1时，反常积分发散

山东农业大学 高等数学 主讲人：苏本堂 例2. 讨论反常积分 解:当 p =1 时有   + = a ln x = + − +    −  = a p p x 1 1 当 p ≠ 1 时有 p 1 , p 1 1 1 − − p a p 的敛散性. +  , 因此, 当 p >1 时, 反常积分收敛, 其值为 ; 1 1 − − p a p 当 p≤1 时, 反常积分发散

例3.计算反常积分te pidi(p>0) 解原式-e。 1 +00 0

山东农业大学 高等数学 主讲人：苏本堂 例3. 计算反常积分 解: pt e p t − 原式 = −  + − + 0 d 1 e t p pt pt e p − = − 2 1 2 1 p =

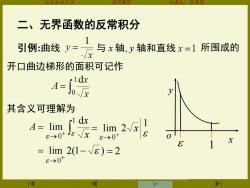
二、无界函数的反常积分 引例：曲线y=↓ 与x轴，y轴和直线x=1所围成的 x 开口曲边梯形的面积可记作 4 其含义可理解为 4m儿指期2 =lim2(1-W8)=2 8→0

山东农业大学 高等数学 主讲人：苏本堂 二、无界函数的反常积分 引例:曲线 与 x 轴, y 轴和直线 所围成的 开口曲边梯形的面积可记作 其含义可理解为 +  → = 1 0 d lim   x x A   1 lim 2 0 x → + = lim 2(1 ) 0   = − → + = 2  1 y o x