《高等数学》课程教学资源（PPT课件）数列的极限

、本 第二节 数列的极限 数列极限的定义 二、收敛数列的性质

山东农业大学 高等数学 主讲人： 苏本堂 第二节 数列的极限 一、 数列极限的定义 二、 收敛数列的性质

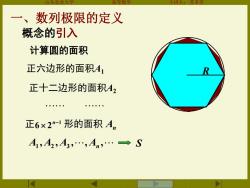
一、 数列极限的定义 概念的引入 计算圆的面积 正六边形的面积A1 正十二边形的面积A2 。 。● 正6×2-1形的面积An A1,A2,A3,.,An,.→S

山东农业大学 高等数学 主讲人： 苏本堂 一 、数列极限的定义 概念的引入 正六边形的面积A1 R   正6  2 n1 形的面积 An A1 , A2 , A3 ,, An , S 正十二边形的面积A2 计算圆的面积

山东衣 1.数列的概念 按照某一法则，对每一neN+,对应着一个确定的实数 x则得到一个序列 X1X22X3)···,Xn· 这一序列叫做数列，记为{xn},第n项xn叫做数列的一般项， 2,4,82·,2n,.;1,-1,1,.,（-1)+1,. 1111 2'4'82, 24n+ 2’3’ 注意：(1)数列对应着数轴上一个点列.可看作一动 点在数轴上依次取X1,X2).,Xn,. X3x1 X2x4 n (2).数列是整标函数xn=f(n),n∈N+

山东农业大学 高等数学 主讲人： 苏本堂 1. 数列的概念 按照某一法则, 对每一nN , 对应着一个确定的实数 xn , 则得到一个序列 x1 , x2 , x3 ,    , xn ,    , 这一序列叫做数列, 记为{xn}, 第n项xn叫做数列的一般项. 2, 4, 8,    , 2 n ,    ; 1, 1, 1,    , (1)n1 ,    . , ; 2 1 , , 8 1 , 4 1 , 2 1  n  , ; ( 1) , , 3 4 , 2 1 2, 1   n n n   注意： (1).数列对应着数轴上一个点列.可看作一动 点在数轴上依次取 , , , , . x1 x2  xn  1 x 2 x 3 x 4 x n x (2).数列是整标函数 x f (n), n  .  n N

观察数列+)二)当n→0时的变化趋势 n 通过观察：当n无限增大时，=1+) 无限接近于1 问题：“无限接近”意味着什么？如何用数学语言刻划它 x。-1=(-1)=1 给定 由11 n100时，有x-110000时，有x.-10，只要n>N(=时，有x,-1<ε成立

山东农业大学 高等数学 主讲人： 苏本堂 问题:“无限接近”意味着什么?如何用数学语言刻划它. 通过观察:当n无限增大时, n x n n 1 ( 1) 1     无限接近于1. 引例 观察数列 } ( 1) {1 1 n n   当n   时的变化趋势. , 100 1 给定 , 100 1 1  n 由 只要 n  100时, , 100 1 有 xn  1  , 10000 1 , 有 xn  1  10000 1 给定 只要 n  10000时, 给定   0, ]) , 1 只要 ( [ 时  n  N  有  1  成立. n x  xn  1  n n n 1 1 ( 1) 1   

2.数列极限的通俗定义 当n无限增大时，如果数列{xm}的一般项xn无限接近 于常数a,则常数a称为数列{x,}的极限，或称数列{xn}收 敛a,记为 lim x=a 当n无限增大时，xn无限接近于a. 一当n无限增大时，xma无限接近于0 →当n无限增大时，xna可以任意小，要多小就能有多小 一当n增大到一定程度以后，nad能小于事先给定的任意 小的正数 因此，若n增大到一定程度以后，x,a能小于事先给 定的任意小的正数，则当n无限增大时，xn无限接近常数a

山东农业大学 高等数学 主讲人： 苏本堂 2. 数列极限的通俗定义 当n无限增大时, 如果数列{xn}的一般项xn无限接近 于常数a, 则常数a称为数列{xn}的极限, 或称数列{xn}收 敛a, 记为 xn a n   lim . 当n无限增大时, xn无限接近于a . 当n无限增大时, |xn-a|无限接近于0 . 当n无限增大时, |xn-a|可以任意小, 要多小就能有多小. 当n增大到一定程度以后, |xn-a|能小于事先给定的任意 小的正数. 因此, 若 n 增大到一定程度以后, |xn-a|能小于事先给 定的任意小的正数, 则当n无限增大时, xn无限接近常数a

3.数列极限的精确定义 设{x,n}为一数列，如果存在常数a,对于任意给定的正 数s,总存在正整数N,使得当>N时，不等式 xm-a长e 都成立，则称常数a是数列{x}的极限，或者称数列{xn}收 敛于a,记为 limx=a或 xn→a(n→o) n-→oo 如果数列没有极限，就说数列是发散的.习惯上也说 limx不存在 n→o 极限定义的简记形式 limx=a→Hε>0,3NeN+,当>N时，有Kn-d<e. n→0

山东农业大学 高等数学 主讲人： 苏本堂 3. 数列极限的精确定义 设{xn}为一数列, 如果存在常数a, 对于任意给定的正 数 , 总存在正整数N, 使得当n>N 时, 不等式 |xna |< 都成立, 则称常数a是数列{xn}的极限, 或者称数列{xn}收 敛于a, 记为 lim n n x a   或 (n ) n x  a   如果数列没有极限,就说数列是发散的. 习惯上也说 lim n n x  不存在 极限定义的简记形式  0, NN , 当nN时, 有|x lim na| . n n x a  

注： (I).e的任意性，它是描述xn与a的无限接近程度 (2).N与ε有关，但不唯一 (3)几何解释： 28 a-E a+8 X2 X1 XN+I XN+2 当n>N时，所有的点xn都落在开区间(a-6,a+8),只有 有限个（至多只有N个）落在这区间以外 (4)数列极限的定义未给出求极限的方法

山东农业大学 高等数学 主讲人： 苏本堂 注： (1). 的任意性，它是描述xn 与a 的无限接近程度. (2). N 与ε有关，但不唯一. (3) 几何解释: x 1 x 2 x N 2 x N 1 x 3 x 2 a   a   a (4).数列极限的定义未给出求极限的方法. 当 n>N 时,所有的点xn 都落在开区间(a-,a+) ,只有 有限个(至多只有N个)落在这区间以外

山」 例1证明 lim (1) =1. 11-→c∞ n 证明 Ve>0,取N=h, 则当心>N时，就有 n 即lim +)=1. n-→c0 n 分析 n+1-1 1 对于任意&>0，要使x-l1 n

山东农业大学 高等数学 主讲人： 苏本堂 证明 例1 证明 1. ( 1) lim 1      n n n n 对于任意 >0,要使|xn-1|N 时,就有       1 ( 1) 1 n n n 1. ( 1) lim 1      n n n n 即

等数 例2证明 (-1)” limx=lim =0 n→00 →∞(n+1)2 证明V8>0取N=已-1]，则当>N时，就有 k.-a- 1 1 0,(设e-1

山东农业大学 高等数学 主讲人： 苏本堂 例2 证明 n 2 ( 1) lim lim 0. ( 1) n n n x   n    分析 证明 xn  a 0 ( 1) ( 1) 2     n n 2 ( 1) 1   n . 1 1   n   0, (设  1 ), 要使 , 1 1   n  或 1, 1    n | xn  a |  , 只要   0, 1 N [ 1],  取   则当n>N 时,就有 xn  a 2 ( 1) 1   n 1 . n 1     所以 0. ( 1) ( 1) lim 2     n n n

例3设1qk1,证明等比数列 1,9,q2,·,q-1,· 的极限是0. 证明ye>uN-H号 则当>N时，就有 l,-ol=lal0,要使|xn-aK6,只要gm-11+ ng

山东农业大学 高等数学 主讲人： 苏本堂 例3 设|q|N 时,就有 ln [1 ], ln N q  取   1 0 . n n x q      所以 lim 0. 1    n n q