《高等数学》课程教学资源（PPT课件）6.4 第六章习题课

率数学 本堂 第六章习题课 1.定积分的应用 几何方面：面积、体积、弧长、表面积 物理方面：质量、作功、侧压力、引力、 2.基本方法微元分析法 微元形状：条、段、带、片、扇、环、壳等

山东农业大学 高等数学 主讲人：苏本堂 第六章习题课 1. 定积分的应用 几何方面 :面积、体积、弧长、表面积 . 物理方面 :质量、作功、侧压力、引力、 2. 基本方法 微元分析法 : 微元形状 :条、段、带、片、扇、环、壳 等

典型例题 例1 1) 已知 星形线 (a>0) 0 0 y=asin3 t 求1°它所围成的面积； 2°它的弧长： 3它绕x轴旋转而成的旋转体 体积及表面积

山东农业大学 高等数学 主讲人：苏本堂 例1 3 3 0 0 0 cos ( 0) sin 1 ; 2 ; 3 . x a t a y a t  =    = 已知 星形线 求 它所围成的面积 它的弧长 它绕x轴旋转而成的旋转体 体积及表面积 − a a o y x 典型例题

方本堂 解1°设面积为A.由对称性，有 A=4 asint.3acos -sint)dt =1ri水dn-sinw-a2 2°设弧长为L.由对称性，有 dt=f3acostsintdt =6a

山东农业大学 高等数学 主讲人：苏本堂 解 1 . 0 设面积为 A 由对称性,有  = a A ydx 0 4 =   − 0 2 3 2 4 asin t 3acos t( sin t)dt   = − 2 0 2 4 6 12 a [sin t sin t]dt . 8 3 2 = a 2 . 0 设弧长为 L 由对称性,有   =  +  2 0 2 2 L 4 (x ) ( y ) dt   = 2 0 4 3acostsin tdt = 6a

3设旋转体的表面积为S,体积为V. 由对称性，有 S=2"2my+d =4n asint.3acostsintdt 22. 5 V=2dx =2xa'sin't.3acos't-sint)dr -Gxa fsin'(1-sin'()dt -2 a3. 05

山东农业大学 高等数学 主讲人：苏本堂 3 , . 0 设旋转体的表面积为 S 体积为V 由对称性,有  =  +  a S y yx dx 0 2 2 2 1   =   2 0 3 4 asin t 3acostsin tdt . 5 12 2 = a  =  a V y dx 0 2 2 =    − 0 2 2 6 2 2 a sin t 3acos t( sin t)dt   =  − 2 0 3 7 2 6 a sin t(1 sin t)dt . 105 32 3 = a

苏本堂 例2.求抛物线y=1-x2在(0,1)内的一条切线，使它与 两坐标轴和抛物线所围图形的面积最小. 解：设抛物线上切点为M(x,1-x2) 则该点处的切线方程为 Y-1-x2)=-2x(X-x) 它与x,y轴的交点分别为 A(,0),B(0,x2+1) 所指面积 500-号-ar-号 4x

山东农业大学 高等数学 主讲人：苏本堂 例2. 求抛物线 在(0,1) 内的一条切线, 使它与 两坐标轴和抛物线所围图形的面积最小. 解: 设抛物线上切点为 则该点处的切线方程为 它与 x , y 轴的交点分别为 所指面积 M B A

S(=2+1)-3r2-1) 令S"(x)=0,得[0,1]上的唯一驻点x= x号，S(>0 因此x=5是S()在[0，川上的唯一极小点， 且为最小点.故所求切线为 Ps 2/34 X+ 3 3 D

山东农业大学 高等数学 主讲人：苏本堂 且为最小点 . 故所求切线为 得[ 0 , 1] 上的唯一驻点 M B A

例3.设非负函数f(x)在[0,1]上满足x'(x)=f(x) +92,曲线y=f)与直线x=1及坐标轴所围图形 面积为2， (1)求函数f(x); (2)α为何值时，所围图形绕x轴一周所得旋转体 体积最小？ 解：(1)当x≠0时，由方程得 0即1- x2 3 故得 f(x)-2@x2+Cx

山东农业大学 高等数学 主讲人：苏本堂 例3. 设非负函数 曲线 与直线 及坐标轴所围图形 (1) 求函数 (2) a 为何值时, 所围图形绕 x 轴一周所得旋转体 解: (1) 由方程得 面积为 2 , 体积最小 ? 即 故得

2-ed-=j3aw2ad=号* >C=4-a 一f)-r2+4-o (2)旋转体体积 -a40刘 令r-a+10=0,得a=-5 又 ya=-5 π >0, 15 ∴.a=-5为唯一极小点，因此a=-5时V取最小值

山东农业大学 高等数学 主讲人：苏本堂 又 (2) 旋转体体积 又 为唯一极小点,因此 时 V 取最小值 . x o y 1 x o y 1

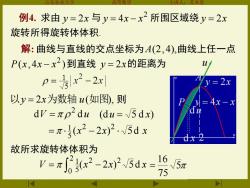
例4.求由y=2x与y=4x-x2所围区域绕y=2x 旋转所得旋转体体积. 解：曲线与直线的交点坐标为A(2,4),曲线上任一点 P(x,4x-x2)到直线y=2x的距离为 p=52-2x 2x 以y=2x为数轴u(如图，则 dV=πp2dw(du=√5dx) =π(x2-2x)2.5dx 】 故所求旋转体体积为 V=a63(x2-225dx=165a 75

山东农业大学 高等数学 主讲人：苏本堂 y = 2x 2 y = 4x − x o (du = 5 d x) 故所求旋转体体积为 (x 2x) 5d x 2 2 5 1 =   −  5 75 16 V (x 2x) 5d x = 2 2 2 0 5 1 = −   dV du 2 =   A P d x 2 du 例4. 求由 y = 2x 与 2 y = 4x − x 所围区域绕 y = 2x 旋转所得旋转体体积. 解: 曲线与直线的交点坐标为 A(2,4), 曲线上任一点 ( ,4 ) 2 P x x − x 到直线 y = 2x 的距离为 以y = 2x为数轴 u (如图), u 则

例5.半径为R,密度为P的球沉入深为H(H>2R) 的水池底，水的密度Po<p,现将其从水池中取出，需做 多少功？ 解：建立坐标系如图.则对应[x,x+dx] 上球的薄片提到水面上的微功为 dwi=(p-Po)gxy2 dx-(H-R+x) =(p-Po)gz(R2-x2)(H-R+x)dx 提出水面后的微功为 微元体积 dW2=pgπy2dx(R-x) 所受重力 =pgπ(R2-x2R-x)dx 上升高度 (x,y)

山东农业大学 高等数学 主讲人：苏本堂 例5. 半径为 R , 密度为 的球沉入深为H ( H > 2 R ) 的水池底, 水的密度 多少功 ? 解: 建立坐标系如图 .则对应 [x, x + dx] 上球的薄片提到水面上的微功为 dW1 = y dx 2  提出水面后的微功为 dW2 g d ( ) 2 =   y x  R − x g (R x )(R x)dx 2 2 =   − − ( )g (R x )(H R x)dx 2 2 =  − 0  − − + H (x, y) x x y o 现将其从水池中取出, 需做 微元体积 所受重力 上升高度 ( − 0 )g (H − R + x)