内蒙古科技大学：《材料力学》课程PPT教学课件（材料、成型、矿物）第11章 能量方法

材料力学第十一章能量方法

第十一章能量方法变形能的普遍表达式$11-1$11-2莫尔定理（单位力法811-3截面上的应力及强度条件

第十一章 能量方法 §11–1 变形能的普遍表达式 §11–2 莫尔定理(单位力法) §11–3 截面上的应力及强度条件

能量方法811-12变形能的普遍表达式能量原理：弹性体内部所贮存的变形能，在数值上等于外力所作的功，即U-W利用这种功能关系分析计算可变形固体的位移、变形和内力的方法称为能量方法二、杆件变形能的计算：1.轴向拉压杆的变形能计算：2N')dx 或u-ZNLU=[ 4比能:u-08-12E,A22EA

§11–1 变形能的普遍表达式 一、能量原理： 二、杆件变形能的计算： 1.轴向拉压杆的变形能计算：  = L x EA N x U d 2 ( ) 2 = = n i i i i i E A N L U 1 2 2 或  2 1 比能: u = 弹性体内部所贮存的变形能，在数值上等于外力所作 的功，即 U=W 利用这种功能关系分析计算可变形固体的位移、变形 和内力的方法称为能量方法

能量方法2.扭转杆的变形能计算：M.(x)喜.dxU-r或U=T2GIp1比能:u一TY23. 弯曲杆的变形能计算:M(x)或U-u-I.dx2EI1比能:u=082

2.扭转杆的变形能计算：  = L P n x GI M x U d 2 ( ) 2 = = n i i Pi ni i G I M L U 1 2 2 或  2 1 比能: u = 3.弯曲杆的变形能计算：  = L x EI M x U d 2 ( ) 2 = = n i i i i i E I M L U 1 2 2 或  2 1 比能: u =

能量方法三、变形能的普遍表达式变形能与加载次序无关；相互独立的力（矢）引起的变形能可以相互叠加。U-I N()dx+ [ M()dx+M(x)dx2EA2GIp2EI(x) dx+J. asαs >剪切挠度因子2EA细长杆，剪力引起的变形能可忽略不计。M'(x)dxr N'(x)dx +M(x)dx+公一2EAT2EI2GIp

三、变形能的普遍表达式： 变形能与加载次序无关；相互独立的力（矢）引起的变形能 可以相互叠加。 细长杆，剪力引起的变形能可忽略不计。  + L x EA Q x d 2 ( ) 2 S S → 剪切挠度因子x EI M x x GI M x x EA N x U L L P n L d 2 ( ) d 2 ( ) d 2 ( ) 2 2 2    = + + x EI M x x GI M x x EA N x U L L P n L d 2 ( ) d 2 ( ) d 2 ( ) 2 2 2    = + +

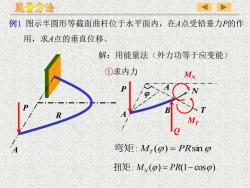
能量方法例1图示半圆形等截面曲杆位于水平面内，在A点受铅垂力P的作用，求A点的垂直位移。解：用能量法（外力功等于应变能）①求内力MNRM.7弯矩:M,(β)=PRsin A扭矩:M (β)= PR(1-cosβ)

Q MN MT A A P N B j T 例1 图示半圆形等截面曲杆位于水平面内，在A点受铅垂力P的作 用，求A点的垂直位移。 解：用能量法（外力功等于应变能） ①求内力 弯矩: MT (j) = PRsinj : M (j) = PR(1− cosj) 扭矩 N A P R

能量方法②变形能：dx12EA2E1PRa-oso)Rdo+PRsn)Rdo元Jo2GIp2EIP2R元3P2R元4GIp4EI③外力功等于应变能3PR元PR元P:. f4.W.f=U2EI2GIp2

③外力功等于应变能 ②变形能：    = + + L L P L x EI M x x G I M x x EA N x U d 2 ( ) d 2 ( ) d 2 ( ) 2 2 n 2   + − =   j j j j 0 2 2 2 0 2 2 2 d 2 (sin ) d 2 (1 cos ) R EI P R R GI P R P EI P R GI P R 4 P 4 3 2 3 2 3   = + f U P W = A = 2  EI PR GI PR f P A 2 2 3 3 3    = +

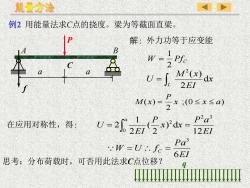
能量方法例2用能量法求C点的挠度。梁为等截面直梁A解：外力功等于应变能PBLA1SPrW=RA2M(x) dxU-I.2EIAM(x) =*;(0≤≤a)PaL(Px)dx=U = 2]。.2F在应用对称性，得：2.EI212EIPa3w-U..fc -16EI思考：分布荷载时，可否用此法求C点位移？q

例2 用能量法求C点的挠度。梁为等截面直梁。 W PfC 2 1 = 解：外力功等于应变能  = L x EI M x U d 2 ( ) 2 ;(0 ) 2 ( ) x x a P M x =   在应用对称性，得： EI P a x x P EI U a 12 ) d 2 ( 2 1 2 2 3 0 2 = =  EI Pa W U f C 6 3  =  = 思考：分布荷载时，可否用此法求C点位移？ q C a a A P B f

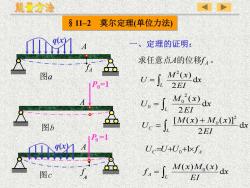
能量方法$11-2莫尔定理（单位力法）定理的证明：V求任意点A的位移f，HfHMe(x) dx图aU-J.[Po=12EIM(x) dxU。-J.2EI.R[M(x)+ M.(x))dxUc=图b2EIP=1g(VUc-U+U.+Ixfa8M(x)M.(x) dxL-J 44图cEI

§11–2 莫尔定理(单位力法) C A U =U+U +1f 0  = L x EI M x U d 2 ( ) 2  = L x EI M x U d 2 ( ) 2 0 0  + = L C x EI M x M x U d 2 [ ( ) ( )]2 0  = L A x EI M x M x f d ( ) ( ) 0 求任意点A的位移f A 。 一、定理的证明： a A 图 fA q(x) 图c A P0 =1 q(x) f A 图b A P0=1

能量方法 M(x)M.()dx莫尔定理(单位力法）二EI一、普遍形式的莫尔定理.-I N(N()ax+J M(M(a+ I M()M()ax1EIEAGI

莫尔定理(单位力法) 二、普遍形式的莫尔定理 x EI M x M x f L A d ( ) ( ) 0  =   = + + L P n n L A x GI M x M x x EA N x N x d ( ) ( ) d ( ) ( ) 0 0  x EI M x M x L d ( ) ( ) 0 