内蒙古科技大学：《材料力学》课程PPT教学课件（材料、成型、矿物）附录——截面的几何性质

材料力学附录I截面的几何性质

附录I截面的几何性质附录IS1-1面积矩与形心位置附录I81-2惯性矩、惯性积、极惯性矩附录I81-3惯性矩和惯性积的平行移轴定理附录181-4惯性矩和惯性积的转轴定理*截面的主惯性轴和主惯性矩

附录I§1–1 面积矩与形心位置 附录I§1–2 惯性矩、惯性积、极惯性矩 附录I§1–3 惯性矩和惯性积的平行移轴定理 附录I 截面的几何性质 附录I§1–4 惯性矩和惯性积的转轴定理* 截面的主惯性轴和主惯性矩

附录附录I81-1面积矩与形心位置一、面积（对轴）矩：（与力矩类似）是面积与它到轴的距离之积1M0Nm0MMe.TmGI.W.xdS,-dAydAdS,=dAxS.-Jds.-[yd41S,-[ds,-[xd4

附录 I§1-1 面积矩与形心位置 一、面积（对轴）矩：(与力矩类似) 是面积与它到轴的距离之积。 P n P n W M G I M A N max max max max  = ; = ;  = S A y x d =d  S Ax y d =d      = = = = A A y y A A x x S S x A S S y A d d d d dA x y y x

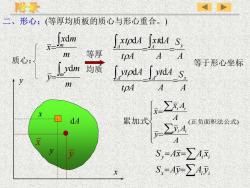
附录二、形心：(等厚均质板的质心与形心重合。)[xdmJ xtpd4[xidA S,Jm4x=等厚mAAtpA质心：等于形心坐标 ydm均质J,ytpdA[ ytdASyJmV=1 ymAAtpAZxAXxAdA累加式（正负面积法公式）ZyAyAx1S,=Ax-Ax1S=-Ay-LAJ,x

二、形心：(等厚均质板的质心与形心重合。) 累加式: (正负面积法公式)        = =   A y A y A x A x i i i i   = = = = x i i y i i S Ay A y S Ax A x dA x y y x 等厚 均质 m y m y m x m x m m   = = d d 质心： A S A yt A t A yt A A S A x t A t A x t A A A x A A y = = = =     d d d d     等于形心坐标 x y

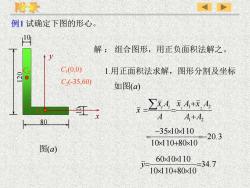
附录例1试确定下图的形心19解：组合图形，用正负面积法解之3C(0,0)1.用正面积法求解，图形分割及坐标00OC2(-35,60)如图(a)x,A_XA+x,A,91AA,+A,8035x10x11020.310x110+80x10图(a)60x10x1 10-34.710x110+80x10

1 2 1 1 2 2 A A x A x A A x A x i i + + =  = 20.3 10 110 80 10 35 10 110 =−  +  −   = 34.7 10 110 80 10 60 10 110 =  +    y= 例1 试确定下图的形心。 解 ： 组合图形，用正负面积法解之。 1.用正面积法求解，图形分割及坐标 如图(a) 80 120 10 10 x y C2 图(a) C1 C1 (0,0) C2 (-35,60)

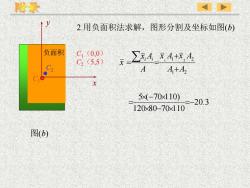
附录12.用负面积法求解，图形分割及坐标如图(b)负面积C (0,0)T_ExA X4+F4C, (5.5)C2AA+A,.CCx5x(-70x110)20.3120x80-70xl 10图(b)

2.用负面积法求解，图形分割及坐标如图(b) 20.3 120 80 70 110 5 ( 70 110) =−  −   −  = 图(b) C1（0,0） C2（5,5） 1 2 1 2 1 2 A A x A x A A x A x i i + + =  = C2 负面积 C1 x y

附录附录I81-2惯性矩、惯性积、极惯性矩惯性矩：（与转动惯量类似）是面积与它到轴的距离的平方之积。I-[y'd4I,-fx'dAxdAA二、极惯性矩：O是面积对极点的二次矩。xI,-[p’dA-I,+1

附录 I§1-2 惯性矩、惯性积、极惯性矩 一、惯性矩：(与转动惯量类似） 是面积与它到轴的距离的平方之积。   = = A y A x I x A I y A d d 2 2 dA x y y x  二、极惯性矩： 是面积对极点的二次矩。 x y A I = A=I +I  d 2  

附录三、惯性积：面积与其到两轴距离之积-[xydAV如果x或y是对称轴，则I-0xdAAx

dA x y y x  三、惯性积：面积与其到两轴距离之积。  = A I xy xydA 如果 x 或 y 是对称轴，则Ixy =0

附录附录181-3惯性矩和惯性积的平行移轴定理平行移轴定理：（与转动惯量的平行移轴定理类似以形心为原点，建立与原坐标轴平行Yc的坐标轴如图x=a+xcdAy-b+y。XAX1.-y'd4-] (ve+b) d4X-J(y&+2byc+b )d4Sxc=Ay。=0I =I c+b?A=I xc+2bSxc+b2 A

附录 I§1-3 惯性矩和惯性积的平行移轴定理 一、平行移轴定理：（与转动惯量的平行移轴定理类似）    = + = + C C y b y x a x 以形心为原点，建立与原坐标轴平行 的坐标轴如图 SxC =AyC =0 I bS b A y by b A y b A I y A xC xC C A C A C A x 2 2 2 2 2 2 ( 2 )d ( ) d d = + + = + + = + =    I x I xC b A 2 = + dA x y y x  a b C xC yC

附录I = c +b?AI,=/ c+a? A注意：C点必须为形心I ,-/ xcc +abAI,=I c+(a+b)2 A

注意: C点必须为形心 I x I xC b A 2 = + I y I yC a A 2 = + I xy =I xCyC +abA I I C a b A 2 = +( + )  